-

北师大初中八年级数学下册直接提公因式因式分解教案
解析:(1)首先提取公因式13,进而求出即可;(2)首先提取公因式20.15,进而求出即可.解:(1)39×37-13×91=3×13×37-13×91=13×(3×37-91)=13×20=260;(2)29×20.15+72×20.15+13×20.15-20.15×14=20.15×(29+72+13-14)=2015.方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.三、板书设计1.公因式多项式各项都含有的相同因式叫这个多项式各项的公因式.2.提公因式法如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种因式分解的方法叫做提公因式法.本节中要给学生留出自主学习的空间,然后引入稍有层次的例题,让学生进一步感受因式分解与整式的乘法是逆过程,从而可用整式的乘法检查错误.本节课在对例题的探究上,提倡引导学生合作交流,使学生发挥群体的力量,以此提高教学效果.

北师大初中八年级数学下册线段的垂直平分线教案
∵∠DAE=∠DAF,∠AED=∠AFD,AD=AD,∴△ADE≌△ADF,∴AE=AF,DE=DF,∴直线AD垂直平分线段EF.方法总结:当一条直线上有两点都在同一线段的垂直平分线上时,这条直线就是该线段的垂直平分线,解题时常需利用此性质进行线段相等关系的转化.三、板书设计1.线段的垂直平分线的性质定理线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段的垂直平分线的判定定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因此本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对线段垂直平分线性质定理的逆定理理解不透彻,还需在今后的教学和作业中进一步进行巩固和提高.
小学美术岭南版五年级下册《第六单元18活动彩车模型》教材教案
1、了解和认识彩车巡游是节庆游艺形式之一。学习并掌握主题型、活动型彩车模型的设计制作方法。 2、在欣赏评述中,感受节庆中的彩车艺术,在探究实践中拓展设计思维,在参与“彩车巡游”的活动中感受成功的快乐。 3、体验彩车制作的科学原理,乐意和同学分工合作,体验节庆彩车巡游和学习成功的乐趣。 围绕个主题,综合利用各种环保材料设计制作美观的活动彩车模型。 彩车整体造型的构思与应用的活动原理。 教师播放视频,再讲述导语,使学生快速进入课堂学习氛围,引起他们的兴趣。(出示ppt) 师:我们先一起来看一段视频吧!从视频中我们可以看到不同的彩车有不同的装饰和特点。 师:在盛大的庆典或节日的游行队伍里,常可以看到色彩缤纷、造型独特的大型彩车,为节日增添了欢乐的气氛,同时很好地体现了一定的主题和思想内容。

小学美术岭南版五年级下册《第六单元18活动彩车模型》教案
教学目标: 一、了解车的类型、结构、功能等,并学会运用多种媒材制作造型美观的车。 二、掌握制作车的基本方法。 三、在实践操作中感受用不同大小、不同形状,不同质地的材料制作车的乐趣和成就感。 四、训练学生积极地动手、动脑,主动参与实践与创造,养成善于思考、细心观察的好习惯,培养协作精神。 教学重点:利用生活中显而易见的材料,制作汽车。 教学难点:车型设计新颖美观,结构合理。 教师用具:电教媒体,教学课件,汽车范作,剪刀,双面胶等。学生用具:自备的制作汽车的各种材料(如,塑料瓶,易拉罐,各种蔬菜、瓜果,橡胶泥,剪刀,小刀,钻子,牙签,旧鞋,袜子,玩具赛车车轮等。) 教学过程: 一、开门见山,明确目标 1、欣赏萝卜汽车和拖鞋汽车,并分析其制作材料的特殊性。 2、板书课题。 二、交流讨论,呈现问题 1、提出问题,学生讨论:你会选用哪些材料,制作汽车的哪个部分呢? 2、师生互动探讨:恰当、巧妙地选材。(了解学生的创作想法与思路,教师及时予以引导。)

部编人教版六年级上册《盼》说课稿(二)
一、说教材 《盼》是统编教材小学语文六年级上册第五单元地第二篇课文,作者是当代女作家铁凝。课文主要讲地是妈妈给“我”买了一件新雨衣,从那以后,“我”每天总是盼着下雨。一天放学后,终于掉了雨点儿,“我”想出各种借口想穿上雨衣到街上去,都没有实现。第二天早晨,“我”背着书包上街,突然掉下了雨点儿。“我”兴奋地跑回家让妈妈帮“我”穿上新雨衣,走在街上,滴答地雨滴让“我”欣喜不已。课文用生动、准确地语言,恰如其分地表达了想要穿上雨衣地“我”对雨天地渴盼、穿着雨衣在在街上行走地快乐。课文为我们呈现了一幅美好地童年生活画面,文中“我”心底地渴盼更能触动孩子们地心灵。同时,文中运用地多种描写方法也能让学生在习作上受到启发。 二、说教学目标 1.会写12个生字,会写“雨衣、袖筒、斗篷”等 词语。 2.能把握课文内容,知道文章是通过哪些事例来写“盼”地。
初中生物北师大版七年级下册《第14章第1节人类活动对生物圈的影响》教案
知识和技能 1.了解人类活动对生物圈影响的几个方面的实例。 2.掌握环境污染的产生及危害。 3.举例说明人类对生物圈中资源的合理利用。 过程与方法 1.能初步学会收集资料,养成良好的学习习惯,能够运用所学知识、技能分析和解决一些身边的生物学问题的能力。 2.培养学生初步具有近一步获取课本以外的生物学信息的能力。 情感、态度与价值观 1.让学生认识到环境保护的重要性,能够以科学的态度去认识生命世界,认同人类活动对生物圈的影响,形成环境保护意识,并使这种意识转变成真正的行动,培养学生保护环境的意识,增强爱国主义思想1.认同人类活动对生物圈的影响,形成环境保护意识 2.做到从实际行动出发保护环境1.采取让学生收集资料,整理资料,解疑

语文下册教案找春天
图文对照,读中感悟1.学习第1、2自然段。师:要去野外找春天了,课文中的小朋友现在是怀着什么样的心情呢?(高兴的、急切的、激动的)请你也带着这样的心情读一读第一、二自然段吧?自由读。指名读本段,读后评价悟出应把“脱”、“冲”、“奔”重读才能更加体现出孩子们找春天的迫切心情。2.请大家自由读第3 ~7自然段,想一想,作者把春天想象成什么了(一个害羞的小姑娘)。这个害羞的小姑娘,遮遮掩掩、躲躲藏藏的,不想让人们发现她。可是细心的小朋友还是找到了她。这些小朋友都在哪找到她了?你知道吗?从书中找到有关的句子再读一读。(学生边画、边读。)小草从地下探出头来,那是春天的眉毛吧?早开的野花一朵两朵,那是春天的眼睛吧?树林吐出点点嫩芽,那是春天的音符吧?解冻的小溪丁丁咚咚,那是春天的琴声吧?

部编人教版三年级上册《灰雀》说课稿
一、说教材 《灰雀》是统编教材小学语文三年级上册第八单元的一篇精读课文,这篇课文讲述的是列宁、灰雀和一个孩子之间的故事。列宁在公园里寻找三只惹人喜爱的灰雀当中的一只时,遇到了将灰雀捉走的男孩,经过交谈,受到感动的男孩将灰雀放了回来。这个故事体现了列宁善解人意,对男孩的尊重、爱护以及男孩的诚实和天真。 通过语言和行动来揭示人物的内心世界,展现事件的发展进程,是本篇课文在表达上的主要特点。男孩的语言和行为已经告诉列宁,灰雀的消失与他有关;如何使孩子认识到将灰雀捉走是错误的从而自愿将小鸟放回来,需要循循善诱。列宁没有问孩子是否将灰雀捉走,也未进行任何说教,而是借助一句“多好的灰雀呀,可惜再也飞不回来了”的感叹,使孩子内心受到震动,从而认识和改正自己的错误。在整个事件中,处处可以发现列宁善于观察对方的言语、行动,既不伤害对方的自尊心,又能使对方认识到错误的巧妙的教育方法,同时,也可以体会到列宁对儿童人格的尊重和爱护。 选编这篇课文的意图,一是要学生认识到列宁对儿童的爱护;二是要通过对人物语言和神态的描写体会人物的心理活动。同时,学生还可以受到爱护鸟类等动物的教育。

部编人教版六年级上册《花之歌》说课稿
一、说教材: 《花之歌》是纪伯伦的散文诗集《泪与笑》中的一首,诗人用花的语言来叙述大自然的话语,文中尽显“纪伯伦风格”中的轻柔、凝练、隽秀与清新。诗人通过花语的倾心流露,构建了一幅大自然活生生的图画,图画中有诗意的浪漫,也有现实的真实,如:“我是诸元素之女:冬将我孕育,春使我开放,夏让我成长,秋令我昏昏睡去”写出了花的成长与芬芳。而“我是亲友之间交往的礼品,我是婚礼的冠冕,我是生者赠予死者最后的祭献”就袒露出了花的凋谢命运,都说纪伯伦的诗有着哲理,寓意深邃,从这就可以看出,诗人是用诗意的叙述和思考的敏锐来书写人生的。 二、说教学目标 1.知识目标: (1)理解、积累本课出现的重点词语。 (2)了解纪伯伦和其艺术风格。 (3)了解课文内容,领悟诗中拟人形象的情感内涵。

人教部编版道德与法制三年级下册万里一线牵说课稿
一、依标扣本,说教材《万里一线牵》是部编版《道德与法治》三年级下册第四单元《多样的交通和通信》的第三个主题中的内容。这个主题主要是了解多样便捷的现代通信方式;通过古今通信方式的对比,感受通信发展给人们带来的便利。本课教学通过帮助学生运用已有的生活经验和调查资料相对比,通过对知识的探究发现问题,从而使学生对现代通信方式的发展有初步了解,知道多种多样的现代通信方式,以及通信方式的发展给人们生活带来的便利。二、以人为本,说学情对于现代通信方式,小学生使用的已经很广泛了,但是小学生真正运用现代通信方式解决生活问题的经验不足、缺乏体验,对本知识点的了解很少。因此,依据学生的生活实际和本课的教学目标,我以学生的生活实际为起点,利用课程资源,使教学与学生生活贴得更近,让学生更好的感受现代通信的迅猛发展,以及给生活带来的无限便捷,体验通信愉悦,并在以后的生活中学会合理运用通信方式解决实际问题,更好地服务于当下和未来的生活。
道德与法治七年级下册做情绪情感的主人作业设计
10.阅读材料,回答问题。材料一:近年来,公路上经常出现“路怒族” ,只要看到别人抢道、开车慢、不让道等他们就会 骂人,而且骂得很难听,甚至大打出手。材料二:在新型冠状病毒肺炎疫情防控期间,2020年2月1 日贵州省贵阳市的某商场,一位打扮靓 丽的年轻女子要进入商场时不戴口罩,被商场门口执勤的店员劝阻,要求戴上口罩才能进入商场,该 女子不但不听劝告,而是嗤鼻一笑,不以为然。随后就绕开工作人员打算进入商场,4名工作人员随 后上前阻止,该女子竟然要强行闯入商场,甚至对商场工作人员拳脚相加,随后商场工作人员报警。(1) 结合材料说说,情绪受哪些因素的影响?(2) 根据材料谈谈在生活中如何管理愤怒?11.【东东的日记】下面是东东的“微日记”片段,记录着成长的点滴,与你分享。

道德与法治八年级下册人民当家作主作业设计
①坚持依法行政,维护公平正义②严格遵循诉讼程序,加强立法③司法过程和结果都要合法、公正④坚持以事实为根据,以法律为准绳A.②④ B.②③ C.③④ D.①②3.疫情防控期间,某地检察院充分发挥检察职能,与公安机关等部门加强协作, 提前介入涉疫案件侦查,切实保障人民群众合法权益,全力维护疫情期间社会稳 定。由此可见 ( )①人民检察院是我国的法律监督机关②公安机关是我国的审判机关③公平正义需要法治的保障④人民检察院接受政府的领导和约束A.①② B.①③ C.②③ D.②④(二) 非选择题4. 探究与分享:结合所学知识,与同学讨论探究,回答下列问题。案例反思:2017 年 4 月 20 日,最高人民法院、中央电视台联合公布 2016 年推动法治进程十大案件评选结果,聂某被宣判无罪案等十大案件入选。1995 年 3 月,石家庄中院一审判处聂某死刑,同时判处赔偿受害人家属丧葬费等计 2000 元。1995 年 4 月 27 日,聂某被执行死刑。2016 年 12 月 2 日,最高人民法 院第二巡回法庭宣告撤销原审判决,改判聂某无罪。2017 年 3 月,聂某家属获 268.13991 万元国家赔偿。思考:如何才能避免这种错案的发生?
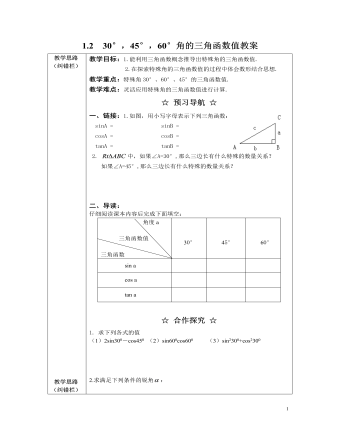
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中七年级数学下册多项式与多项式相乘教案
解:(ax2+bx+1)(3x-2)=3ax3-2ax2+3bx2-2bx+3x-2.∵积不含x2项,也不含x项,∴-2a+3b=0,-2b+3=0,解得b=32,a=94,∴系数a、b的值分别是94,32.方法总结:解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程解答.三、板书设计1.多项式与多项式的乘法法则:多项式和多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.2.多项式与多项式乘法的应用本节知识的综合性较强,要求学生熟练掌握前面所学的单项式与单项式相乘及单项式与多项式相乘的知识,同时为了让学生理解并掌握多项式与多项式相乘的法则,教学中一定要精讲精练,让学生从练习中再次体会法则的内容,为以后的学习奠定基础

北师大初中七年级数学下册单项式除以单项式教案
光的速度约为3×108米/秒,一颗人造地球卫星的速度是8×103米/秒,则光的速度是这颗人造地球卫星速度的多少倍?解析:要求光速是人造地球卫星的速度的倍数,用光速除以人造地球卫星的速度,可转化为单项式相除问题.解:(3×108)÷(8×103)=(3÷8)·(108÷103)=3.75×104.答:光速是这颗人造地球卫星速度的3.75×104倍.方法总结:解整式除法的实际应用题时,应分清何为除式,何为被除式,然后应当单项式除以单项式法则计算.三、板书设计1.单项式除以单项式的运算法则:单项式相除,把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.2.单项式除以单项式的应用在教学过程中,通过生活中的情景导入,引导学生根据单项式乘以单项式的乘法运算推导出其逆运算的规律,在探究的过程中经历数学概念的生成过程,从而加深印象

北师大初中七年级数学下册单项式与单项式相乘教案
解析:先求出长方形的面积,再求出绿化的面积,两者相减即可求出剩下的面积.解:长方形的面积是xym2,绿化的面积是35x×34y=920xy(m2),则剩下的面积是xy-920xy=1120xy(m2).方法总结:掌握长方形的面积公式和单项式乘单项式法则是解题的关键.三、板书设计1.单项式乘以单项式的运算法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里面含有的字母,则连同它的指数作为积的一个因式.2.单项式乘以单项式的应用本课时的重点是让学生理解单项式的乘法法则并能熟练应用.要求学生在乘法的运算律以及幂的运算律的基础上进行探究.教师在课堂上应该处于引导位置,鼓励学生“试一试”,学生通过动手操作,能够更为直接的理解和应用该知识点

北师大初中七年级数学下册等腰三角形的性质教案
方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.三、板书设计1.等腰三角形的性质:等腰三角形是轴对称图形;等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴;等腰三角形的两个底角相等.2.运用等腰三角性质解题的一般思想方法:方程思想、整体思想和转化思想.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中七年级数学下册多项式除以单项式教案
一、情境导入1.计算:(1)-6x3y4z2÷(-23x2y2);(2)9mn÷(-6mn)2·(13n2);(3)6(a-b)3c5÷[-35(a-b)2c]·[-2(a-b)3c4].2.m(a+b+c)=am+bm+cm,(am+bm+cm)÷m=am÷m+bm÷m+cm÷m=a+b+c.你能根据多项式乘以单项式的运算归纳出多项式除以单项式的运算法则吗?二、合作探究探究点:多项式除以单项式【类型一】 直接利用多项式除以单项式进行计算计算:(72x3y4-36x2y3+9xy2)÷(-9xy2).解析:根据多项式除以单项式,先用多项式的每一项分别除以这个单项式,然后再把所得的商相加.解:原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)+9xy2÷(-9xy2)=-8x2y2+4xy-1.方法总结:多项式除以单项式,先把多项式的每一项都分别除以这个单项式,然后再把所得的商相加.

北师大初中七年级数学下册用关系式表示的变量间关系教案
方法总结:观察表中的数据,发现其中的变化规律,然后根据其增减趋势写出自变量与因变量之间的关系式.三、板书设计1.用关系式表示变量间关系2.表格和关系式的区别与联系:表格能直接得到某些具体的对应值,但不能直接反映变量的整体变化情况;用关系式表示变量之间的关系简单明了,便于计算分析,能方便求出自变量为任意一个值时,相对应的因变量的值,但是需计算.本节课的教学内容是变量间关系的另一种表示方法,这种表示方法学生才接触到,学生感觉有点难.这节课的重点是让学生掌握用关系式与表格表示变量间的关系,难点是理解这两种表示方法的优缺点.就此问题,通过让学生对几个例子比较、讨论、总结、归纳两种方法的优点来解决,这样学生就能很好地区分这两种表示方法,并能对不同的问题选择恰当的方法

北师大初中七年级数学下册利用“边边边”判定三角形全等教案
解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n边形的一个顶点可以作(n-3)条对角线,把多边形分成(n-2)个三角形,所以,要使一个n边形木架不变形,至少需要(n-3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.三、板书设计1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”.2.三角形的稳定性本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练



