-

图书馆2023年度工作总结
7.完成图书馆业务数据上报及网站管理工作。每季度按时完成数据上报工作,对微信公众号、APP随时进行更新和管理,本年度APP发布信息65条,政府网45条,直播35条,图书馆网站采用25条,省图书馆订阅号采用12条,确保图书馆业务和宣传工作顺利进行。二、存在的问题虽然今年我馆建设取得不错成效,但依然存在以下问题,一是馆内空间有限,部分硬件设施、办公设备亟待更新。二是馆员数字化、智慧化技能水平有待提高,难以满足图书馆高质量发展需要。三是对外宣传推广力度不够,部分读者对图书馆业务服务和馆藏资源了解不足。三、2024年工作打算新的一年里,我馆将深入贯彻落实《公共图书馆法》《省公共文化服务保障条例》,以第七次全国县级以上公共图书馆评估定级工作为契机,坚持“以评促建、以评促管、以评促效能提升”原则,补短板、强弱项,加快推进标准化图书馆建设,不断推动我县(区)公共图书馆事业高质量持续发展,为建设“书香*”贡献新的更大力量。

2023年度工作总结汇编
第二部分:我们的运营情况我们认为合作公司的优势在于一是有效利用村级资源,比如今年月11份,我们以乡村振兴为契机,利用农闲劳动力,承接乡村振兴项目建设,二是资源融合。合作公司可以整合整个村集体的资源资产,介入土地经营权流转、农村闲置房屋产权等市场交易。三是重点发展红栀子基地、果树种植采摘等项目,利用闲置荒地租赁土地200亩种植苗圃基地,以镇政府为主,主导张家港广水市城南创业工业园,张家港美丽乡村建设.四是抱团发展。我们李店镇目前20个村已经全部成立了人民公司,各有优势特长,未来我们可以相互融合、抱团取暖,实现集团化发展。第三部分:我们的共富路径我们的收益分配是,公司分红收益按6:2:2模式分配,即:60%用于再发展;20%用于全体股民按所持股份比例分红;20%用于村公益事业开支(包括奖励助学、文明评选、尊老扶弱等)。

2023年度工作总结汇编(5篇)
二、重点工作开展情况我们紧盯脱贫人口稳定增收,强化产业和就业帮扶,兜牢防贫基础。一是抓好务工就业。全县共有XX万人脱贫劳动力(含监测对象XX万人)外出务工就业,超省定年度目标XX个百分点。按照每人100元标准兑现发放跨省务工交通补贴XX万元。全县开发公益性岗位XX个,在运营就业帮扶车间53个,共计带动脱贫劳动者XX人就近就业。制定出台《XX县创建乡村振兴“宜业工坊”实施方案》,组织认定第一批“宜业工坊”51家;二是抓好金融帮扶。为有产业发展需求的脱贫户、监测户提供贷款,今年新增贷款XX户XX万元,较去年增加XX%,小额信贷贷款余额达XX亿元,户贷率为35.6%。三是抓好光伏帮扶。压实光伏电站运维管护责任,健全日常管护和市场化运维机制,巩固提升光伏电站帮扶成效,今年累计兑现村级收益XX万元、脱贫户收益XX余万元。

乡2023年三季度工作情况总结
三、下步打算(一)坚持高质量发展,不断增强经济实力坚持把财税工作作为工作重点,积极拓展税源,不断筑牢财政基础。进一步加快项目验收等相关工作。加速推动争资争项指标任务完成。(二)坚持发展现代农业,不断优化产业结构坚持生态高效种养导向,全面落实单产提升晚稻面积2.8万亩。在创建单产提升示范区的大背景下,加速实现农业种植规模化、高效化,打造好河泊潭千亩生态高效农业示范片,以科技赋粮实现水稻增产、农民增收、绿色发展目标。(三)坚持美丽乡村建设,不断改善村容村貌创新制定人居环境领导责任制,包村干部全部深入各村,打桩定位领任务,带头上户做好人居环境劝导、整治等工作。充分发挥示范带动引领,推动荞麦湖村、河泊潭村、磊石村三个乡村振兴示范点建设,以点带面推动全乡人居环境整治提档提质,让绿色成为凤凰最鲜明的底色。

镇2023年度工作总结
三、2024年工作计划一是依托2024年项目库建设谋划项目落实。为进一步巩固拓展脱贫攻坚成果同乡村振兴有效衔接,确保项目提质增项,发挥项目引领带动作用,XX镇经D委会多次认真研讨,紧紧围绕“乡村要发展,产业是关键的”重点,2024年在丹麻、吕湾、斜头、XX、阳洼、岳山6村实施护坡建设项目,共计XXm³,预计投入资金XX万元;在丹麻、高营、岳山3村实施挡土墙建设项目共计XXm³,预计投入资金XX万元;在五方、丹麻、吕湾、斜头、XX、高营、岳山7村实施水渠建设项目共计XX米,预计投入资金XX万元,在XX镇岳山村地质灾害点治理项目XXm³,预计投入资金XX万元;实施太阳能路灯XX盏;以“四个规范”为抓手,全力打造岳山村、樱桃沟村为“有高度、有温度、有热度”的D群服务中心。

乡2024年三季度工作情况总结
一是经济运行仍有短板。发展步伐仍需加快,高质量发展动能不够强劲,经济总量不大;产业结构不够优化,农业大而不强,规模化、产业化、科技化程度较低。二是乡村建设仍有压力。生态环境保护任务还十分繁重,农村垃圾、污水、厕所“三大革命”还需持续加强;乡村基础设施建设需进一步提升,部分村道路交通、农田水利等基础设施亟待提质。三是民生领域仍有欠账。存在主体责任落实不到位、资料台账不规范、收入统计不细致、结对帮扶措施不精准等问题。三、下步打算(一)坚持高质量发展,不断增强经济实力坚持把财税工作作为工作重点,积极拓展税源,不断筑牢财政基础。进一步加快项目验收等相关工作。加速推动争资争项指标任务完成。(二)坚持发展现代农业,不断优化产业结构坚持生态高效种养导向,全面落实单产提升晚稻面积2.8万亩。在创建单产提升示范区的大背景下,加速实现农业种植规模化、高效化,打造好河泊潭千亩生态高效农业示范片,以科技赋粮实现水稻增产、农民增收、绿色发展目标。

教师在年度德育工作总结
沟通协调不够顺畅:在德育工作的实施过程中,我们需要与多个部门进行沟通和协调,但是有时候会出现沟通不畅的情况,影响工作的效果。今后我们将加强沟通协调,确保工作的顺利开展。学生自我管理不够到位:虽然我们开展了班级管理工作,但是有些学生的自我管理还不够到位,容易出现违纪行为。今后我们将加强学生的自我管理,培养他们的自我约束能力。四、工作展望及建议在今后的德育工作中,我们将继续努力,争取取得更好的成绩。具体措施如下:加强德育工作的组织和管理,提高工作的质量和参与度。加强学生的自我管理和自我约束能力,减少违纪行为的发生。加强德育工作的创新和拓展,提高工作的多样性和实效性。总之,本学年的德育工作取得了一定的成绩,但也存在一些问题。我们将继续努力,加强德育工作的组织和管理,提高工作的质量和参与度,为学生提供更好的学习和生活环境。

2024年改革办一季度工作总结
二是试点工作有所突破。今年一季度,全**4个单位共争取国家级和省级改革试点4项。其中,国家级试点2项【市场监管总局选择****作为“个转企”国家级试点**,团中央批准****街道社**为“团中央社**青春行动试点社**”】;省级试点2项【**省民政厅批准社工站打造成省级示范社工站,团省委批准****街道社**打造成全省共青团城市基层组织改革试点】。三是改革氛围日渐浓厚。持续加强对改革的宣传推介和政策解读,不断提高人民群众的知晓度、关注度和满意度。持续加大先进典型和成功经验的宣传力度,积极向市委改革办推介**改革的典型经验和特色亮点。我**行政审批局颁发全省首张“个转企”营业执照的相关新闻在中国经济网、**日报、长城网等央媒和省市媒体刊发,受到了一致好评。

2024年度工作计划汇编(18篇)
1.市政基础设施项目5项,总建设里程2.13km,投资概算2.28亿元。其中,烔炀大道(涉铁)工程施工单位已进场,项目部基本建成,正在办理临时用地、用电及用水等相关工作;中铁佰和佰乐(巢湖)二期10KV外线工程已签订施工合同;黄麓镇健康路、纬四路新建工程均已完成清单初稿编制,亟需黄麓镇完成图审工作和健康路新建工程的前期证件办理;公安学院配套道路项目在黄麓镇完成围墙建设后即可进场施工。2.公益性建设项目6项,总建筑面积15.62万㎡,投资概算10.41亿元。其中,居巢区职业教育中心新建工程、巢湖市世纪新都小学扩建工程已完成施工、监理招标挂网,2月上旬完成全部招标工作;合肥职业技术学院大维修三期已完成招标工作,近期签订施工合同后组织进场施工;半汤疗养院净化和医用气体工程已完成招标工作;半汤疗养院智能化工程因投诉暂时中止;巢湖市中医院(中西医结合医院)新建工程正在按照既定计划推进,预计4月中下旬挂网招标。

2024年一季度D委工作总结及二季度工作打算
二、二季度工作打算坚持把“D的建设”作为国有企业发展的初心,强化高质量发展的引领。(一)持续抓好理论知识学习。严格执行“第一议题”和中心组旁听制度,实现D委理论学习教育化常态化。采取辅导讲座、专家授课、外出观摩、观看专题片等形式,进一步增强学习效果。把学习D的二十大精神作为D员教育培训的重要内容,组织开展“学习二十大精神”主题D日、“我来讲DK”、现场红色教育等活动,提高全体D员干部的政治大局观、科学发展观。(二)持续抓好D建品牌创建。以各基层D支部为主体,坚持“参与性强、重点突出、对象鲜明”的导向,每个支部分别创建1至2个D建品牌,实现由“特色”向“品牌”的升华。(三)持续抓好形势任务教育。持续深入开展“两珍惜、两保持”形势任务教育,编写形势任务教育辅导材料,加强宣教宣讲,引导各级团结一致向前看,凝心聚力谋发展。注重发挥新闻媒体舆论引导作用,在AAA公众号、矿区广播开办形势任务教育专栏,通过创作微电影、短视频、录制广播等形式,扩大形势任务教育效果。

(5篇)本年度第一季度工作总结汇编
二、存在问题(一)文物保护经费未能纳入财政预算。按照相关文物保护法,县级以上人民政府应当将文物保护事业纳入本级国民经济和社会发展规划,所需经费列入本级财政预算。但由于县级财政困难,文物保护经费一直未能纳入财政预算。(二)日常维护措施落实难。县级文物保护机构专业技术人才不足,乡(镇、街道)基本无文物专业技术人员。一些日常维护措施还得不到落实。(三)保护和利用矛盾凸显。由于价值、产权等诸多原因,很多文物未能得到很好地利用,处于闲置或无人使用状态,无人使用或无管理单位的文物在管理中找不到管理相对方,一些安全隐患整改和日常管理等问题很难得到落实,县级文物行政主管部门很难发挥监督管理作用。(四)乡(镇、街道)、村(居)两级对文物保护工作主动性不够。乡(镇、街道)、村(居)两级没有文物保护机构,也没有落实专人负责管理。许多文物保护单位、未核定保护等级的文物缺乏日常维护,处于无人管理状态。
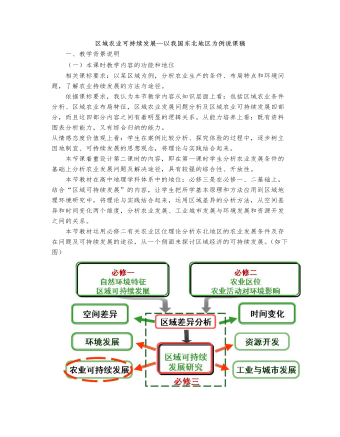
人教版高中地理必修3区域农业可持续发展—以我国东北地区为例说课稿
(3)师生讨论,提升思维深度。教师引领学生将讨论由农业生态破坏、土地利用不合理等表象问题逐步深入到农业结构不合理、农业技术落后等深层问题,提升了学生思维的深度。(4)角色体验,突破难点落实重点。在农民与保护区工作人员的角色体验活动中,学生们尝试换位思考,在冲突与交锋中,在教师的引领下,重新认识环境保护与区域经济发展的关系,在情感体验中加深对可持续发展内涵的理解,小冲突凸显大矛盾是本课设计的创新之处。2.注重对地理问题的探究,突出地理学科本质。地理学科具有综合性、区域性特征,区域差异及人地和谐发展观是我们在教学中应该把握的基本特征,也是我们应当把握的地理学科的本质特征,因此在本节课的设计中我注重抓住地理事物的空间特征、综合性特征,以突出地理学科的本质。

加强离退工作管理制度建设工作情况调研报告
1、传统的工作思路和服务方式亟待转变。 当前我国已经开始进入老龄社会,老干部人员的增加、人员结构以及对服务工作的要求也发生了很大的变化,在新的形势与任务面前,老干部工作如何创新,如何不断开拓工作新思路,如何创新工作方式方法,是我们亟待转变和解决的重要问题之一。 2、离休干部与退休干部的管理服务工作中存在的矛盾亟待解决。 当前离退休干部的整体状况是,离休干部的人员比重越来越小,退休干部的人员比重越来越大,工作压力越来越大,在政策落实上要求向离休干部倾斜,实际工作量上以服务退休干部为主,这是现实工作中普遍存在的问题,做管理型服务还是做劳务型服务,关系到今后的工作导向,这同样是需要认真研究的一个重要问题。

银行员工规章制度学习个人心得通用多篇精选
感触之二:要深刻理解每一条款的内在要求 关于学习员工守则的方式方法,尤其是经过了二级分行举办的“学守则、遵规章”合规知识竞赛的检验,个人认为要学好守则,必须做到一是对守则的条款要理解性记忆,不可死记硬背。能记忆并熟知守则的条款内容是贯彻落实好守则的前提,虽然不能排除极少数人有超人的记忆能力的可能,但绝大多数人的记忆能力都差不多,所以我们在记忆时要充分理解每一个条款,抓住关键字词记忆,如勤勉尽职部分,我们应知道勤勉尽职在守则中体现的就是“制度要求、专业水准、工作效率以及禁止性规定”,坚持专业水准当然要加强学习,不断提高;提高工作效率当然要科学管理时间,不相互扯皮等;二是要联系记忆。即把守则中倡导我们作什么,禁止我们做什么联系起来,找出不同要求间的深层的联系,如关于员工在工作中如何做到依法合规方面,可以提炼出“倡导我们牢固树立法律意识和合规意识,禁止任何以违规为代价的追求利益行为”,这样对整个依法合规部分的记忆就会容易些;

公司管理制度(适用于证券、黄金、外汇投资公司)
一.总经办部门职责1.总经理岗位职责1)负责制定公司年度经营及管理计划,并组织协调、授权各分管副总经理组织实施,确保年度经营指标的全面落实。2)负责组织实施董事会决议及公司年度经营计划和投资方案。3)负责拟定公司内部管理机构方案,组织制定公司规章制度及管理体系,主持管理评审活动。4)负责召集总经理例会,通过各部门的工作报告,监督检查经营管理项目的执行情况及公司财务收支计划的执行结果,提出有效的纠正措施;对经营环节等出现的问题,应及时进行协调、解决,确保年度经营目标的实现。5)负责召集经营管理专题决策会议,依据外部环境的变化趋势和公司内部出现的问题,对经营目标和经营管理提出调整和修订方案。6)负责定期参与董事会会议,对公司年度经营管理计划和执行情况及重大经营管理项目的实施情况作出专题汇报。7)负责制定公司人力资源的管理规定,加强员工队伍建设,负责员工的岗位设置、聘任、调动、考核、奖罚及晋升,维护员工的合法权益。8)负责高层管理人员的培训和指导,并通过逐级负责的原则,全面提高公司员工的整体素质。2.副总经理岗位职责1)协助配合总经理搞好公司的全面工作,执行总经理办公会决议,在重大问题上必须同总经理保持一致。2)协助总经理制定公司年度经营及管理计划,通过年度指标分解,下达到公司各部门组织实施,确保年度经营指标的全面落实。3)按分工协助总经理的日常行政和管理活动,审核公司的组织结构与人员调整方案,定期向总经理报告分管工作。4)负责组织制定分管部门的管理考核标准,协助组织拟定分公司员工管理条例、职场管理制度,加强各个部门执行基本制度的指导和严格管理,确保员工队伍整体素质的提高。5)负责组织签订各部门的目标责任书及市场信息,督导各业务部门做好市场开拓及客户服务工作,规避企业风险,确保营销目标的顺利完成。6)负责部门经理的工作汇报,对各部门经理在一线发现的问题及解决方案进行仔细研究,并及时解决出现的问题和矛盾,提高工作效率。如遇重大事件,应及时向总经理汇报。7)营造良好的工作环境,协调好上下级关系,带领好各部门开展好工作,发扬团队精神。8)完成公司和总经理交办的其它工作任务。

【高教版】中职数学基础模块上册:5.2《弧度制》优秀教案
课 程数学章节内容 课程类型新课课时安排2课时指导教师 日期12月 7 日学习目标掌握用弧度表示角度的大小学习重点掌握用弧度表示角的方法学习难点弧度制和角度制的互换回顾(温故知新)1、回顾上节课所学内容:任意角度的推广、终边相等的角的表示方法; 2、已经学过角度的计量单位:度,度分秒是如何换算的; 3、圆的周长公式和扇形弧长公式。问题(顺着问题找思路)1、弧度制:等于半径长的圆弧所对的圆心角叫做__________,记作____弧度或1________。 2、正角的弧度为_____数,负角的弧度为_____数,零角的弧度为零。 3、由弧度的定义可知,当角α用弧度来表示,其绝对值|α|和圆弧长l与圆的半径r有:|α|=________。 4、一个圆的周长为_____,所以一周角(360°)的弧度为_______=______(rad) 。 5、360°=_____(rad); 180°=_______(rad); 思考如何将角度制转化为弧度制?如何将弧度制转化为角度制?(结合实例讲解)练习(通过练习固要点)1、练习5.2.1; 2、例3;展示(通过展示强能力)(25分钟)(包括学生展示回顾、问题、练习、小组总结等部分)1、引导各小组展示学习成果,在有各小组长指定小组成员展示,结束后,该组组长须总结或指定其他成员进行总结。 2、展示过程中,提醒同学注意老师的板书,或者请老师进行总结,或题目的讲解。

第八周国旗下讲话稿:高度的自制力是成功的基本要素
春天悄然而知,春风轻轻地吹红了鲜花,春雨也静静地润绿了大地,蓬勃的你们正像那红花绿叶一样鲜活,一样有生命力。而在这样一个美丽的季节里,我带给大家的是一句忠告:那就是高度的自制力是成功的基本要素。说热忱是促使你采取行动的重要动力,而自治则是指引你行动方向的平衡轮。有一个故事是这样的:一个商人需要一个伙计,他便在窗户上贴上了一张独特的广告:招聘一个能自我克制的男士,每星期4美元,合适者可以拿6美元。“自我克制”这个术语在村子里引起了议论,自然引起了小伙子们、家长们的思考,同样也引来了众多的求职者。而每个求职者都要经过一个测试。“能阅读吗?”“能,先生”“你能读一读这一段吗?”他把一张报纸放到小伙子的面前“可以,先生”“你能一刻不停的朗读吗?”“可以,先生”“很好,请跟我来”商人把他带到他的私人办公室,然后关上门,他把报纸送到小伙子手中,上面写着他答应一刻不停地读完的那段话,阅读刚开始,商人就放出六只可爱的小狗,小狗跑到男孩的脚边,“这太过分了”男孩经受不住诱惑,要看看美丽的小狗,由于视线离开了阅读的材料,男孩忘记了自己的角色,读错了,当然他也就失去了这个机会。

人教版高中历史必修1从汉至元政治制度的演变教案
【教学方法】本节课的教学知识点比较琐碎,学生学习和理解起来有较大的困难。教师在并结合教材中所引的文献资料给予必要的点拨,并依据教材,并在此基础上拓展教材引用有关材料,扩展学生的思维,用思考题的形式,有机地将教材的重点、难点知识串联起来,注意培养学生史论结合、论从史出的良好的历史学习品质。【导入新课】秦始皇统一中国后,继承了商鞅变法的成果和实践了韩非子的理论,创立了封建专制主义中央集权的政治制度,即皇帝制、中央官制和郡县制,把专制主义的决策方式和中央集权的政治制度有机结合起来。秦始皇首创的专制主义中央集权的政治体制为我国延续两千多年的封建社会选择了政治体制的基本模式。西汉王朝建立后,刘邦承袭了秦始皇所开创的统一的封建专制主义中央集权制。通过综合概述上节课内容,导入新课。

人教版高中历史必修1夏、商、西周的政治制度教案3篇
【大宗与小宗的关系:君臣关系、兄弟关系】4、影响:宗法制保证了贵族在政治上的垄断和特权地位,也有利于统治集团内部的稳定和团结。【合作探究】分封制与宗法制的关系两者互为表里、相辅相成:从根本上说,分封制就是宗法制作用于国家地方政治制度的重要举措和体现。宗法制是分封制的内核和纽带,维护贵族统治集团内部的稳定与团结。宗法制与分封制结合紧密,宗法制是西周政治制度的基础,分封制基于宗法制而产生,与宗法制互为表里。小结:我国早期政治制度(夏商周)发展脉络:起源于夏——初步建立于夏商——完善于西周——瓦解于西周末年到春秋——崩溃于战国★问题解答⊙【学思之窗】从这段记载,你能看出商朝的相权有多大吗?答案提示:相是商朝中央最高官吏,相权很大,包括参定政制、主持政务、辅佐商王等,甚至有时可废立商王。

人教版高中历史必修1从汉至元政治制度的演变说课稿2篇
二、君主专制的演进(即中央政治制度的演变)通过地方政治制度演变的学习,掌握方法以后,以学生归纳整理基本线索为主,教师适当点拨,注意纠错。1. 汉承秦制,又有所变化。教师点拨强调继承与发展两个方面。创设情景:同学们看了电视连续剧《汉武大帝》后,知道汉武帝刘彻在继位之后,就急于对西汉王朝的政治制度进行改革。那么,西汉初期中央政治制度的基本框架是怎样的呢?汉武帝为什么要对它进行改革呢?改革后的西汉中央集权制度又是怎样的呢?请大家议一议,想一想。主干知识:西汉初期的中央政治制度的最大特点是“汉承秦制”。具体表现在两个方面:一是继续实行皇帝制度,维护皇权,这一做法也为后来各王朝所沿用;二是在中央设立三公,分别掌管行政、监察和军事。到汉武帝时,“中朝”成为西汉重要的中央决策机构,尚书令的权力日益重要,以丞相为首的三公九卿的权力被削弱,演化为执行机构。到了东汉光武帝时,进一步剥夺三公权限,扩大尚书的权力。





















