-

2021年上海中考语文试题及答案
年轻时,朱伯是研究所里做什么都要精益求精的工程师。 后来,他开了间“玩具诊所”,专门修补上了年头的玩具:毛绒娃娃、火车侠、奥特曼……成为玩具修复师以来,朱伯早上8点起床,有时忙到晚上12点,至今已修复了数千个玩具。他喜欢叫玩具患者为“小朋友”,每个“小朋友”都有一个故事。

2020年上海中考语文试题及答案
支教的最后一天,为了给我送行,孩子们早早来到学校画黑板画、贴气球、布置教室。他们的欢笑声像高原洁净的空气一般清新怡人,节目是孩子们提前好几天排练的,每表演完一个,我都拼命鼓掌。

2013年上海中考语文试题及答案
老妈每天都要问我一个问题:“百合有电话吗?”百合是我女儿,在北京念大二。老妈耳朵背,我附耳回答:“有电话。”过不了多久,老妈又问:“百合有电话吗?”

2012年上海中考语文试卷及答案
要审视自己。我们往往容易看到别人的缺点,却不容易看到自己的不足。“为什么看见你弟兄眼中的刺,却不想自己眼中有梁木呢?”说的就是这个道理。如果我们面对别人的过错,能够严格审视自己,就可以更加理性地看待问题。

2016年上海中考语文试题及答案
乐乐:欢欢,我发现这里的马路名是我国的某些省份名或城市名,比如南京路、北京路、西藏路、福建路,还有以我的故乡四川命名的呢!欢欢:(2)乐乐:我还想请教你,你的学校在静安区,这名字有来由吗?

2015年上海中考语文试题及答案
那年我上小学三年级。寒假前到学校拿学期成绩单。回家时我和六七个没带书包的好友同行。刚领的成绩单拿在手上,已经被我们折得皱巴巴了。

2014年上海中考语文试题及答案
爱因斯坦与上海有特殊的情缘,他曾在1922年两次到访上海,前一次他踏上堤岸就获悉自己得到诺贝尔物理奖的消息;后一次他在福州路工部局礼堂演讲“相对论”,这两次抵沪,他都入住在理查饭店,即今天外滩的浦江饭店。

2009年上海中考语文试题及答案
他告诉我,他是一名高中生,但对学习没有一点兴趣,他的爱好是摄影。他每天都沉迷于摄影当中,学习成绩非常差。父母对他的“不务正业”极为不满,经常指责他。就在两个月前,他最心爱的老相机被愤怒的父亲摔碎了,他一气之下离家出走,和一群网上认识的志愿者来到了这里——梦想了好久的目的地。

2008年上海中考语文试题及答案
小镇只有一所大学,不大,但哪个国家的学生都有。中国来的一共五名,巧了,全是女生,名付其实五朵金花。珍妮是她们的头儿。五朵金花同吃住同进出,像一家子出来的。其实本来就是一家子。

2010年上海中考语文试题及答案
那一年,我即将大学毕业,为了找个单位,天天出去“扫街”,但仍一无所获。我学的是建筑设计专业,找了几家建筑设计院,人家要的不是博士就是硕士。一负责人看着我的简历说,你读书时,还获过不少奖,不错!可是,我们这里暂时不缺建筑设计方面的人才,要不你先来我们这里干个保安什么的吧!等有机会再安排你。

人教版高中数学选修3排列与排列数教学设计
4.有8种不同的菜种,任选4种种在不同土质的4块地里,有 种不同的种法. 解析:将4块不同土质的地看作4个不同的位置,从8种不同的菜种中任选4种种在4块不同土质的地里,则本题即为从8个不同元素中任选4个元素的排列问题,所以不同的种法共有A_8^4 =8×7×6×5=1 680(种).答案:1 6805.用1、2、3、4、5、6、7这7个数字组成没有重复数字的四位数.(1)这些四位数中偶数有多少个?能被5整除的有多少个?(2)这些四位数中大于6 500的有多少个?解:(1)偶数的个位数只能是2、4、6,有A_3^1种排法,其他位上有A_6^3种排法,由分步乘法计数原理,知共有四位偶数A_3^1·A_6^3=360(个);能被5整除的数个位必须是5,故有A_6^3=120(个).(2)最高位上是7时大于6 500,有A_6^3种,最高位上是6时,百位上只能是7或5,故有2×A_5^2种.由分类加法计数原理知,这些四位数中大于6 500的共有A_6^3+2×A_5^2=160(个).

人教版高中数学选修3超几何分布教学设计
探究新知问题1:已知100件产品中有8件次品,现从中采用有放回方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.(1):采用有放回抽样,随机变量X服从二项分布吗?采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即X~B(4,0.08).(2):如果采用不放回抽样,抽取的4件产品中次品数X服从二项分布吗?若不服从,那么X的分布列是什么?不服从,根据古典概型求X的分布列.解:从100件产品中任取4件有 C_100^4 种不同的取法,从100件产品中任取4件,次品数X可能取0,1,2,3,4.恰有k件次品的取法有C_8^k C_92^(4-k)种.一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为P(X=k)=CkM Cn-kN-M CnN ,k=m,m+1,m+2,…,r.其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M},则称随机变量X服从超几何分布.

人教版高中数学选修3全概率公式教学设计
2.某小组有20名射手,其中1,2,3,4级射手分别为2,6,9,3名.又若选1,2,3,4级射手参加比赛,则在比赛中射中目标的概率分别为0.85,0.64,0.45,0.32,今随机选一人参加比赛,则该小组比赛中射中目标的概率为________. 【解析】设B表示“该小组比赛中射中目标”,Ai(i=1,2,3,4)表示“选i级射手参加比赛”,则P(B)= P(Ai)P(B|Ai)= 2/20×0.85+ 6/20 ×0.64+ 9/20×0.45+ 3/20×0.32=0.527 5.答案:0.527 53.两批相同的产品各有12件和10件,每批产品中各有1件废品,现在先从第1批产品中任取1件放入第2批中,然后从第2批中任取1件,则取到废品的概率为________. 【解析】设A表示“取到废品”,B表示“从第1批中取到废品”,有P(B)= 112,P(A|B)= 2/11 ,P(A| )= 1/11所以P(A)=P(B)P(A|B)+P( )P(A| )4.有一批同一型号的产品,已知其中由一厂生产的占 30%, 二厂生产的占 50% , 三厂生产的占 20%, 又知这三个厂的产品次品率分别为2% , 1%, 1%,问从这批产品中任取一件是次品的概率是多少?

人教版高中数学选修3条件概率教学设计
(2)方法一:第一次取到一件不合格品,还剩下99件产品,其中有4件不合格品,95件合格品,于是第二次又取到不合格品的概率为4/99,由于这是一个条件概率,所以P(B|A)=4/99.方法二:根据条件概率的定义,先求出事件A,B同时发生的概率P(AB)=(C_5^2)/(C_100^2 )=1/495,所以P(B|A)=(P"(" AB")" )/(P"(" A")" )=(1/495)/(5/100)=4/99.6.在某次考试中,要从20道题中随机地抽出6道题,若考生至少答对其中的4道题即可通过;若至少答对其中5道题就获得优秀.已知某考生能答对其中10道题,并且知道他在这次考试中已经通过,求他获得优秀成绩的概率.解:设事件A为“该考生6道题全答对”,事件B为“该考生答对了其中5道题而另一道答错”,事件C为“该考生答对了其中4道题而另2道题答错”,事件D为“该考生在这次考试中通过”,事件E为“该考生在这次考试中获得优秀”,则A,B,C两两互斥,且D=A∪B∪C,E=A∪B,由古典概型的概率公式及加法公式可知P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)=(C_10^6)/(C_20^6 )+(C_10^5 C_10^1)/(C_20^6 )+(C_10^4 C_10^2)/(C_20^6 )=(12" " 180)/(C_20^6 ),P(E|D)=P(A∪B|D)=P(A|D)+P(B|D)=(P"(" A")" )/(P"(" D")" )+(P"(" B")" )/(P"(" D")" )=(210/(C_20^6 ))/((12" " 180)/(C_20^6 ))+((2" " 520)/(C_20^6 ))/((12" " 180)/(C_20^6 ))=13/58,即所求概率为13/58.

人教版高中数学选修3正态分布教学设计
3.某县农民月均收入服从N(500,202)的正态分布,则此县农民月均收入在500元到520元间人数的百分比约为 . 解析:因为月收入服从正态分布N(500,202),所以μ=500,σ=20,μ-σ=480,μ+σ=520.所以月均收入在[480,520]范围内的概率为0.683.由图像的对称性可知,此县农民月均收入在500到520元间人数的百分比约为34.15%.答案:34.15%4.某种零件的尺寸ξ(单位:cm)服从正态分布N(3,12),则不属于区间[1,5]这个尺寸范围的零件数约占总数的 . 解析:零件尺寸属于区间[μ-2σ,μ+2σ],即零件尺寸在[1,5]内取值的概率约为95.4%,故零件尺寸不属于区间[1,5]内的概率为1-95.4%=4.6%.答案:4.6%5. 设在一次数学考试中,某班学生的分数X~N(110,202),且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分及90分以上)的人数和130分以上的人数.解:μ=110,σ=20,P(X≥90)=P(X-110≥-20)=P(X-μ≥-σ),∵P(X-μσ)≈2P(X-μ130)=P(X-110>20)=P(X-μ>σ),∴P(X-μσ)≈0.683+2P(X-μ>σ)=1,∴P(X-μ>σ)=0.158 5,即P(X>130)=0.158 5.∴54×0.158 5≈9(人),即130分以上的人数约为9人.

人教版高中数学选修3组合与组合数教学设计
解析:因为减法和除法运算中交换两个数的位置对计算结果有影响,所以属于组合的有2个.答案:B2.若A_n^2=3C_(n"-" 1)^2,则n的值为( )A.4 B.5 C.6 D.7 解析:因为A_n^2=3C_(n"-" 1)^2,所以n(n-1)=(3"(" n"-" 1")(" n"-" 2")" )/2,解得n=6.故选C.答案:C 3.若集合A={a1,a2,a3,a4,a5},则集合A的子集中含有4个元素的子集共有 个. 解析:满足要求的子集中含有4个元素,由集合中元素的无序性,知其子集个数为C_5^4=5.答案:54.平面内有12个点,其中有4个点共线,此外再无任何3点共线,以这些点为顶点,可得多少个不同的三角形?解:(方法一)我们把从共线的4个点中取点的多少作为分类的标准:第1类,共线的4个点中有2个点作为三角形的顶点,共有C_4^2·C_8^1=48(个)不同的三角形;第2类,共线的4个点中有1个点作为三角形的顶点,共有C_4^1·C_8^2=112(个)不同的三角形;第3类,共线的4个点中没有点作为三角形的顶点,共有C_8^3=56(个)不同的三角形.由分类加法计数原理,不同的三角形共有48+112+56=216(个).(方法二 间接法)C_12^3-C_4^3=220-4=216(个).

(中秋节)国旗下讲话:中秋,怀一颗感恩的心
踏着秋天的鼓点,我们走进金色的九月;再过两天我们又将迎来一年一度的中秋佳节,是我国的传统佳节,农历八月十五恰在秋季的中间,故称之中秋节,是仅次于春节的第二大传统节日。每到这一天,许多远离家乡的游子,纷纷赶回家中,与父母亲友欢聚一堂,把酒言欢。中秋的月最圆,最明,最美;中秋月如水如镜,诗情画意,充满浓浓的亲情,又被认为是我们中国人的团圆节。“中秋”一词最早在周朝就已出现,而中秋节的盛行开始于宋朝。 中秋节原是丰收的节日。过去,人们在丰收的季节里,总要大事庆祝一番,庆祝一年的好收成,享受丰收的喜悦。中秋时节云稀雾少,月光皎洁,民间除了要举行赏月、祭月、吃月饼祝福团圆等一系列活动,有些地方还有舞草龙,砌宝塔等活动。中秋节还有许多美好的传说,嫦娥奔月、吴刚折桂、玉兔捣药等等,这些无不寄托着人们对生活无限的热爱和对美好未来的向往。
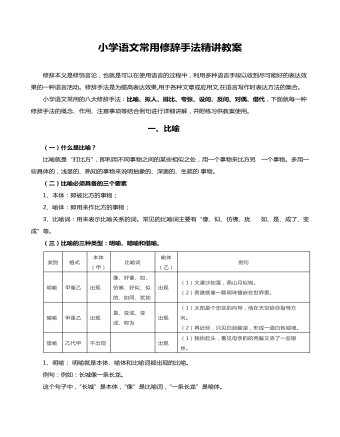
小学语文修辞手法教案专题课件
1、明喻: 明喻就是本体、喻体和比喻词都出现的比喻。例句:例如:长城像一条长龙。这个句子中,“长城”是本体,“像”是比喻词,“一条长龙”是喻体。2、暗喻: 暗喻又叫隐喻,只出现本体和喻体,不用比喻词语或用“是、变成、成为、等于”等喻词。例句:例如:山间的云雾构成了一幅精妙的山水画。这个句子中“山间的云雾”是本体,“构成”是比喻词,“一幅精妙的山水画”是喻体。3、借喻: 借喻是只出现用来代替本体的喻体,而本体和喻词都不出现。例句:落光了叶子的柳树上挂满了毛茸茸、亮晶晶的银条儿。这个句子中,本体、比喻词均没有出现,喻体是“银条儿”。

四川省巴中市2017年中考语文真题试题(含答案)
江城子?密州出猎苏轼老夫聊发少年狂, 左牵黄, 右擎苍, 锦帽貂裘, 千骑卷平冈。 为报倾城随太守, 亲射虎, 看孙郎。酒酣胸胆尚开张。 鬓微霜, 又何妨! 持节云中, 何日遣冯唐? 会挽雕弓如满月, 西北望, 射天狼。

四川省巴中市2017年中考语文真题试题(含解析)
江城子?密州出猎苏轼老夫聊发少年狂, 左牵黄, 右擎苍, 锦帽貂裘, 千骑卷平冈。 为报倾城随太守, 亲射虎, 看孙郎。酒酣胸胆尚开张。 鬓微霜, 又何妨! 持节云中, 何日遣冯唐? 会挽雕弓如满月, 西北望, 射天狼。(1)这首词的词牌名是 ,从本词的题材及语言风格看,是一首 词。(2)词的下片中用遣冯唐的典故表达了什么意思?

