-

直线的两点式方程教学设计人教A版高中数学选择性必修第一册
解析:①过原点时,直线方程为y=-34x.②直线不过原点时,可设其方程为xa+ya=1,∴4a+-3a=1,∴a=1.∴直线方程为x+y-1=0.所以这样的直线有2条,选B.答案:B4.若点P(3,m)在过点A(2,-1),B(-3,4)的直线上,则m= . 解析:由两点式方程得,过A,B两点的直线方程为(y"-(-" 1")" )/(4"-(-" 1")" )=(x"-" 2)/("-" 3"-" 2),即x+y-1=0.又点P(3,m)在直线AB上,所以3+m-1=0,得m=-2.答案:-2 5.直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 . 解析:直线在两坐标轴上的截距分别为1/a 与 1/b,所以直线与坐标轴围成的三角形面积为1/(2"|" ab"|" ).答案:1/(2"|" ab"|" )6.已知三角形的三个顶点A(0,4),B(-2,6),C(-8,0).(1)求三角形三边所在直线的方程;(2)求AC边上的垂直平分线的方程.解析(1)直线AB的方程为y-46-4=x-0-2-0,整理得x+y-4=0;直线BC的方程为y-06-0=x+8-2+8,整理得x-y+8=0;由截距式可知,直线AC的方程为x-8+y4=1,整理得x-2y+8=0.(2)线段AC的中点为D(-4,2),直线AC的斜率为12,则AC边上的垂直平分线的斜率为-2,所以AC边的垂直平分线的方程为y-2=-2(x+4),整理得2x+y+6=0.

直线的一般式方程教学设计人教A版高中数学选择性必修第一册
解析:当a0时,直线ax-by=1在x轴上的截距1/a0,在y轴上的截距-1/a>0.只有B满足.故选B.答案:B 3.过点(1,0)且与直线x-2y-2=0平行的直线方程是( ) A.x-2y-1=0 B.x-2y+1=0C.2x+y=2=0 D.x+2y-1=0答案A 解析:设所求直线方程为x-2y+c=0,把点(1,0)代入可求得c=-1.所以所求直线方程为x-2y-1=0.故选A.4.已知两条直线y=ax-2和3x-(a+2)y+1=0互相平行,则a=________.答案:1或-3 解析:依题意得:a(a+2)=3×1,解得a=1或a=-3.5.若方程(m2-3m+2)x+(m-2)y-2m+5=0表示直线.(1)求实数m的范围;(2)若该直线的斜率k=1,求实数m的值.解析: (1)由m2-3m+2=0,m-2=0,解得m=2,若方程表示直线,则m2-3m+2与m-2不能同时为0,故m≠2.(2)由-?m2-3m+2?m-2=1,解得m=0.

国旗下的讲话-胸前的时尚-领导讲话 - 国旗下讲话
在经济飞速发展的今天,人们越来越热衷于时尚.提到法国巴黎,我们会不由自主地把它和时尚,流行联系在一起.也正是在这个城市,中国人民向全世界展示了独属于中华民族的时尚.在一场模特比赛中,中国模特向时尚的巴黎人民展示了以红色为主色调的 中国传统服饰.这种极具中国传统特色的红色被巴黎人民称作"中国红".一时间,"中国红"在巴黎成了一种时尚色,大街小巷随处可见,就连举世闻名的法国标志性建筑——埃菲尔铁塔也不甘示弱,在展览期间首次披上了红装.每当夜色降临,铁塔上便亮起盏盏红灯,无比壮丽.

法制宣传日国旗下讲话稿:做一个遵纪守法的实中人
同学们、老师们,大家早上好!世上本没有路,走的人多了,也便成了路;世上本没有交通规则,路上的车辆多了,也便出台了交通规则。从人的本性上来说,没有人喜欢被规则约束,人们更多的是对自由的渴望,对无拘无束的生活的向往;但是,没有规则约束的自由不是真正的自由,而是灾难。黄河因为有了堤岸的约束,才能展现它一泻千里、波澜壮阔的奔腾气势,成为哺育中华民族的母亲河,如果没有堤岸或堤岸决口,则会带来致命的洪灾。现代交通,有了合理的交通规则,且能严格遵守的话,才有高速行驶的畅快,才能给人类带来巨大的便利,反之,将引发巨大的灾难。所以,堤岸是河流的保护神,交通规则是驾驶员的保护神,校纪校规是学生的保护神,法律法规是我们所有社会人的共同的保护神。

法制宣传日国旗下讲话稿:严以律已,做遵纪守法的好学生
尊敬的老师、亲爱的同学们:大家早上好!我叫xx,是xx边防派出所的所长,也是一中法制副校长。今天,很高兴又在国旗下为大家上法制课,11月17日和大家一起经历了霞中110周年校庆,一起受到淋浴和熏陶,感受到百年老校散发出的时代活力。今天,非常荣幸和老师、同学们一起探讨一下法律和安全的有关问题。大家知道,12月4日是我国的法制宣传日,本周是法制宣传周。今天我讲话的题目是《严以律已,做遵纪守法的好学生》,内容主要有两个方面,一是坚决摒弃不良习惯,做遵规守法的好学生;二是从我做起,自觉养成良好校园交通习惯。一、坚决摈弃不良习惯,做遵规守法学生。首先,大家要学法知法懂法。俗话说:“没有规矩不成方圆”,自古家有家规,校有校纪,国有国法。只有学习法律知识,才能知道什么是合法,什么是违法,才能分辩是非,识别善恶;只有学法,才能树立民主法制观念,明确公民的权利与义务,才能依法办事,依法维护自身权益。调查表明:中学生中认为法律与我们的生活密切相关的不到一成;认为遇到不法伤害、被敲诈几块钱是小事不必计较的近半。这不能不给我们深刻警示。当学生被敲诈、殴打,他们本应理直气壮地用法律手段保护自己的合法权益,伸张正义,可是,他们都不懂得法律知识,或忍气吞声,或采取极端措施报复,有时糊里糊涂走上犯罪道路。

“国际六一儿童节”国旗下讲话稿:让我们的童年像花儿一样
今天也是我的儿子过的最后一个六一儿童节,暑假以后他就要读七年级了,昨天晚上,儿子和我进行了一番交流:“爸爸,明天你送什么礼物给我啊?”现在生活质量提高了,我们衣食无忧,送给儿子什么礼物呢?我一直在考量这个问题。我认为应该送给他三件礼物。第一件礼物:要有一颗有责任感能担当的心。我们的社会稳定,人民生活安康,这是先辈们用鲜血换来的,没有先辈们的血染沙场何来今日的璀璨辉煌?我们红领巾是先辈们用鲜血染红的,佩戴红领巾是一种信仰,是对先辈们无限地崇敬,是对美好生活的无限追求。我们应该牢记先辈的嘱托,认真学习,刻苦钻研,开拓创新,勇于担当,从我做起,为伟大的“中国梦”描摹上精彩的一笔,树立为实现中国梦而读书的理想。

第六周国旗下讲话稿:敬畏规则,做一名守规则的好少年
有这么一则故事:一个哈佛大学学生,在学校图书馆偷拿了一本珍贵的资料书。不久,一场大火烧毁了图书馆,他偷的书就成了唯一珍品。要不要把书送回去?他犹豫了,不送受到心灵的谴责,送了则有可能被学校开除。经过斗争,他还是决定把书交送给校长。校长先表扬了他敢于认错的精神,然后宣布开除这名学生。很多人觉得校长不讲人情,可是校长的治校理念非常清晰:规则大于人情,让规则看守哈佛更可靠!俗话说:“没有规矩,不成方圆。”那么什么是规则呢?规则就是规定出来让大家遵守的做事规程和行动准则。他告诉我们什么事情可以做,什么事情不可以做。那么,我们在校园中有些什么规则呢?在校园内,我们有一些言行规则:爱护公物,见到老师和同学要主动问好;见到校园路上的垃圾要随手捡起来;不欺负小同学,不和同学说脏话。在课堂上,用心听课,积极思考,举手发言,认真完成作业,都是我们应该遵循的学习规则。

XX年春季第二周国旗下讲话稿:让文明的校园更文明
老师,同学们:早上好!记得有人说过:“人,一撇一捺,写起来容易做起来难。”该做怎样的人呢,一百个人会有一百种答案,但在每一个答案的背后都有一个基点,那就是做人首先要做一个文明的人。本周,我校将迎接泉州市“文明学校”县级考评,今天我国旗下讲话的题目是“让文明的校园更文明”。有这么两则报道,一则说的是新加坡。新加坡是一个通用英语的发达国家,虽然有一部分人使用中文,但是这个国家的公共场所的各种标语都是用英语书写的。但其中的一些文明礼貌的标语,如“不准随地吐痰”、“禁止吸烟”、“不准进入草坪”等却用中文书写,为什么呢?曾经有一位大使问过新加坡当局,得到的回应是:“因为有这些不文明行为的,大多数是中国大陆的游客。”为此,到新加坡考察的一位中学校长语重心长地说:“不文明行为就是国耻。”另一则是中央电视台曾经报道过。某年国庆节后的天安门广场,随处可见口香糖残迹,40万平方米的天安门广场上竟有60万块口香糖残渣,有的地方不到一平方米的地面上,竟有9块口香糖污迹,密密麻麻的斑痕与天安门广场的神圣和庄严形成了强烈反差。

XX年高考倒计时国旗下讲话稿:胸怀梦想,做更好的自己
亲爱的老师们、同学们:上午好!我是来自高三(5)班的周xx,今天我发言的主题是“胸怀梦想,做更好的自己”。今天是XX年的3月27日,距离高考还有72天,三年前我怀揣着梦想与希望走进金沙,一千多个日夜,我时刻记住自己的理想,做更好的自己。汪国真曾说过:“凡是到达了的地方,都是属于昨天,哪怕那山再青,那水再秀,那风再温柔。太深的流连便成了一种羁绊,绊住的不仅是双脚,还有未来。”诗人看似谈的是进退间的从容,我却认为,它实际上囊括了对生命的解读:无论经历几多浮沉,万不要让繁花落寞埋没了你,你得清楚心里究竟想要什么。心中有光,才能一路坚定不移,执着向前。我们金沙人即使如此,只有胸怀梦想,才能奔向远方,做更好的自己。在这里,我想问问所有一起奋战的高三同学们:“你们还记得初进高中时的梦想吗?”高三的一模考试刚结束不久,和其它的考试一样,在成绩公布的那一刻,自然又是几家欢喜几家愁。许多同学在收到成绩单是,似是一下子跌入了低谷,未来只剩下迷茫和不确定性。毕竟一模考试的重要性对每一个高三学生来说都是不言而喻的。到了这个时候,每个人的能力基本上都已经到了一个极限,想要经一部是跟艰难的。然而想倒退一步也许只需要片刻的松懈。

北师大初中数学九年级上册复杂图形的三视图2教案
教学目标:1.会画直棱柱(仅限于直三棱柱和直四棱柱)的三种视图,体会这几种几何体与其视图之间的相互转化。2. 会根据三视图描述原几何体。教学重点:掌握直棱柱的三视图的画法。能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法一、实物观察、空间想像观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过 想像,再抽象出这两个直棱柱的主视图,左视图和俯视图。绘制:请你将抽象出来的三种视图画出来,并与同伴交流。比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法。拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试。

北师大初中数学九年级上册一元二次方程的解及其估算2教案
探索1:上节我们列出了与地毯的花边宽度有关的方程。地毯花边的宽x(m),满足方程 (8―2x)(5―2x)=18也就是:2x2―13x+11=0你能估算出地毯花边的宽度x吗?(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业

北师大初中数学九年级上册正方形的性质1教案
在Rt△ABC中,AC=AB2+BC2=12+12=2(cm),∴FC=AC-AF=2-1(cm),∴BE=2-1(cm).方法总结:正方形被对角线分成4个等腰直角三角形,因此在正方形中解决问题时常用到等腰三角形的性质与直角三角形的性质.【类型三】 利用正方形的性质证明线段相等如图,已知过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.解析:由PE⊥BC,PF⊥CD知四边形PECF为矩形,故有EF=PC,这时只需说明AP=CP,由正方形对角线互相垂直平分可知AP=CP.证明:连接AC,PC,如图.∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.方法总结:(1)在正方形中,常利用对角线互相垂直平分证明线段相等;(2)无论是正方形还是矩形,经常连接对角线,这样可以使分散的条件集中.

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。

北师大初中七年级数学上册比较线段的长短教案1
1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.(1)求线段MN的长;(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出MN的长度吗?请用简洁的话表达你发现的规律.

北师大初中七年级数学上册比较线段的长短教案2
教学反思: 1.本课时设计的主导思想是:将数形结合的思想渗透给学生,使学生对数与形有一个初步的认识.为将来的学习打下基础,这节课是一堂起始课,它为学生的思维开拓了一个新的天地.在传统的教学安排中,这节课的地位没有提到一定的高度,只是交给学生比较线段的方法,没有从数形结合的高度去认识.实际上这节课大有可讲,可以挖掘出较深的内容.在教知识的同时,交给学生一种很重要的数学思想.这一点不容忽视,在日常的教学中要时时注意.2.学生在小学时只会用圆规画圆,不会用圆规去度量线段的大小以及截取线段,通过这节课,学生对圆规的用法有一个新的认识.3.在课堂练习中安排了度量一些三角形的边的长度,目的是想通过度量使学生对“两点之间线段最短”这一结论有一个感性的认识,并为下面的教学做一个铺垫.

北师大初中七年级数学上册从三个方向看物体的形状教案1
1.经历从不同方向观察物体的活动过程,发展空间观念.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的形状.3.能识别从三个方向看到的简单物体的形状,会画立方体及简单组合体从三个方向看到的形状,并能根据看到的形状描述基本几何体或实物原型.一、情境导入观察图中不同方向拍摄的庐山美景.你能从苏东坡《题西林壁》诗句:“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”体验出其中的意境吗?你能挖掘出其中蕴含的数学道理吗?让我们一起探索新知吧!二、合作探究探究点一:从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的,从上面看到的平面图形是()解析:这个几何体从上面看,共有2行,第一行能看到3个小正方形,第二行能看到2个小正方形.故选D.
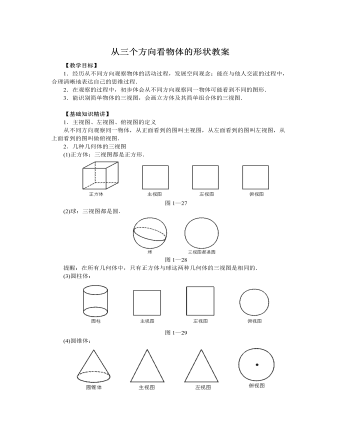
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中七年级数学上册代数式的求值教案1
(1)请你用代数式表示水渠的横断面面积;(2)计算当a=3,b=1时,水渠的横断面面积.解析:(1)根据梯形面积=12(上底+下底)×高,即可用含有a、b的代数式表示水渠横断面面积;(2)把a=3、b=1带入到(1)中求出的代数式中,其结果即为水渠的横断面面积.解:(1)∵梯形面积=12(上底+下底)×高,∴水渠的横断面面积为:12(a+b)b(m2);(2)当a=3,b=1时水渠的横断面面积为12(3+1)×1=2(m2).方法总结:解答本题时需搞清下列几个问题:(1)题目中给出的是什么图形?(2)这种图形的面积公式是什么?(3)根据公式求图形的面积需要知道哪几个量?(4)这些量是否已知或能求出?搞清楚了这些问题,求解就水到渠成.三、板书设计教学过程中,应通过活动使学生感知代数式运算在判断和推理上的意义,增强学生学习数学的兴趣,培养学生积极的情感和态度,为进一步学习奠定坚实的基础.

北师大初中七年级数学上册代数式的求值教案2
解 由题意可得,今年的年产值为a·(1+10%) 亿元,于是明年的年产值为a·(1+10%)·(1+10%)= 1.21a(亿元).若去年的年产值为2亿元,则明年的年产值为1.21a =1.21×2 = 2.42(亿元).答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以预计明年的年产值是2.42亿元.例3 当x=-3时,多项式mx3+nx-81的值是10,当x = 3时,求该代数式的值.解 当x=-3时,多项式mx3+nx-81=-27m-3n-81, 此时-27m-3n-81=10, 所以27m+3n=-91.则当x=3,mx3+nx-81 =( 27m+3n )-81=-91-81=-172.注:本题采用了一种重要的数学思想——“整体思想”.即是考虑问题时不是着眼于他的局部特征,而是把注意力和着眼点放在问题的整体结构上,把一些彼此独立,但实质上又相互紧密联系着的量作为整体来处理的思想方法.

北师大初中七年级数学上册等式的基本性质教案1
方法总结:对等式进行变形,必须在等式的两边同时进行,即同加或同减,同乘或同除,不能漏掉一边,且同加或同减,同乘或同除的数必须相同.探究点二:利用等式的基本性质解方程用等式的性质解下列方程:(1)4x+7=3; (2)12x-13x=4.解析:(1)在等式的两边都减7,再在等式的两边都除以4,可得答案;(2)在等式的两边都乘以6,再合并同类项,可得答案.解:(1)方程两边都减7,得4x=-4.方程两边都除以4,得x=-1;(2)方程两边都乘以6,得3x-2x=24,x=24.方法总结:解方程时,一般先将方程变形为ax=b的形式,然后再变形为x=c的形式.三、板书设计教学过程中,强调学生自主探索和合作交流,通过观察、操作、归纳等数学活动,感受数学思想的条理性和数学结论的严密性.

