-

北师大初中八年级数学下册一元一次不等式组的解法教案
把解集在数轴上表示出来,并将解集中的整数解写出来.解析:分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集,再找出解集范围内的整数即可.解:x+23<1 ①,2(1-x)≤5 ②,由①得x<1,由②得x≥-32,∴不等式组的解集为-32≤x<1.则不等式组的整数解为-1,0.方法总结:此题主要考查了一元一次不等式组的解法,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.三、板书设计一元一次不等式组概念解法不等式组的解集利用数轴确定解集利用口诀确定解集解一元一次不等式组是建立在解一元一次不等式的基础之上.解不等式组时,先解每一个不等式,再确定各个不等式组的解集的公共部分.

北师大初中八年级数学下册直接提公因式因式分解教案
解析:(1)首先提取公因式13,进而求出即可;(2)首先提取公因式20.15,进而求出即可.解:(1)39×37-13×91=3×13×37-13×91=13×(3×37-91)=13×20=260;(2)29×20.15+72×20.15+13×20.15-20.15×14=20.15×(29+72+13-14)=2015.方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.三、板书设计1.公因式多项式各项都含有的相同因式叫这个多项式各项的公因式.2.提公因式法如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种因式分解的方法叫做提公因式法.本节中要给学生留出自主学习的空间,然后引入稍有层次的例题,让学生进一步感受因式分解与整式的乘法是逆过程,从而可用整式的乘法检查错误.本节课在对例题的探究上,提倡引导学生合作交流,使学生发挥群体的力量,以此提高教学效果.

北师大初中八年级数学下册三角形的全等和等腰三角形的性质教案
证明:过点A作AF∥DE,交BC于点F.∵AE=AD,∴∠E=∠ADE.∵AF∥DE,∴∠E=∠BAF,∠FAC=∠ADE.∴∠BAF=∠FAC.又∵AB=AC,∴AF⊥BC.∵AF∥DE,∴DE⊥BC.方法总结:利用等腰三角形“三线合一”得出结论时,先必须已知一个条件,这个条件可以是等腰三角形底边上的高,可以是底边上的中线,也可以是顶角的平分线.解题时,一般要用到其中的两条线互相重合.三、板书设计1.全等三角形的判定和性质2.等腰三角形的性质:等边对等角3.三线合一:在等腰三角形的底边上的高、中线、顶角的平分线中,只要知道其中一个条件,就能得出另外的两个结论.本节课由于采用了动手操作以及讨论交流等教学方法,有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中八年级数学下册异分母分式的加减教案
分式1x2-3x与2x2-9的最简公分母是________.解析:∵x2-3x=x(x-3),x2-9=(x+3)(x-3),∴最简公分母为x(x+3)(x-3).方法总结:最简公分母的确定:最简公分母的系数,取各个分母的系数的最小公倍数;字母及式子取各分母中所有字母和式子的最高次幂.“所有字母和式子的最高次幂”是指“凡出现的字母(或含字母的式子)为底数的幂的因式选取指数最大的”;当分母是多项式时,一般应先因式分解.【类型二】 分母是单项式分式的通分通分.(1)cbd,ac2b2;(2)b2a2c,2a3bc2;(3)45y2z,310xy2,5-2xz2.解析:先确定最简公分母,找到各个分母应当乘的单项式,分子也相应地乘以这个单项式.解:(1)最简公分母是2b2d,cbd=2bc2b2d,ac2b2=acd2b2d;(2)最简公分母是6a2bc2,b2a2c=3b2c6a2bc2,2a3bc2=4a36a2bc2;(3)最简公分母是10xy2z2,45y2z=8xz10xy2z2,310xy2=3z210xy2z2,5-2xz2=--25y210xy2z2.

北师大初中八年级数学下册同分母分式的加减教案
解析:(1)先把第二个分式的分母y-x化为-(x-y),再把分子相加减,分母不变;(2)先把第二个分式的分母a-b化为-(b-a),再把分子相加减,分母不变.解:(1)原式=2x2-3y2x-y-x2-2y2x-y=2x2-3y2-(x2-2y2)x-y=x2-y2x-y=(x+y)(x-y)x-y=x+y;(2)原式=2a+3bb-a-2bb-a-3bb-a=2a+3b-2b-3bb-a=2a-2bb-a=-2(b-a)b-a=-2.方法总结:分式的分母互为相反数时,可以把其中一个分母放到带有负号的括号内,把分母化为完全相同.再根据同分母分式相加减的法则进行运算.三、板书设计1.同分母分式加减法法则:fg±hg=f±hg.2.分式的符号法则:fg=-f-g,-fg=f-g=-fg.本节课通过同分母分数的加减法类比得出同分母分式的加减法.易错点一是符号,二是结果的化简.在教学中,让学生参与课堂探究,进行自主归纳,并对易错点加强练习.从而让学生对知识的理解从感性认识上升到理性认识.

北师大初中八年级数学下册线段的垂直平分线教案
∵∠DAE=∠DAF,∠AED=∠AFD,AD=AD,∴△ADE≌△ADF,∴AE=AF,DE=DF,∴直线AD垂直平分线段EF.方法总结:当一条直线上有两点都在同一线段的垂直平分线上时,这条直线就是该线段的垂直平分线,解题时常需利用此性质进行线段相等关系的转化.三、板书设计1.线段的垂直平分线的性质定理线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段的垂直平分线的判定定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因此本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对线段垂直平分线性质定理的逆定理理解不透彻,还需在今后的教学和作业中进一步进行巩固和提高.

北师大初中八年级数学下册一元一次不等式的解法教案
方法总结:已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集唯一性列方程求字母的值.解题过程体现了方程思想.三、板书设计1.一元一次不等式的概念2.解一元一次不等式的基本步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)两边都除以未知数的系数.本节课通过类比一元一次方程的解法得到一元一次不等式的解法,让学生感受到解一元一次不等式与解一元一次方程只是在两边都除以未知数的系数这一步时有所不同.如果这个系数是正数,不等号的方向不变;如果这个系数是负数,不等号的方向改变.这也是这节课学生容易出错的地方.教学时要大胆放手,不要怕学生出错,通过学生犯的错误引起学生注意,理解产生错误的原因,以便在以后的学习中避免出错.

北师大初中八年级数学下册一元一次不等式组的解法及应用教案
安装及运输费用为600x+800(12-x),根据题意得4000x+3000(12-x)≤40000,600x+800(12-x)≤9200.解得2≤x≤4,由于x取整数,所以x=2,3,4.答:有三种方案:①购买甲种设备2台,乙种设备10台;②购买甲种设备3台,乙种设备9台;③购买甲种设备4台,乙种设备8台.方法总结:列不等式组解应用题时,一般只设一个未知数,找出两个或两个以上的不等关系,相应地列出两个或两个以上的不等式组成不等式组求解.在实际问题中,大部分情况下应求整数解.三、板书设计1.一元一次不等式组的解法2.一元一次不等式组的实际应用利用一元一次不等式组解应用题关键是找出所有可能表达题意的不等关系,再根据各个不等关系列成相应的不等式,组成不等式组.在教学时要让学生养成检验的习惯,感受运用数学知识解决问题的过程,提高实际操作能力.
道德与法治八年级下册理解权利义务2作业设计
本单元在整册教材中起到了承前启后的作用:第一单元《坚持宪法至上》主 要是培养学生的宪法意识,为后面的内容打下思想基础,通过本单元的学习,让 学生进一步认识宪法规定的公民基本权利和基本义务,帮助学生树立正确的权利 观和义务观,是对第一单元内容的深入和延伸;第三单元《人民当家做主》主要 是帮助学生更多的了解我国基本制度和国家机关,鼓励学生积极参与政治生活, 增强对国家的认同感和主人翁意识,学生需要学会正确行使公民的政治权利和自 由,因此,本单元又为第三单元内容的学习打下基础,作好铺垫。其中,第三课主要介绍公民的基本权利、如何正确行使权利及公民维权的途径,帮助学生树立正确的权利观;第四课主要介绍公民的基本义务、如何自觉履 行义务及违反义务须承担的责任,并在两课的基础上总结权利和义务的关系,帮 助学生树立正确的义务观,最终形成“权责一致”的观念。
道德与法治八年级下册理解权利义务4作业设计
某小区突发火情。消防中队接警后迅速赶来, 但由于沿途不少车辆乱停放堵 住道路, 消防车无法顺利进入小区。危急时刻, 小区一名热心大姐奋力呼救, 号 召周围居民配合物业人员一起用人力将沿途车辆一一搬开, 这才让消防车顺利抵 达起火楼栋,经过及时疏散,无人员伤亡。某校八(2)班以上述新闻为背景,组织一次以“依法行使权利,让生命通 道畅通”为主题的社会实践活动。请你参与其中。 (1)调查组的同学在某小区发现有一辆私家车占用了消防通道。联系车主后, 该车主说: “我自己的车, 想停哪儿就停哪儿, 哪有那么多火灾! ”请你从“权 利与义务的关系”的角度对其进行劝说该如何处理好权利和义务的关系。①公民的权利与义务相互依存、相互促进。 ②公民既是法定权利的享有者, 又是法定义务的承担者。 ③我们不仅要增强权利意识, 依法行使权利, 而且要增 强义务观念, 自觉履行法定的义务。因此, 作为小区居民, 我们在依法行使停车 权利的同时也要自觉履行维护小区消防安全的义务。
道德与法治八年级下册理解权利义务6作业设计
1.【解析】根据教材所学,依法治国要求全民守法,正确行使权利,自觉履行义务, A项没有履行依法纳税的义务,排除; B项没有履行服兵役的义务,排除;C项侵害救火英雄的名誉权,是一种违法行为,要承担相应的法律责任,故排除;D项自觉履行了维护国家安全和利益的义务,故符合题意。【答案】D2.【解析】该题考查公民的权利和义务的关系; 依据课本内容,公民的权利和义务是一致的。公民的权利和义务是密不可分的, 没有无义务的权利,也没有无权利的义务;题干中“不愿履行或轻视义务”割裂了权利与义务的关系,没有树立起正确的权利义务观念。 所以A项正确; BCD错误。【答案】A。3. 【解析】本题主要考查遵守宪法和法律这一公民基本义务。遵守和维护社会秩序是这一基本义务的具体要求,不服从国家疫情封控管理属于扰乱社会秩序的违法行为, 要承担一定的【答案】(1) 劝阻爸爸。(2) 自觉维护社会秩序, 依法履行公民义务, 法律要求的必须做,禁止做的坚决不做,否则就会受到法律制裁。

道德与法治八年级下册理解权利义务7作业设计
②积极参与国家事务和社会事务的管理③在享有劳动权利的同时,也履行了劳动的义务④既获得了劳动报酬,也为国家和社会作出了贡献 A.①② B.②③ C.①④ D.③④11.2020 年 6 月 19 日,国家林业和草原局、农业农村部发布通知,就《国家重点 保护野生动物名录》公开征求意见。画眉、啄木鸟、田螺等被增列入名录中,55 个鲸豚类和猛禽类等物种保护等级升级。作为中学生,保护野生动物是:( ) A.法律禁止做的,我们坚决不做 B.法律要求做的,我们必须去做C.道德要求做的,我们积极去做 D. 自觉自愿行为,可做也可不做 12.遇到交通肇事,不按照正常程序处理,而是采取极端的方式解决。陕西省榆 林市公安局榆阳分局镇川派出所,对涉嫌非法入侵他人住宅的 5 名嫌疑人刑拘。 这表明:( )①公民的住宅不受侵犯②禁止非法搜查或者非法侵入公民的住宅③公民权利如果受到损害,要懂得依照法定程序维护权利④我们在行使自由和权利的时候,不得损害其他公民的合法的自由和权利
道德与法治八年级下册理解权利义务作业设计
4.阅读材料,回答问题:疫情防控期间,一方面,公民面临着被感染的风险,有权获得政府和社会组 织提供的专业服务与保障。为此,国家有关部门出台了免除个人医疗费用负担的 政策,让广大患者消除了疾病治疗的后顾之忧。另一方面,公民也应当成为疫情 防控中的责任主体之一,依法履行自己的义务,如实报告自己的健康状况,配合 相关管理部门做好居家隔离。(1)结合材料,分析公民行使权利与履行义务之间的关系。(2)作为青少年,我们应该如何履行法律义务?5. 阅读材料,回答问题:2021年3月1日,《中小学教育惩戒规则(试行)》(以下简称“《规 则》”)正式施行。《规则》指出,学生有下列情形之一,学校及其教师应当予 以制止并进行批评教育,确有必要的,可以实施教育惩戒:(一)故意不完成教 学任务要求或者不服从教育、管理的;(二)扰乱课堂秩序、学校教育教学秩序 的;(三)吸烟、饮酒,或者言行失范违反学生守则的。

道德与法治八年级下册人民当家作主作业设计
①坚持依法行政,维护公平正义②严格遵循诉讼程序,加强立法③司法过程和结果都要合法、公正④坚持以事实为根据,以法律为准绳A.②④ B.②③ C.③④ D.①②3.疫情防控期间,某地检察院充分发挥检察职能,与公安机关等部门加强协作, 提前介入涉疫案件侦查,切实保障人民群众合法权益,全力维护疫情期间社会稳 定。由此可见 ( )①人民检察院是我国的法律监督机关②公安机关是我国的审判机关③公平正义需要法治的保障④人民检察院接受政府的领导和约束A.①② B.①③ C.②③ D.②④(二) 非选择题4. 探究与分享:结合所学知识,与同学讨论探究,回答下列问题。案例反思:2017 年 4 月 20 日,最高人民法院、中央电视台联合公布 2016 年推动法治进程十大案件评选结果,聂某被宣判无罪案等十大案件入选。1995 年 3 月,石家庄中院一审判处聂某死刑,同时判处赔偿受害人家属丧葬费等计 2000 元。1995 年 4 月 27 日,聂某被执行死刑。2016 年 12 月 2 日,最高人民法 院第二巡回法庭宣告撤销原审判决,改判聂某无罪。2017 年 3 月,聂某家属获 268.13991 万元国家赔偿。思考:如何才能避免这种错案的发生?
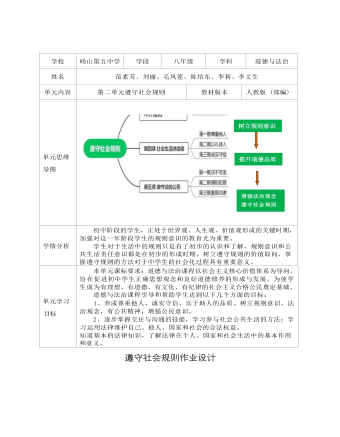
道德与法治八年级下册遵守社会规则作业设计
作业设计是老师布置给学生学习任务的设计,是教学设计的有机组 成部分。它以学习目标为起点,以学习内容为依托,以学习评价为保障, 以发展学生素养为最高标准。作业设计的要素包括作业内容、时间要求、 设计意图、作业分析及作业评价。我们八年级道德与法治组将单元作业 设计为三部分,第一部分是课时作业,本部分通过设置习题和活动,达 道巩固知识立德树人的目标。第二部分是单元作业,主要是为了检测学 生是否达到了单元学习目标,这部分重点考查学生对基础知识的掌握情 况。第三部分是特色作业,增强家国情怀,提高主人翁意识,更加注重 学生的能力提升。进入八年级,知识内容不断加深,同学们在学习方面面临着更大的 挑战,一部分学生因此产生畏难情绪,感觉学习吃力,如果在作业设置 方面,设置的作业量过大或过难,容易让学生彻底失去学习的兴趣,从 而放弃学习。

人教版新课标小学数学五年级下册设计镶嵌图案教案
师:同学们,在四年级的时候,我们已经了解了图形的密铺,请你说一说,什么是图形的密铺?(没有重叠、没有空隙地铺在平面上,就是密铺。)师:图形的密铺又可以叫做镶嵌,以上四个图片,都是由哪些基本图形密铺(镶嵌)而成的呢?(请学生边指边说。)师:还有哪些图形也可以镶嵌?(学生可能回答:三角形,平行四边形,梯形,菱形,正六边形,……)师:今天就请你发挥一下想象力,设计一些与众不同的镶嵌图形。[设计意图说明:学生在四年级已经初步了解了图形的密铺(镶嵌)现象,四幅图片是四年级下册教材《三角形》单元中《密铺》内容中的原图。本单元在此基础上,通过数学游戏拓展镶嵌图形的范围,让学生用图形变换设计镶嵌图案,进一步感受图形变换带来的美感以及在生活中的应用。]二、新授探究一:利用平移变换设计镶嵌图形

人教版新课标小学数学五年级下册分数的意义和性质教案
6. 本题是一道实际应用的题,可以结合生活实际举例,在举例中进一步认识分数。7. (读作八分之一)表示把人的身高看作单位“1”,头部的高度占整个身高的 ; (读作五分之三)表示把整个长江的干流看作单位“1”,受污染的部分占整个长江干流的 ; (读作十分之三)表示把死海表层的水看作单位“1”,含盐量占死海表层水的 。8. 读作六分之一, 读作七分之二, 读作是十五分之四, 读作十八分之十一, 读作一百分之七。它们的分数单位分别是: 、 、 、 、 。9. 本题有两个知识点:一是根据分数的意义涂色,是把12个苹果平均分成了2份,1份有6个苹果; 是把12个苹果平均分成了3份,1份有4个苹果; 是把12个苹果平均分成了4份,1份有3个苹果; 是把12个苹果平均分成了6份,1份有2个苹果; 是把12个苹果平均分成了12份,1份有1个苹果。二是在涂色中感受平均分成的份数越多,每一份越少,也可以说随着分母的增大,几分之一所表示的苹果个数,从 的6个到 的1个,相应地在减少。

人教版新课标小学数学五年级下册粉刷围墙教案
(3)按每千克涂料粉刷3.5 m2计算,可求出共需要涂料:1600÷3.5≈460(千克);(4)根据涂料的型号及费用,选择合适的涂料。师:选择涂料时,要考虑很多因素,如价格、耐用期、消费心理、环保等,要怎么选择呢?学生可以把几种涂料进行对比,一起讨论决定,同时学会在交流中理解接纳别人较好的建议:如:A型,优点:价格便宜,需要19桶,总共才5700元;缺点:耐用期太短,两年后又要重新粉刷;B-1型和B-2型,虽然桶装量不同,但价格和耐用期都处在中游水平;C型和D型,优点:耐用期长,最划算;缺点:价格太高,不符合人们的消费心理,也不可能持续那么长时间,至少5年就要更换一下样子。综合以上价格、耐用期、消费心理,选择B-1或B-2型比较划算。而这两种比较来看,B-2型更便宜一些,所以,最后确立用B-2型涂料。

人教版新课标小学数学五年级下册分数的加法和减法教案
二、 教学目标1.理解分数加减法的算理,掌握分数加减法的计算方法,并能正确地计算出结果。2.理解整数加法的运算定律对分数加法仍然适用,并会运用这些运算定律进行一些分数加法的简便运算,进一步提高简算能力。 3.体会分数加减运算在生活、生产中的广泛应用。三、学情分析五年级的学生已有一定的生活经验,对数学的神秘感有了更强的好奇心。因此,结合分数加减的学习内容适当补充一些数学史料,可使学生的好奇转化为探究欲,促其学习数学兴趣的提高,并逐步形成良好的探究习惯。因此,教学时,应重视教材提供的两个涉及数学文化的阅读材料的学习。在此基础上,再补充一些相关的学习材料。四、教学重点、难点重点:分数加减法的计算方法难点:引导学生体会理解不同算法的思路。

人教版新课标小学数学五年级下册因数与倍数教案
因此,本套教材中删去了“整除”的数学化定义,而是借助整除的模式na=b直接引出因数和倍数的概念。在本册教材中,由于允许学生采用多样的方法求最大公因数和最小公倍数,分解质因数也失去了其不可或缺的作用,同时,也是为了减少这一单元的理论概念,教材不再把它作为正式教学内容,而是作为一个补充知识,安排在“你知道吗?”中进行介绍。由于这部分内容较为抽象,很难结合生活实例或具体情境来进行教学,学生理解起来有一定的难度。在过去的教学中,一些教师往往忽视概念的本质,而是让学生死记硬背相关概念或结论,学生无法理清各概念间的前后承接关系,达不到融会贯通的程度。再加上有些教师在考核时使用一些偏题、难题,导致学生在学习这部分知识时觉得枯燥乏味,体会不到初等数论的抽象性、严密性和逻辑性,感受不到数学的魅力。所以在教学中应注意以下两点: (1)加强对概念间相互关系的梳理,引导学生从本质上理解概念,避免死记硬背。(2)由于本单元知识特有的抽象性,教学时要注意培养学生的抽象思维能力。








