-
北师大初中七年级数学上册从三个方向看物体的形状教案1
1．经历从不同方向观察物体的活动过程，发展空间观念．2．在观察的过程中，初步体会从不同方向观察同一物体可能看到不同的形状．3．能识别从三个方向看到的简单物体的形状，会画立方体及简单组合体从三个方向看到的形状，并能根据看到的形状描述基本几何体或实物原型．一、情境导入观察图中不同方向拍摄的庐山美景．你能从苏东坡《题西林壁》诗句：“横看成岭侧成峰，远近高低各不同．不识庐山真面目，只缘身在此山中．”体验出其中的意境吗？你能挖掘出其中蕴含的数学道理吗？让我们一起探索新知吧！二、合作探究探究点一：从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的，从上面看到的平面图形是()解析：这个几何体从上面看，共有2行，第一行能看到3个小正方形，第二行能看到2个小正方形．故选D.
北师大初中七年级数学上册从三个方向看物体的形状教案2
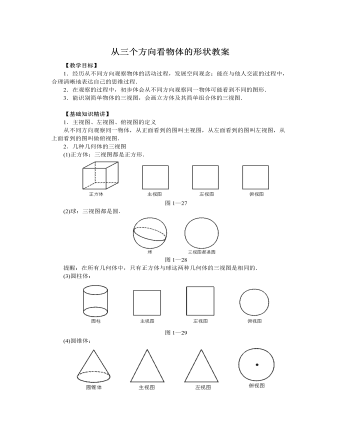
【教学目标】1．经历从不同方向观察物体的活动过程，发展空间观念；能在与他人交流的过程中，合理清晰地表达自己的思维过程．2．在观察的过程中，初步体会从不同方向观察同一物体可能看到不同的图形．3．能识别简单物体的三视图，会画立方体及其简单组合体的三视图．【基础知识精讲】1．主视图、左视图、俯视图的定义从不同方向观察同一物体，从正面看到的图叫主视图，从左面看到的图叫左视图，从上面看到的图叫做俯视图．2．几种几何体的三视图(1)正方体：三视图都是正方形．圆锥的主视图、左视图都是三角形，而俯视图的图中有一个点表示圆锥的顶点，因为从上往下看圆锥时先看到圆锥的顶点，再看到底面的圆．3．如何画三视图 当用若干个小正方体搭成新的几何体，如何画这个新的几何体的三视图？
北师大初中七年级数学下册三角形的内角和教案
解：∵CE⊥AF，∴∠DEF＝90°，∴∠EDF＝90°－∠F＝90°－40°＝50°.由三角形的内角和定理得∠C＋∠DBC＋∠CDB＝∠F＋∠DEF＋∠EDF，又∵∠CDB＝∠EDF，∴30°＋∠DBC＝40°＋90°，∴∠DBC＝100°.方法总结：本题主要利用了“直角三角形两锐角互余”的性质和三角形的内角和定理，熟记性质并准确识图是解题的关键．三、板书设计1．三角形的内角和定理：三角形的内角和等于180°.2．三角形内角和定理的证明3．直角三角形的性质：直角三角形两锐角互余．本节课通过一段对话设置疑问，巧设悬念，激发起学生获取知识的求知欲，充分调动学生学习的积极性，使学生由被动接受知识转为主动学习，从而提高学习效率．然后让学生自主探究，在教学过程中充分发挥学生的主动性，让学生提出猜想．在教学中，教师通过必要的提示指明学生思考问题的方向，在学生提出验证三角形内角和的不同方法时，教师注意让学生上台演示自己的操作过程和说明自己的想法，这样有助于学生接受三角形的内角和是180°这一结论
北师大初中八年级数学下册分式方程的应用教案
解：(1)设第一次购买的单价为x元，则第二次的单价为1.1x元，根据题意得14521.1x－1200x＝20，解得x＝6.经检验，x＝6是原方程的解．(2)第一次购买水果1200÷6＝200(千克)．第二次购买水果200＋20＝220(千克)．第一次赚钱为200×(8－6)＝400(元)，第二次赚钱为100×(9－6.6)＋120×(9×0.5－6.6)＝－12(元)．所以两次共赚钱400－12＝388(元)．答：第一次水果的进价为每千克6元；该老板两次卖水果总体上是赚钱了，共赚了388元．方法总结：本题具有一定的综合性，应该把问题分解成购买水果和卖水果两部分分别考虑，掌握这次活动的流程．三、板书设计列分式方程解应用题的一般步骤是：第一步，审清题意；第二步，根据题意设未知数；第三步，根据题目中的数量关系列出式子，并找准等量关系，列出方程；第四步，解方程，并验根，还要看方程的解是否符合题意；最后作答．
北师大初中八年级数学下册分式方程的概念及列分式方程教案
探究点二：列分式方程某工厂生产一种零件，计划在20天内完成，若每天多生产4个，则15天完成且还多生产10个．设原计划每天生产x个，根据题意可列分式方程为()A.20x＋10x＋4＝15 B.20x－10x＋4＝15C.20x＋10x－4＝15 D.20x－10x－4＝15解析：设原计划每天生产x个，则实际每天生产(x＋4)个，根据题意可得等量关系：(原计划20天生产的零件个数＋10个)÷实际每天生产的零件个数＝15天，根据等量关系列出方程即可．设原计划每天生产x个，则实际每天生产(x＋4)个，根据题意得20x＋10x＋4＝15.故选A.方法总结：此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，找出题目中的等量关系，列出方程．三、板书设计1．分式方程的概念2．列分式方程本课时的教学以学生自主探究为主，通过参与学习的过程，让学生感受知识的形成与应用的价值，增强学习的自觉性，体验类比学习思想的重要性，然后结合生活实际，发现数学知识在生活中的广泛应用，感受数学之美.
北师大初中八年级数学下册分式方程的解法教案
【类型三】 分式方程无解，求字母的值若关于x的分式方程2x－2＋mxx2－4＝3x＋2无解，求m的值．解析：先把分式方程化为整式方程，再分两种情况讨论求解：一元一次方程无解与分式方程有增根．解：方程两边都乘以(x＋2)(x－2)，得2(x＋2)＋mx＝3(x－2)，即(m－1)x＝－10.①当m－1＝0时，此方程无解，此时m＝1；②方程有增根，则x＝2或x＝－2，当x＝2时，代入(m－1)x＝－10得(m－1)×2＝－10，m＝－4；当x＝－2时，代入(m－1)x＝－10得(m－1)×(－2)＝－10，解得m＝6，∴m的值是1，－4或6.方法总结：分式方程无解与分式方程有增根所表达的意义是不一样的．分式方程有增根仅仅针对使最简公分母为0的数，分式方程无解不但包括使最简公分母为0的数，而且还包括分式方程化为整式方程后，使整式方程无解的数．三、板书设计1．分式方程的解法方程两边同乘以最简公分母，化为整式方程求解，再检验．2．分式方程的增根(1)解分式方程为什么会产生增根；(2)分式方程检验的方法．
北师大初中八年级数学下册异分母分式的加减教案
分式1x2－3x与2x2－9的最简公分母是________．解析：∵x2－3x＝x(x－3)，x2－9＝(x＋3)(x－3)，∴最简公分母为x(x＋3)(x－3)．方法总结：最简公分母的确定：最简公分母的系数，取各个分母的系数的最小公倍数；字母及式子取各分母中所有字母和式子的最高次幂．“所有字母和式子的最高次幂”是指“凡出现的字母(或含字母的式子)为底数的幂的因式选取指数最大的”；当分母是多项式时，一般应先因式分解．【类型二】 分母是单项式分式的通分通分．(1)cbd，ac2b2；(2)b2a2c，2a3bc2；(3)45y2z，310xy2，5－2xz2.解析：先确定最简公分母，找到各个分母应当乘的单项式，分子也相应地乘以这个单项式．解：(1)最简公分母是2b2d，cbd＝2bc2b2d，ac2b2＝acd2b2d；(2)最简公分母是6a2bc2，b2a2c＝3b2c6a2bc2，2a3bc2＝4a36a2bc2；(3)最简公分母是10xy2z2，45y2z＝8xz10xy2z2，310xy2＝3z210xy2z2，5－2xz2＝－－25y210xy2z2.
北师大初中八年级数学下册同分母分式的加减教案
解析：(1)先把第二个分式的分母y－x化为－(x－y)，再把分子相加减，分母不变；(2)先把第二个分式的分母a－b化为－(b－a)，再把分子相加减，分母不变．解：(1)原式＝2x2－3y2x－y－x2－2y2x－y＝2x2－3y2－（x2－2y2）x－y＝x2－y2x－y＝（x＋y）（x－y）x－y＝x＋y；(2)原式＝2a＋3bb－a－2bb－a－3bb－a＝2a＋3b－2b－3bb－a＝2a－2bb－a＝－2（b－a）b－a＝－2.方法总结：分式的分母互为相反数时，可以把其中一个分母放到带有负号的括号内，把分母化为完全相同．再根据同分母分式相加减的法则进行运算．三、板书设计1．同分母分式加减法法则：fg±hg＝f±hg.2．分式的符号法则：fg＝－f－g，－fg＝f－g＝－fg.本节课通过同分母分数的加减法类比得出同分母分式的加减法．易错点一是符号，二是结果的化简．在教学中，让学生参与课堂探究，进行自主归纳，并对易错点加强练习．从而让学生对知识的理解从感性认识上升到理性认识.
北师大初中九年级数学下册弧长及扇形的面积教案
1．了解扇形的概念，理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用；(重点)2．通过复习圆的周长、圆的面积公式，探索n°的圆心角所对的弧长l＝nπR180和扇形面积S扇＝nπR2360的计算公式，并应用这些公式解决一些问题．(难点)一、情境导入如图是圆弧形状的铁轨示意图，其中铁轨的半径为100米，圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14，所以铁轨的长度l≈2×3.14×1004＝157(米). 如果圆心角是任意的角度，如何计算它所对的弧长呢？二、合作探究探究点一：弧长公式【类型一】 求弧长如图，某厂生产横截面直径为7cm的圆柱形罐头盒，需将“蘑菇罐头”字样贴在罐头侧面．为了获得较佳视觉效果，字样在罐头盒侧面所形成的弧的度数为90°，则“蘑菇罐头”字样的长度为()
北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元，获得的利润为y元，则定价为 元 ，每件利润为 元 ，每星期多卖 件，实际卖出 件。所以Y= 。（0<X<20）何时有最大利润，最大利润为多少元？比较以上两种可能，衬衣定价多少元时，才能使利润最大？☆ 归纳反思 ☆总结得出求最值问题的一般步骤：（1）列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围；（2）在自变量的取值范围内，运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形，设矩形面积是ym2,，则y与x之间函数关系式为 ，当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车，市场调查表明：当每辆车的日租金为300元时可全部租出；当每辆车的日租金提高10元时，每天租出的汽车会相应地减少4辆．问每辆出租车的日租金提高多少元，才会使公司一天有最多的收入？
北师大初中九年级数学下册图形面积的最大值1教案
如图所示，要用长20m的铁栏杆，围成一个一面靠墙的长方形花圃，怎么围才能使围成的花圃的面积最大？如果花圃垂直于墙的一边长为xm，花圃的面积为ym2，那么y＝x(20－2x)．试问：x为何值时，才能使y的值最大？二、合作探究探究点一：二次函数y＝ax2＋bx＋c的最值已知二次函数y＝ax2＋4x＋a－1的最小值为2，则a的值为()A．3 B．－1 C．4 D．4或－1解析：∵二次函数y＝ax2＋4x＋a－1有最小值2，∴a＞0，y最小值＝4ac－b24a＝4a（a－1）－424a＝2，整理，得a2－3a－4＝0，解得a＝－1或4.∵a＞0，∴a＝4.故选C.方法总结：求二次函数的最大(小)值有三种方法，第一种是由图象直接得出，第二种是配方法，第三种是公式法．变式训练：见《学练优》本课时练习“课堂达标训练” 第1题探究点二：利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值
关于端正的态度是学习的法宝的国旗下讲话
端正的态度是学习的法宝老师、同学们：大家早上好！今天我在国旗下讲话的内容是《端正的态度是学习的法宝》。俗话说：“宝剑锋从磨砺出，梅花香自苦寒来。”在学习上也是如此，那些学习上的佼佼者，都付出了比别人多的努力，今天就来谈谈学习的态度，因为态度决定一切。我觉得要做到三个“超越”。1． 超越自己，这个世界上最难战胜和超越的人不是别人，正是你自己，当你发现自己在一点一点改变时，你就超越自己了，只有超越自己，才可能超越别人。
小班谈话教案 我的一家人
2、引导幼儿围绕“我的一家人”这一话题进行谈话，使幼儿乐意参与个别交谈与集体谈话活动。3、培养幼儿爱家庭的情感，知道关心长辈，听大人的话。活动准备：1、实物玩具：小兔、狗、熊。2、大图片及每个幼儿一张“全家福”照片、篓子。3、录音机、磁带。4、让幼儿回家了解父母的工作及家庭成员之间的关系。 活动过程：1、创设谈话情境，引出谈话话题。（1）放录音《世上只有妈妈好》，教师带领幼儿边唱边动作。（2）请两位幼儿讲一讲“家里有谁”要求语句完整。师；小朋友家里除了妈妈以外，还有谁呢，谁愿意到前面来拿自己的照片讲给大家听，而且要把话说完整。教师利用实物投影，让幼儿看着画在讲，同时教师要重复幼儿的话练习幼儿说话的完整性。
关于做文明高中生的国旗下的讲话
遵守校纪校规，做文明高中生各位老师，各位同学：大家早上好！今天国旗下讲话的的题目是 “遵守校纪校规，做文明高中生”。日升月落，斗转星移，不觉间，我们已经走过十六七个春秋，匆匆的脚步，如水的岁月，冲淡我们许许多多美好的记忆，尘封许许多多精彩的往事。但对于我们，至真至诚地遵守校规，则是我们心中遵循的坚定信念。自觉养成遵纪守法的习性，是我们珍惜的道德底线，遵纪守法牢牢铭刻在我们的心间，伴随我们快乐健康成长。古人云："无规矩不成方圆。"马克思说："我们必须遵守组织的规矩，否则一切都将陷入污泥中。"国有国法，校有校规。这些法律规章是维系国家、学校的基本规则，国家要发展，学校要和谐，我们就要自觉遵守国法，自觉遵守校规。这是毫无疑义的。要自觉遵守校纪校规，做文明的学生，就要用智慧的双眼，清醒的头脑，理智的行为，看学校，看社会，去做事，去为人。我们还年轻，我们往往迷惘与清醒并存，我们要压抑着青春的激荡，要收敛年少的狂放，远离憧憬的诗行，抛弃感情的冲动，迈向理性，走向成熟。
《飞的更高》教案
教学过程一、创设情境导入。先弹奏一遍《飞得更高》的音乐，吸引同学们的兴趣。师：同学们以前有没有听过汪峰的歌曲？感觉它的风格是什么样的？（《怒放的生命》，摇滚型歌手）生：……师：同学们以前有没有听过这首歌？听完这首歌有什么样的感受？生：励志、向上、振奋……师：想象一下这首歌所呈现的画面。（歌曲像一条大河，缓缓流过，起初平静，时而急流时而狭窄，逐渐开阔。如同生命。听者会被带入一种境界，如同站在网中漫步一片辽阔的旷野，雄鹰在头顶的天空翱翔，令心中有一种欲望在疯长，无法遏止。）
大青树下的小学教案
《大青树下的小学》是统编教材小学语文三年级上册第一单元第一课。《大青树下的小学》是一篇精读课文，课文通过描写边疆的一所民族小学的孩子们幸福的学习生活，体现了祖国各民族之间的友爱和团结。课文层次清晰、段落分明。先写上学的路上和来学校的情景；再写上课时和下课后的情景，最后以自豪赞美的文字点题。学习本课我将引导学生通过对课文的整体把握和重点词句的理解，了解我国各民族儿童的友爱团结及他们幸福的学习生活，体会贯穿全文的自豪和赞美之情。
三年级语文花的学校教案
《花的学校》是一首优美而富有童趣的诗歌，作者用拟人手法，展开了丰富的想象。作者巧妙地从孩子的眼中叙出花儿们的活泼、可爱、美丽、向上，充满了儿童情趣。诗歌的语言和所描绘的情境很能调动学生相关的情感体验，激发他们的学习兴趣，使他们对学习内容产生亲近感。教学中我注重学生的朗读指导，读出花孩子的天真烂漫、活泼可爱、勇敢坚强、活泼向上、童真童趣。同时也注重培养学生的问题意识。课文的想象非常大胆、有趣、合理，可以结合课后练习题让学生进行想象力训练。
大班科学教案：食品的贮存
说明： 利用各种食品的方法来贮存食物，在我国有着悠久的历史，早在《诗经》中就记录以冰窖存物的方法。随着现代物质水平的提高，及科学技术的发展，贮存食物不仅仅为了保存食物，而更广泛地表现为口味的丰富、携带的方便，以及适应现代生活的需要。孩子们在日常生活中，也常常看到各种食物，，有的被贮存于真空包装袋中，有的浸泡在各类瓶瓶罐罐中，有的放在冰柜里，还有的悬挂在竹竿上。同样，孩子们也常有机会吃到这些经过特殊贮存或加工的食物。然而，对为什么要贮存食物，怎么来贮存食物却知之甚少。因此，“食物的贮存”这一活动旨在让孩子们在操作、谈论、比较中，了解粗浅的食物方法，知道贮存给现代生活所带来的种种好处，培养他们对生活小科学的探索兴趣，满足他们的好奇心。
大班科学教案：有趣的汁液
2、操作工具：塑料袋、剪刀、盘子、纱布、小铁锤、小木棍、抹布、棉签、图画纸、宣纸等。3、师用教具：隐形画范图一幅、电炉一个活动过程：一、引入导语：春天到了，春姑娘给我们送礼物来了。讨论：为什么你们觉得鲜花很漂亮？五颜六色的鲜花有什么用？小结：鲜花能美化环境，鲜花的汁液能绘画、染纸。二、幼儿进行尝试活动1、尝试活动⑴：导语：既然花汁能染纸，那花汁是怎样取得的呢？幼儿讨论并进行尝试活动（挤汁--染纸）2、尝试活动⑵：导语：春姑娘不仅给我们送来了鲜花，还送来了丰富的水果，水果除了好吃以外，它能画画吗？幼儿讨论并进行尝试活动（挤汁---用棉签沾果汁在图画纸上作画）小结：果汁能画画，但有的果汁干了以后，就什么也看不见。
大班科学教案：转动的陀螺
目标：1．对物体转动变化感兴趣，探索影响陀螺转动变化的一些因素。2．尝试在探索和比较中发现问题、分析问题。 准备：1．直径6厘米左右的红色塑料圆片(数量与幼儿人数相等)，在塑料片的中心处打一个小洞，刚好适合牙签通过。2．直径6厘米左右的黄色塑料圆片(数量与幼儿人数相等)，在塑料片的偏离中心处打一个小洞，刚好适合牙签通过。3．牙签(数量为幼儿人数的2~3倍)，棉签，纸盒，吸管，记录纸，笔。4．打印汉字“转动”。