-

幼儿园优秀课《鹅大哥出门》说课稿
一. 说设计思路 《鹅大哥出门》这个故事选用了小朋友生活中比较熟悉并喜欢的大白鹅为主要角色,讲述了一只大白鹅骄傲不懂礼貌的故事,特别是鹅大哥之前“红红的帽子,雪白的羽毛”和之后的“一只大黑鹅”对比这个情节既让人觉得有趣又符合幼儿的年龄特点,在生活中我们常常会看到一些自高自大的人,特别是现在独生子女较多,比较以我为中心,我觉得这个故事既符合幼儿的年龄特点又符合孩子们现在的心理而且也符合<纲要>中的教育要求,即教育幼儿使用礼貌语言与人交往,养成文明交往的习惯.

大班语言《鹅大哥出门》说课稿
一、说设计思路《鹅大哥出门》这个故事选用了小朋友生活中比较熟悉并喜欢的大白鹅为主要角色,讲述了一只大白鹅骄傲不懂礼貌的故事,特别是鹅大哥之前“红红的帽子,雪白的羽毛”和之后的“一只大黑鹅”对比这个情节既让人觉得有趣又符合幼儿的年龄特点,在生活中我们常常会看到一些自高自大的人,特别是现在独生子女较多,比较以我为中心,我觉得这个故事既符合幼儿的年龄特点又符合孩子们现在的心理而且也符合<纲要>中的教育要求,即教育幼儿使用礼貌语言与人交往,养成文明交往的习惯.二、说活动目标活动目标是教学活动的起点和归宿,对教育活动起导向作用。<纲要>语言领域中指出:发展幼儿语言的关键是创设一个是他们想说,敢说,喜欢说的环境。在新《纲要》中,活动教育提出了“幼儿园的教育活动,应以教师带领幼儿共同创设适应幼儿年龄特点的,丰富多彩的,引导幼儿在轻松愉快的心理氛围中,积极主动地去体验,实践、创造,促进幼儿身心和谐发展的一种教育活动。”因此,在整个活动中都以幼儿的自主参与活动为主,教师在活动中起一个引导者和支持者的作用,和孩子共同活动感受,我从认知、能力和情感三方面提出了本次活动的目标。1. 认知上:使幼儿在理解故事内容的基础上,初步学会复述故事,丰富词汇“神气、乐滋滋”2. 能力上:积极参与故事情节的讨论,愿意大胆表达自己的想法。3. 情感上:懂得不能骄傲,不能欺负弱小的道理体验骄傲自大带来的烦恼根据目标,在活动中,我把在游戏情节中理解故事内容,懂得不能骄傲不欺负弱小的道理设为教学重点,根据大班幼儿的语言发展情况,用完整的语言复述故事设为难点。三、说活动准备为了此次活动的组织符合幼儿的学习方式和特点,注重综合性、趣味性、活动性的协调统

大班诗歌《大自然的话》说课稿
我选择的说课的科目是语言,课题内容是诗歌《大自然的话》,教材选自江苏幼儿园综合活动教师指导用书。这首诗歌科学知识趣味性很强,可以借机培养幼儿观察大自然的兴趣,进而培养幼儿热爱大自然的美好情感。要想让幼儿理解和体会到诗歌中的内容,感受诗歌的美,就必须对诗歌中提到的大自然的景象有所了解,这是理解这首诗歌的知识基础也是本次活动的知识点。我在课前利用了散步活动、谈话活动引导幼儿观察认识大自然有规律的变化,让幼儿了解四季的变化特征,动植物的变化,让幼儿亲身感受生活中大自然的美,为诗歌教学的开展奠定了情感基础。根据大班幼儿的年龄及心理特点,从情感教育、能力培养、知识三个方面认真制定了本次活动的教学目标。具体是:1、欣赏诗歌,初步感知诗歌的语言和结构等艺术特点。2、在理解诗歌内容的基础上尝试仿编。3、有欣赏、了解大自然的浓厚兴趣,体验人和大自然的亲情。

大班美工《阳澄湖大闸蟹》说课稿
阳澄湖大闸蟹是我镇的特产,孩子们对螃蟹很感兴趣,时值金秋、螃蟹上市,孩子们的话题也离不开谈论螃蟹的有关事情。于是我们科研组根据幼儿的兴趣设计了有关螃蟹的一系列活动。也结合我园开展的市级课题“开发本土教育资源,构建园本课程的实践研究”实施,主动积极地进行一系列、多样化的活动,从中掌握正确的学习方法,体验宽松学习的乐趣。经过收集实物、图片、照片等资料,孩子们对螃蟹有了进一步的理解、掌握了相关的知识与外形特征,同时还萌发了各种表现螃蟹形态的欲望。在系列活动中,也制作过螃蟹,但是幼儿余兴未了;于是设计了利用多种材料制作“阳澄湖大闸蟹”这一手工活动。1、看录象(帮助幼儿回忆秋季阳澄湖大闸蟹丰收的景象和人们欢庆的场面,为活动的开展作情感铺垫)2、请小朋友来介绍一下螃蟹是什么样子的?(幼儿自由说说:由于大闸蟹是我镇的特产和骄傲,所以幼儿能说出螃蟹的特征,圆圆的身体、身体两旁各有四条腿、前面有二只大钳子、还有两只眼睛。)

大班绘本《狼大叔的红焖鸡》说课稿
整个活动过程清晰,安排合理。教师从观察封面导入,借助提问边引导幼儿观察画面,让他们从狼大叔的眼神、动作、神情中去捕捉它随着故事的发展而不时变化的心情、心理。并采用多种手段引领幼儿阅读,猜测除了吃再没有别的爱好的狼大叔在发现一只母鸡时的激动和窃喜以及心理变化;体会当狼大叔改变主意想把母鸡养肥了再吃的时的沾沾自喜;体会大灰狼天天偷偷给母鸡送美味佳肴时的满怀希望;感受大灰狼以为时机成熟,准备捉母鸡下锅时的急切以及在门外偷窥却被母鸡称为“亲爱的狼大叔”当作恩人被热情迎进门时的尴尬,哭笑不得;感悟大灰狼被母鸡的孩子亲了100口时无奈和甜蜜以及在吃了母鸡招待它的丰盛晚餐之后,打算着再给小鸡们送100个小饼干时的娇憨可爱。这一部分金老师不仅注重创造宽松的教学氛围,积极与幼儿互动,边讲边提问,引导幼儿边听边思考,促进幼儿和教师之间的双向互动效果,同时在这一过程中金老师的引导既能关注到全体,又能兼顾到个别,由浅入深,有效激发幼儿思考,发挥幼儿的想象力,显示了幼儿的主体地位。让幼儿体会到讲述的快乐,从而在不知不觉中锻炼了语言的表达能力。

大班体育《战胜大灰狼》说课稿
二.教学目标的制定废旧的自行车轮胎看起来并不起眼,但对于孩子的来说却是一件不可多得的宝贝。它的可玩、可创造、可变形、将在活动中带给孩子极大的乐趣。素质教育的重点之一是孩子创新意识和创造能力的培养。在此次活动设计中,我将为孩子们创造各种有趣的情境,利用手中的废旧自行车轮胎,让孩子创想出各种不同的玩胎方式,启发他们的发散性思维,起到“一物多玩”,“一物多用”的效果。在富有创造性的故事情节中,幼儿也同样感受着这样一种熏陶:那就是不管敌人有多可怕,只要我们积极锻炼身体,团结合作,勇敢对“敌”,我们必定会取得最后的胜利。因此,根据器材本身和当今“二期课改”的精神要求,我为此活动制定了以下目标:1.通过尝试自行车轮胎的各种玩法,发展幼儿走、跑、跳、钻爬等基本动作,发展幼儿的想象能力和创造能力。2.让幼儿自定比赛规则和玩法,发挥幼儿主动学习的精神。3.通过激烈的比赛,发挥幼儿的竞争意识及不怕苦、不怕累,勇敢对敌的精神。三.教学活动设计和组织新颖的体育活动设计,对幼儿具有极大的挑战性和吸引力,它能大大地提高幼儿的探索欲望,激发幼儿对活动新形势的喜爱。整个故事情节叙述了小兔如何被大灰狼欺负,如何努力学本领、锻炼身体,最终齐心协力、打败大灰狼的故事。游戏开始部分,小兔自由自在地草地上蹦跳,听到妈妈(有老师扮演)在叫“狼来了”,小兔迅速地跑到房子(轮胎)内抱成一团,尽量不要掉到房子外,以免被大灰狼(由另一幼儿扮演)抓走。当大灰狼走时,小兔又重新回到草地,但狡猾的大灰狼却会每次来悄悄地偷走了他们的一座房子。到下一次狼来袭击时,因为房子数量的逐渐减少,就给小兔增添了躲藏的难度,这就要求小兔要迅速地调整所站的位置,以站下更多的小兔。虽然这只是一个小小的热身游戏,但却在无形中培养了他们关爱他人,团结协作和谦让宽容的精神。

北师大版小学数学五年级下册《复式折线统计图》说课稿
一、说教材:1.说课内容:本节课的内容是北师大版5年级数学下册第8单元的《复式折线统计图》。2.教材分析:这节课的内容是在学生学习了单式折线统计图和复式条形统计图的基础上教学的。这节课的内容包括制作复式折线统计图的必要性、制作方法以及对这种统计图的分析预测。教材在设计中,主要突出了以下两个方面:(1)对比。为了方便比较甲、乙两个城市各月的降水量,把两个单式折线统计图画在同一幅图上,变成复式折线统计图。让学生感受出现复式折线统计图的必要性和其带来的好处。(2)读图。通过对复式折线统计图中两条折线升降的分析,对数据进行合理的预测,这也是课标的要求。3.教材的地位和作用:本课的学习,不但可以用来解决日常生活中的一些实际问题,也是今后学习更多其他统计图的重要基础。

北师大版小学数学六年级上册《扇形统计图》说课稿
一、教材分析:教材的地位和作用新课标教材中《数据处理》安排在小学一至六年级的各册教材中。在第一学段(一至三年级)中,学生将数据统计过程有所体验,学习一些简单的收集、整理和描述数据的方法;在第二学段(四至六年级)中,学生将经历简单的数据统计过程,进一步学习收集、整理和描述数据的方法,并根据数据分析的结果做出简单的判断与预测。在第二学段主要学习条形统计图、折线统计图、扇形统计图,主要使学生掌握各种统计图的优劣,经历运用数据描述信息、作出推断的过程,发展统计观念。有关统计图的认识,小学阶段主要认识条形统计图、折线统计图和扇形统计图。考虑到扇形统计图在日常生活中的广泛应用,《标准》把它作为必学内容安排在本单元。本单元是在前面学习了条形统计图和折线统计图的特点和作用的基础上进行教学的。主要通过熟悉的事例使学生体会到统计的实用价值。

北师大版小学数学六年级上册《统计图的选择》说课稿
一、教材分析1.教材的地位和作用本节教材是北师大版六年级数学上册第5章《数据的收集与整理》第3节的内容,这一章是《全日制义务教育数学课程标准(实验稿)》第三学段“统计与概率”部分的第一章,也是基础章节。它让学生经历数据的收集、整理、描述的过程,体会适当选择统计图表对描述实际问题的作用,为以后进一步学习统计的有关知识打下基础2.学情分析学生在此之前已经在小学阶段学习过有关统计图表的知识,对三种统计图也有了一定的认识和感知,会画三种统计图,但是对于究竟如何选取适当的统计图去说明一些具体实际问题还存在一定困难,所以本节内容主要是让学生对三种统计图各自的特点和优势有一定的认识。3.教材重难点根据对教材的研读和学生学情的分析,结合新课标对本节的要求,特将本节的重难点确定如下:

北师大初中数学九年级上册一元二次方程的解及其估算2教案
探索1:上节我们列出了与地毯的花边宽度有关的方程。地毯花边的宽x(m),满足方程 (8―2x)(5―2x)=18也就是:2x2―13x+11=0你能估算出地毯花边的宽度x吗?(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业

北师大初中数学九年级上册一元二次方程2教案
三、课堂检测:(一)、判断题(是一无二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1. 5x2+1=0 ( ) 2. 3x2+ +1=0 ( )3. 4x2=ax(其中a为常数) ( ) 4.2x2+3x=0 ( )5. =2x ( ) 6. =2x ( ) (二)、填空题.1.方程5(x2- x+1)=-3 x+2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.2.如果方程ax2+5=(x+2)(x-1)是关于x的一元二次方程,则a__________.3.关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程。四、学习体会:五、课后作业

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?

北师大初中七年级数学上册截一个几何体教案1
解析:当截面与轴截面平行时,得到的截面的形状为长方形;当截面与轴截面斜交时,得到的截面的形状是椭圆;当截面与轴截面垂直时,得到的截面的形状是圆,所以截面的形状不可能是三角形.故选A.方法总结:用平面去截圆柱时,常见的截面有圆、椭圆、长方形、类似于梯形、类似于拱形等.探究点三:截圆锥问题一竖直平面经过圆锥的顶点截圆锥,所得到的截面形状与下图中相同的是()解析:经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线.如图,由图可知得到的截面是一个等腰三角形.故选B.方法总结:用平面去截圆锥,截面的形状可能是三角形、圆、椭圆等.三、板书设计教学过程中,强调学生自主探索和合作交流,经历操作、抽象、归纳、积累等思维过程,从中获得数学知识与技能,发展空间观念和动手操作能力,同时升华学生的情感态度和价值观.
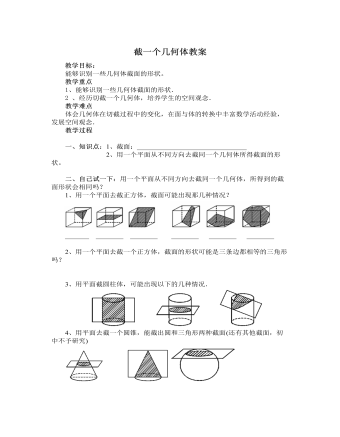
北师大初中七年级数学上册截一个几何体教案2
[例3]、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是_________。四、巩固强化:1、一个正方体的截面不可能是( )A、三角形 B、梯形 C、五边形 D、七边形2、用一个平面去截五棱柱,边数最多的截面是_______形.3*、用一个平面去截几何体,若截面是三角形,这个几何体可能是__________________________________________________.4*、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如虹截面是三角形呢?5*、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?6*、几何体中的圆台、棱锥都是课外介绍的,所以我们就在这个栏目里继续为大家介绍这两种几何体的截面.(1)圆台用平面截圆台,截面形状会有_____和_______这两种较特殊图形,截法如下:

北师大初中数学八年级上册单个一次函数图象的应用2教案
(1)用简洁明快的语言概括大意,不能超过200字;(2)图表中能确定的数值,在故事叙述中不得少于3个,且要分别涉及时间、路和速度这三个量.意图:旨在检测学生的识图能力,可根据学生情况和上课情况适当调整。说明:练习注意了问题的梯度,由浅入深,一步步引导学生从不同的图象中获取信息,对同学的回答,教师给予点评,对回答问题暂时有困难的同学,教师应帮助他们树立信心。第四环节:课时小结内容:本节课我们学习了一次函数图象的应用,在运用一次函数解决实际问题时,可以直接从函数图象上获取信息解决问题,当然也可以设法得出各自对应的函数关系式,然后借助关系式完全通过计算解决问题。通过列出关系式解决问题时,一般首先判断关系式的特征,如两个变量之间是不是一次函数关系?当确定是一次函数关系时,可求出函数解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.

北师大初中数学八年级上册单个一次函数图象的应用1教案
方法总结:要认真观察图象,结合题意,弄清各点所表示的意义.探究点二:一次函数与一元一次方程一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为()A.x=-1B.x=2C.x=0D.x=3解析:首先由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,从而可得出一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1,故选A.方法总结:此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.三、板书设计一次函数的应用单个一次函数图象的应用一次函数与一元一次方程的关系探究的过程由浅入深,并利用了丰富的实际情景,增加了学生的学习兴趣.教学中要注意层层递进,逐步让学生掌握求一次函数与一元一次方程的关系.教学中还应注意尊重学生的个体差异,使每个学生都学有所获.

北师大初中数学八年级上册两个一次函数图象的应用1教案
解:∵y=23x+a与y=-12x+b的图象都过点A(-4,0),∴32×(-4)+a=0,-12×(-4)+b=0.∴a=6,b=-2.∴两个一次函数分别是y=32x+6和y=-12x-2.y=32x+6与y轴交于点B,则y=32×0+6=6,∴B(0,6);y=-12x-2与y轴交于点C,则y=-2,∴C(0,-2).如图所示,S△ABC=12BC·AO=12×4×(6+2)=16.方法总结:解此类题要先求得顶点的坐标,即两个一次函数的交点和它们分别与x轴、y轴交点的坐标.三、板书设计两个一次函数的应用实际生活中的问题几何问题进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题,在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维.在解决实际问题的过程中,进一步发展学生的分析问题、解决问题的能力和数学应用意识.

北师大初中数学八年级上册两个一次函数图象的应用2教案
学习目标1.掌握两个一次函数图像的应用;(重点)2.能利用函数图象解决实际问题。(难点)教学过程一、情景导入在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示.请你根据图象所提供的信息回答下列问题:甲、乙两根蜡烛燃烧前的高度分别是 厘米、 厘米,从点燃到燃尽所用的时间分别是 小时、 小时.你会解答上面的问题吗?学完本解知识,相信你能很快得出答案。二、 合作探究探究点一:两个一次函数的应用(2015?日照模拟)自来水公司有甲、乙两个蓄水池,现将甲池的中水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如下所示,结合图象回答下列问题.(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数表达式;(2)求注入多长时间甲、乙两个蓄水池水的深度相同;(3)求注入多长时间甲、乙两个蓄水的池蓄水量相同;

北师大初中数学八年级上册确定一次函数的表达式1教案
解:设正比例函数的表达式为y1=k1x,一次函数的表达式为y2=k2x+b.∵点A(4,3)是它们的交点,∴代入上述表达式中,得3=4k1,3=4k2+b.∴k1=34,即正比例函数的表达式为y=34x.∵OA=32+42=5,且OA=2OB,∴OB=52.∵点B在y轴的负半轴上,∴B点的坐标为(0,-52).又∵点B在一次函数y2=k2x+b的图象上,∴-52=b,代入3=4k2+b中,得k2=118.∴一次函数的表达式为y2=118x-52.方法总结:根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.【类型三】 根据实际问题确定一次函数的表达式某商店售货时,在进价的基础上加一定利润,其数量x与售价y的关系如下表所示,请你根据表中所提供的信息,列出售价y(元)与数量x(千克)的函数关系式,并求出当数量是2.5千克时的售价.

北师大初中数学八年级上册确定一次函数的表达式2教案
四个不同类型的问题由浅入深,学生能从不同角度掌握求一次函数的方法.对于问题4,教师可引导学生分析,并教学生要学会画图,利用图象分析问题,体会数形结合方法的重要性.学生若出现解题格式不规范的情况,教师应纠正并给予示范,训练学生规范答题的习惯.第五环节课时小结内容:总结本课知识与方法1.本节课主要学习了怎样确定一次函数的表达式,在确定一次函数的表达式时可以用待定系数法,即先设出解析式,再根据题目条件(根据图象、表格或具体问题)求出 , 的值,从而确定函数解析式。其步骤如下:(1)设函数表达式;(2)根据已知条件列出有关k,b的方程;(3)解方程,求k,b;4.把k,b代回表达式中,写出表达式.2.本节课用到的主要的数学思想方法:数形结合、方程的思想.目的:引导学生小结本课的知识及数学方法,使知识系统化.第六环节作业布置习题4.5:1,2,3,4目的:进一步巩固当天所学知识。教师也可根据学生情况适当增减,但难度不应过大.

