-

幼儿园中班教案说课稿 搬新家
在“我爱我家”主题开展过程中,我们为幼儿创设了一种家的氛围,让幼儿产生爱的体验。我想,音乐活动也可以配合这一主题,丰富幼儿的情感。因此,我就想以大头儿子和小头爸爸这两个幼儿耳熟能详的动画人物为主人公,创设一个活动情景作为本次活动的载体。一方面,活动中的律动动作大部分是双人动作,如亲一亲、抱一抱、压跷跷板等,既能在日常生活中幼儿与父母身上找到痕迹,又能体现亲子感情,所以用大头儿子和小头爸爸贯穿整个活动,可以自然地激发幼儿对家人、对亲情的认知和体验。

幼儿园大班主题说课稿 鸟的家族
“鸟”是动物世界中的一个大的家族。在厦门,到处都可以看到鸟的身影、听到鸟的叫声。而且教育的资源也很丰富:家庭养鸟、花鸟市场、公园,厦门的白鹭洲有鸽子,鼓浪屿上有“百鸟园”等。大班的孩子对鸟的认识有一定的经验,他们喜欢给鸟喂食,还喜欢亲近鸟。这些鸟有着不同的外表,不同的生活习性,不同的生活环境,对人类有不同的作用。那么多的鸟也有相同的特征:有羽毛,有翅膀、会飞……。新《纲要》告诉我们,“要与社区密切合作、综合利用各种教育资源,共同为幼儿的发展创造良好的条件。”因此,我认为,引导幼儿进一步探索鸟与人类的关系,探索不同鸟类的不同的生活环境有着一定的教育价值。 2.目标定位:活动目标是教育活动的起点和归宿,对活动起着导向的作用。依据大班幼儿的年龄特点和教材本身的特点,我从情感态度、能力、认知等方面确定了本次活动的目标,其中既有独立表达的成分,又有相互融和的一面。

幼儿园大班社会教案:百家姓
活动准备: 1、事先请幼儿向家长了解自己的名字的写法、含义和取名字的小故事。 2、写有幼儿名字的海报,贴在黑板上。 活动过程: 一、出示写有幼儿名字的海报导入 1、教师:你能找到自己的名字在哪里吗? 2、幼儿到海报上找出自己的名字。并学习用“这是我的名字,我叫ⅹⅹⅹ”的句式表达。 3、教师:我们的名字都一样吗? 4、教师小结:我们每个人都有一个名字,每个人的名字都不一样,有的名字有两个字,有的名字有三个字,还有一部分是四个字的。

幼儿园中班安全教案:小鸭找家
二、 活动准备:1、故事挂图、故事磁带、动物头饰、警察服装。2、课前让幼儿知道自己妈妈的名字。 三、活动过程:1、听看结合,欣赏故事:1)、邀请教师带上动物头饰给小朋友表演故事《小鸭找家》。再请小朋友说一说:——“故事中的小鸭怎么了?”——“谁来帮助它?最后小鸭子找到妈妈了吗?”教师小结:小鸭迷路找不到家了,小兔子、小猪、小鸟来帮助它,最后小鸭子找到妈妈了。

幼儿园中班美术教案:蜗牛的家
2、能大胆作画,并能丰富画面。活动准备 蜗牛范画、绘画纸、蜡笔 活动过程 1、出示蜗牛,引起幼儿兴趣 教师提问:这是什么?蜗牛的身子是什么样子的? 引导幼儿观察蜗牛壳的外形特征。 2、书空练习,帮助幼儿理解“螺旋线”。 教师边讲边做动作:蜗牛小时候也很小的,后来它一点一点长大,背上的壳也一圈一圈越长越大,后来就长成了一只大蜗牛。 教师:你们说蜗牛的身子是怎样长大的呢? 引导幼儿做书空练习。

幼儿园中班体育教案:小免搬家
2、激发对体育活动的兴趣,充分体验游戏的快乐。活动准备: 可乐瓶若干,塑料圈人手一个,斜坡一个,杂物若干,录音机,磁带。活动过程:1、准备运动:兔子舞 师戴头饰:孩子们,我们一起来跳个舞吧!(音乐起) 2、基本动作:游戏《狼来了》 师:这儿真美,我们在这儿安家吧!(取下圈,放在地上当家)我们还有很多粮食没搬,得把它们搬到仓库里。(指定一个地点为仓库)示范:走到场地一侧,取一件物品,用双腿夹住,跳到仓库处放下,再继续。(请个别幼儿示范,强调动作要领:在搬时一定要用夹物跳的方法。)当大灰狼出现时,小兔要立即在塑料圈中蹲下,大灰狼走了,再继续搬东西。 幼儿在音乐伴奏下练习两次。

别墅私家花园绿化养护协议
经甲乙双方平等协商,就甲方位于 私家花园别墅绿化委托乙方养护,达成如下协议: 一、养护项目内容 养护范围:主体楼周围栅栏之内,庭院绿植。(不包括盆景、室内盆栽及自行种植的两年成活年期内的树木)二、养护期限 养护期限自 年 月 日至 年 月 日截止。 三、养护职责 1、养护期限内,乙方应按照绿化养护操作规程及绿化养护质量标准,合理组织,精心养护,保质保量完成养护管理任务。 2、绿化设施及主要养护内容 修剪:根据各类植物的生长特点、立地环境、景观要求,按照操作规程适时进行。 施肥:根据各类植物的生长特点及植物对肥料的需要,要求年施肥不得少于2次以上,新种植物视生长情况,适时适量进行施肥,以保持各类植物的生长旺盛达到一定景观效果。 抹芽:主要用于乔木、大型灌木,对不定芽要及时清除,以保持树木骨架清晰,促使生长形态美观,营养集中。 病虫害防治:病虫害防治是植物养护中较为重要的手段和内容,要根据各类植物的寄生对象及时做好预测预报,及时采取措施防治。

别墅私家花园绿化养护协议
经甲乙双方平等协商,就甲方位于 私家花园别墅绿化委托乙方养护,达成如下协议: 一、养护项目内容 养护范围:主体楼周围栅栏之内,庭院绿植。(不包括盆景、室内盆栽及自行种植的两年成活年期内的树木)二、养护期限 养护期限自 年 月 日至 年 月 日截止。 三、养护职责 1、养护期限内,乙方应按照绿化养护操作规程及绿化养护质量标准,合理组织,精心养护,保质保量完成养护管理任务。 2、绿化设施及主要养护内容 修剪:根据各类植物的生长特点、立地环境、景观要求,按照操作规程适时进行。 施肥:根据各类植物的生长特点及植物对肥料的需要,要求年施肥不得少于2次以上,新种植物视生长情况,适时适量进行施肥,以保持各类植物的生长旺盛达到一定景观效果。 抹芽:主要用于乔木、大型灌木,对不定芽要及时清除,以保持树木骨架清晰,促使生长形态美观,营养集中。 病虫害防治:病虫害防治是植物养护中较为重要的手段和内容,要根据各类植物的寄生对象及时做好预测预报,及时采取措施防治。 抗旱、抗台、抗涝:旱季及新种植物要及时进行灌溉,防止植物因脱水而造成枯死。雨汛期间要做好加固、排涝抢险工作,防止植物受损。

学习《未成年人保护法》个人心得体会范文精选
一是要提高教育者的法律意识,使教育者自觉遵守法律规定。了解法律并遵守法律,应落实到每一位教师在日常教学的具体行动中。 二是要了解并尊重未成年人的客观需要,不以教师的主观意愿去要求孩子。未成年人正处在生长发育的过程中,有其自身的需要和特点。比如孩子好动,不可能像成年人那样长时间安静地坐着不动。因此,教师应充分认识和理解未成年人发展的客观规律,不能凭者自己的主观意愿去看待孩子、要求孩子。

学生学习《未成年人保护法》心得体会参考范文
孩子们是国家的未来祖国的希望,我们对他们的合法权给予特殊呵护,也是一项具有挑站性的工作,这需要全社会共同参与到其中,我们每一个人一起完成,共同维护未成年人合法权益,更好的履行自己的责任和义务,让孩子们活泼健康快乐的成长,成为一代强人,将来为祖国做出更大的贡献。

学生学习《未成年人保护法》心得体会参考范文
孩子们是国家的未来祖国的希望,我们对他们的合法权给予特殊呵护,也是一项具有挑站性的工作,这需要全社会共同参与到其中,我们每一个人一起完成,共同维护未成年人合法权益,更好的履行自己的责任和义务,让孩子们活泼健康快乐的成长,成为一代强人,将来为祖国做出更大的贡献。

湖南省张家界市2015年中考语文真题试题(含答案)
①马铃薯是菜还是粮?在1月6日举办的马铃薯主粮化发展战略研讨会上,丰富多彩的马铃薯主食制品令人大开眼界。马铃薯全粉占比40%的馒头、面包、马铃薯芝士蛋糕等,都颠覆着人们对马铃薯的认知。②农业部副部长在会上表示,要以科技创新引领马铃薯主粮化发展,推动形成马铃薯与谷物协调发展的新格局。据介绍,马铃薯有望成为稻米、小麦、玉米之外的第四大主粮作物。它的种植面积将逐步扩大到1.5亿亩,年产鲜薯增加2亿吨,折合粮食约为5000万吨。

湖南省张家界市2019年中考语文真题试题(含解析)
读书不能死章句,需要思考一个“活”字。李白在《嘲鲁儒》中说:“鲁叟谈五经,白发死章句。问以经济策,茫如坠烟雾。”诗人对那些夸夸其谈而没有真才实学的“鲁叟”进行了辛辣的嘲讽。这些人谈起五经头头是道,问起经世济民之策却茫然无知。他们拿腔拿调,架子十足,却死于章句,不知时变。陆游《冬夜读书示子聿》中的观点,则更加值得那些“鲁叟”们深思。他说“纸上得来终觉浅,绝知此事要躬行”,言词朴素,满含哲理,诗中提出的理论与实践相结合的观点,至今犹有现实意义。只有在实践中才能得真知、悟真谛,真正学有所获,学有所用。
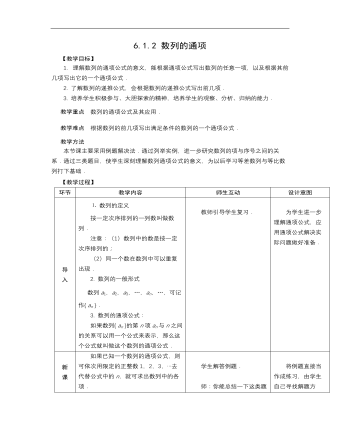
高教版中职数学基础模块下册:6.1《数列的概念》教案设计
【教学目标】1. 理解数列的通项公式的意义,能根据通项公式写出数列的任意一项,以及根据其前几项写出它的一个通项公式.2. 了解数列的递推公式,会根据数列的递推公式写出前几项.3.培养学生积极参与、大胆探索的精神,培养学生的观察、分析、归纳的能力.教学重点 数列的通项公式及其应用.教学难点 根据数列的前几项写出满足条件的数列的一个通项公式.教学方法 本节课主要采用例题解决法.通过列举实例,进一步研究数列的项与序号之间的关系.通过三类题目,使学生深刻理解数列通项公式的意义,为以后学习等差数列与等比数列打下基础.【教学过程】 环节教学内容师生互动设计意图导 入⒈数列的定义 按一定次序排列的一列数叫做数列. 注意:(1)数列中的数是按一定次序排列的; (2)同一个数在数列中可以重复出现. 2. 数列的一般形式 数列a1,a2,a3,…,an,…,可记作{ an }. 3. 数列的通项公式: 如果数列{ an }的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 教师引导学生复习. 为学生进一步理解通项公式,应用通项公式解决实际问题做好准备.

高教版中职数学基础模块下册:6.3《等比数列》优秀教案设计
授课 日期 班级16高造价 课题: §6.3等比数列 教学目的要求: 1.理解等比数列的概念,能根据定义判断或证明一个数列是等比数列;2.探索并掌握等比数列的通项公式; 3.掌握等比数列前 n 项和公式及推导过程,能用公式求相关参数; 教学重点、难点:运用等比数列的通项公式求相关参数 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》 授课执行情况及分析: 板书设计或授课提纲 §6.3等比数列 1.等比数列的概念 (学生板书区) 2. 等比数列的通项公式 3.等比数列的求和公式

高教版中职数学基础模块下册:8.3《两条直线的位置关系》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 8.3 两条直线的位置关系(二) *创设情境 兴趣导入 【问题】 平面内两条既不重合又不平行的直线肯定相交.如何求交点的坐标呢? 图8-12 介绍 质疑 引导 分析 了解 思考 启发 学生思考 *动脑思考 探索新知 如图8-12所示,两条相交直线的交点,既在上,又在上.所以的坐标是两条直线的方程的公共解.因此解两条直线的方程所组成的方程组,就可以得到两条直线交点的坐标. 观察图8-13,直线、相交于点P,如果不研究终边相同的角,共形成四个正角,分别为、、、,其中与,与为对顶角,而且. 图8-13 我们把两条直线相交所成的最小正角叫做这两条直线的夹角,记作. 规定,当两条直线平行或重合时,两条直线的夹角为零角,因此,两条直线夹角的取值范围为. 显然,在图8-13中,(或)是直线、的夹角,即. 当直线与直线的夹角为直角时称直线与直线垂直,记做.观察图8-14,显然,平行于轴的直线与平行于轴的直线垂直,即斜率为零的直线与斜率不存在的直线垂直. 图8-14 讲解 说明 讲解 说明 引领 分析 仔细 分析 讲解 关键 词语 思考 思考 理解 思考 理解 记忆 带领 学生 分析 带领 学生 分析 引导 式启 发学 生得 出结 果

空间向量基本定理教学设计人教A版高中数学选择性必修第一册
反思感悟用基底表示空间向量的解题策略1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.例2.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG=1/3 CD(1)证明:EF⊥B1C;(2)求EF与C1G所成角的余弦值.思路分析选择一个空间基底,将(EF) ?,(B_1 C) ?,(C_1 G) ?用基向量表示.(1)证明(EF) ?·(B_1 C) ?=0即可;(2)求(EF) ?与(C_1 G) ?夹角的余弦值即可.(1)证明:设(DA) ?=i,(DC) ?=j,(DD_1 ) ?=k,则{i,j,k}构成空间的一个正交基底.

点到直线的距离公式教学设计人教A版高中数学选择性必修第一册
4.已知△ABC三个顶点坐标A(-1,3),B(-3,0),C(1,2),求△ABC的面积S.【解析】由直线方程的两点式得直线BC的方程为 = ,即x-2y+3=0,由两点间距离公式得|BC|= ,点A到BC的距离为d,即为BC边上的高,d= ,所以S= |BC|·d= ×2 × =4,即△ABC的面积为4.5.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.解:(方法一)∵点A(1,1)与B(-3,1)到y轴的距离不相等,∴直线l的斜率存在,设为k.又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.由点A(1,1)与B(-3,1)到直线l的距离相等,∴直线l的方程是y=2或x-y+2=0.得("|" k"-" 1+2"|" )/√(k^2+1)=("|-" 3k"-" 1+2"|" )/√(k^2+1),解得k=0或k=1.(方法二)当直线l过线段AB的中点时,A,B两点到直线l的距离相等.∵AB的中点是(-1,1),又直线l过点P(0,2),∴直线l的方程是x-y+2=0.当直线l∥AB时,A,B两点到直线l的距离相等.∵直线AB的斜率为0,∴直线l的斜率为0,∴直线l的方程为y=2.综上所述,满足条件的直线l的方程是x-y+2=0或y=2.

两点间的距离公式教学设计人教A版高中数学选择性必修第一册
一、情境导学在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小?二、探究新知问题1.在数轴上已知两点A、B,如何求A、B两点间的距离?提示:|AB|=|xA-xB|.问题2:在平面直角坐标系中能否利用数轴上两点间的距离求出任意两点间距离?探究.当x1≠x2,y1≠y2时,|P1P2|=?请简单说明理由.提示:可以,构造直角三角形利用勾股定理求解.答案:如图,在Rt △P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,所以|P1P2|=?x2-x1?2+?y2-y1?2.即两点P1(x1,y1),P2(x2,y2)间的距离|P1P2|=?x2-x1?2+?y2-y1?2.你还能用其它方法证明这个公式吗?2.两点间距离公式的理解(1)此公式与两点的先后顺序无关,也就是说公式也可写成|P1P2|=?x2-x1?2+?y2-y1?2.(2)当直线P1P2平行于x轴时,|P1P2|=|x2-x1|.当直线P1P2平行于y轴时,|P1P2|=|y2-y1|.

两条平行线间的距离教学设计人教A版高中数学选择性必修第一册
一、情境导学前面我们已经得到了两点间的距离公式,点到直线的距离公式,关于平面上的距离问题,两条直线间的距离也是值得研究的。思考1:立定跳远测量的什么距离?A.两平行线的距离 B.点到直线的距离 C. 点到点的距离二、探究新知思考2:已知两条平行直线l_1,l_2的方程,如何求l_1 〖与l〗_2间的距离?根据两条平行直线间距离的含义,在直线l_1上取任一点P(x_0,y_0 ),,点P(x_0,y_0 )到直线l_2的距离就是直线l_1与直线l_2间的距离,这样求两条平行线间的距离就转化为求点到直线的距离。两条平行直线间的距离1. 定义:夹在两平行线间的__________的长.公垂线段2. 图示: 3. 求法:转化为点到直线的距离.1.原点到直线x+2y-5=0的距离是( )A.2 B.3 C.2 D.5D [d=|-5|12+22=5.选D.]

