-

助理工作计划
1.市场力度不够强,以至于现在唐山大企业中好多客户都还没接触过,没有合同产生!没有达到预期效果! 2.个人做事风格不够勤奋.不能做到坚持到最后,特别是最近今年四至八月份,拜访量特别不理想! 3.在工作和生活中,与人沟通时,说话的方式、方法有待进一步改进。

学校工会委员会工作制度
二、认真贯彻执行学校教职工代表大会的决议及上级工会的决定,负责主持学校工会的日常工作。 三、制定学校工会的各项工作计划,各种会议的组织实施及各类学习的安排,并做到有布置、有检查、有落实、有总结。 四、围绕学校教育教学、建设,组织教职工开展劳动竞赛、合理化建议、教育改革和教育创新活动。

XX区城市管理2024年上半年XX区城市管理工作总结
三是补齐市政设施建设短板。按照“花小钱、办实事”的原则,开展“城市体检”,排查城市污水、排水井116个,更换污水井盖27个、排水井12个;排查城市路灯1470个,更换维修310个;对城区21座桥梁进行安全排查,整改安全隐患4处;维护主次干道46处计5.11公里,维修人行道青石板453平方,更换城区损坏破损的座椅55把,疏通雨水管道216米,整治“空中管线”55处。五、重长效强监管,城市安全管理实现新突破一是大力开展油烟污染治理。对城区79家机关企事业单位,127家餐饮企业及城区工地食堂开展油烟污染全面排查检测1次,下发整改通知25份。实施规范管理,定期开展执法检查,要求“三个灶台”及以上必须安装油烟净化器,并聘请专业清洗公司对油烟净化器定期进行清洗,建立清洗台账,做好台账式管理,目前城区油烟净化装置安装使用率95%以上,达标排放率90%以上。

2023年第三季度工作总结和第四季度计划汇编(4篇)
(五)持续强化林产培育。2023年,全州林业总产值目标任务xxx亿元,前三季度完成林业总产值xxx.xx亿元,完成率xx%;全州录入投促系统的林业招商引资到位资金x.xx亿元。一是特色林业稳步发展。2023年,全州特色林业产业基地建设面积任务x.xx万亩,产量任务为x.xx万吨,产值任务为xx.xx亿元。前三季度完成特色林业基地建设面积x.xx万亩,产量x.xx万吨,产值为xx.xx亿元,面积年度目标任务完成率xx.xx%,产量年度目标任务完成率xx.xx%,产值年度目标任务完成率xx.xx%,预计到年度特色林业基地建设面积、产量、产值均能完成年度目标任务。二是林下经济初具规模。2023年,省下达我州利用林地发展林下经济面积达到xxx万亩、产值达到xx亿元。前三季度全州累计经营和利用林地发展林下经济面积xxx.xx万亩,产值xx.xx亿元,面积年度目标任务完成率xxx.xx%,产值年度目标任务完成率xx.xx%,预计到年底全州经营和林下经济利用面积、产值均能完成年度目标任务。

物业管理年度总结范本参考
从20**年11月到Xx市一中物业管理处以来,在管理处领导的关心和支持下,我努力适应新的工作环境和工作岗位,及时转变工作角色,努力学习业务管理知识,认真履行职责,较好地完成了学校和管理处交办的各项工作任务,下面将20**年的工作情况总结如下: 一、自觉加强学习,努力适应工作 20**年11月因公司工作安排,将我从x卫校管理处调到一中管理处工作,并担任勤杂班班长。在这之前我对班长的职责任务不甚了解,为了尽快适应新的工作岗位和工作环境,我自觉加强学习,虚心求教释惑,不断理清工作思路,总结工作方法,现已基本胜任本职。一方面,干中学、学中干,不断掌握方法积累经验。我注重以工作任务为牵引,依托工作岗位学习提高,通过观察、摸索、查阅资料和实践锻炼,较快地进入了工作情况。另一方面,问书本、问同事,不断丰富知识掌握技巧。在各级领导和同事的帮助指导下,从不会到会,从不熟悉到熟悉,我逐渐摸清了工作中的基本情况,找到了切入点,把握住了工作重点和难点。 二、心系本职工作,认真履行职责 作为管理处的勤杂班班长,首先就要求我要带好头,领好路。在工作中,不打任何折扣的去完成公司和学校领导交办的各项工作任务。今年以来,勤杂班克服各种困难顺利完成了学校110周年校庆、第十五届教育教学科技成果展、20**年中高考、人大代表选举等重大活动的后勤保障任务,完成了3500多件日常设施设备报修工作,班组成员不辞辛劳的工作,受到公司和学校领导的高度肯定。在管理上,要求班组成员之间做好互帮互助,工作不分你我,严格执行公司和学校的相关管理制度。

非全日制用工劳动合同
第四条乙方同意根据甲方工作需要,担任的以下工作:第五条乙方的工作时间;第六条乙方完成本合同约定的工作内容后,甲方应当以货币形式向乙方支付劳动报酬,劳动报酬标准为每小时_________元。甲方向乙方支付劳动报酬的周期不得超过15日。支付劳动报酬的其他约定。

幼儿园年度月度工作计划
1)抓常规教学。常规是基础,努力从备课、上课、听课、评课、作业批改、单元测试、综合测试和课后辅导等方面来抓,最终从阶段检测来督促和整改。 (2)积极贯彻新的教学理念,发挥学生的积极性、主动性和创造性,抓好课堂教学的有效性。 (3)开展不同形式的学科竞赛来促进和激发学生的潜力,培优从基础做起。 (4)抓好考试管理,从两个方面入手:监考和学生作弊。

小学各项规章制度大全通用
二、教研活动时间原则上每月一次。各教研组长应根据本组实际自行确定时间,召集本组全体成员参加,任何人不得无故请假或迟到早退。 三、教研组内开展教研活动,必须邀请学校一名中层以上干部参加活动,第次活动必须作好记录,并由参加活动的领导签字。各教研组长必须于每月底将教研记载情况交教导室检查评估,未经领导签字的记载一律无效。

销售主管的工作计划3篇
1、根据上一阶段的工作,找到当前工作流程中的漏洞,比如是否有本部门无法解决的问题,是否有需要相关部门协助解决而没有具体的人和方法来落实的问题; 2、所有本楼层的员工是否清楚本岗位的工作职责及相应的工作流程,是否有能力做好本职工作及所在岗位需要帮助解决的问题,是否按照相应的要求来做好本职工作; 3、了解本楼层专柜经营中需要解决的问题,例如灯光照明、商品陈列、库存积压等等。

食品安全监管工作计划
1.全园教职工要把幼儿安全问题置于头等重要地位,加强对工作的责任感,强化安全意识,认真细致地做好工作,避免意外事故的发生。 2.在每周的园务会议上,提醒各教职工重视卫生保健工作,加强对幼儿的安全保护工作。 三、重环境安全,避免事故发生 1.经常检查防火设施,注意易燃物品存放的安全及电源电闸的安全;后勤人员每月中、月底进行一次安全检查更换,确保有效使用。 2.后勤人员每周一检查大型玩具设施,发现有损坏脱落及被锈蚀及时处理。

仓库主管工作计划书
1)发扬吃苦耐劳精神。面对仓库中事务杂、任务重的工作性质,不怕吃苦,主动找事干,做到“眼勤、嘴勤、手勤、腿勤”,积极适应各种环境,在繁重的工作中磨练意志,增长才干。2) 发扬虚心学习精神。加强学习,勇于实践,博览群书,在向书本学习的同时注意收集各类信息,广泛吸取各种“营养”;同时,讲究学习方法,端正学习态度,提高 学习效率,努力培养自己具有扎实的工作基础、辩证的思维方法、正确的思想观点。力求把工作做得更好,树立本部门良好形象。

2022学校后勤主管工作计划
二、提高后勤队伍素质。为了提高后勤队伍素质,本学期按排了厨师上岗培训,更好地为幼儿服务,另外,为了使幼儿能安全地在幼儿园,门卫还将配备保安。除此之外,各部门还将定期组织人员进行业务培训,尽潜力抓好后勤人员的思想和业务工作,不断改善服务质量。三、重视安全教育工作。为进一步做好安全教育工作,加强《宁波市中小学生安全条例》管理,切实加强对安全教育工作的领导,本园将把各项安全工作列入重点议事日程,让幼儿不断增加安全意识。另外,还将完善幼儿园管理系统,使家园联系更方便。幼儿园每一天还务必做好常规安全工作检查,以便能及时整改。

宿管半年工作计划范文
一、围绕中心,服从大局,做好宿舍调整及管理服务工作 1、做好宿舍调整工作。为了达到学校提出的有关住宿标准,宿舍管理方面,克服各种困难;积极做好学生的思想工作,有力确保了学校的安全稳定大局。 2、宿舍晚间熄灯制度。为了配合校风学风建设,加强对学生管理制度,熄灯后加强了查宿舍人员名单,了解学生动态情况。有什么问题及时上报。

2023年法治建设工作总结和2024年工作计划汇编(6篇)
四是严格落实公平竞争审查制度。建立健全公平竞争审查机制,印发了《xx经济和信息化局公平竞争审查制度实施方案(试行)》,进一步明确了各科室审查责任和审查内容,坚决不允许出现影响企业公平竞争的限制性措施。今年,共审查规范性文件x件,均未出现影响公平竞争的相关措施。加强对妨碍统一市场、不正当竞争等问题整治,全面落实市场准入负面清单制度。五是持续提升监管效能。全面推行监管执法“一目录,五清单”制度,积极配合州交通局开展“双随机一公开”工作,加强机动车违规改装的监管工作。(三)健全体系,全面推进政府治理规范化程序化法治化一是加强规范性文件清理。全面落实规范性文件合法性审查制度,制定单位规范性文件备案审查程序,未经合法性审查或审查不合法的,不予审议印发。及时制定《州经信局关于开展州政府规章、行政规范性文件清理工作方案》,明确了清理范围、清理标准、方法和责任主体,全面清理了20xx年x月x日至2022年xx月xx日以x府发、x府函、x府办发、x府办函、x府规、x府办规等x种字号印发的州政府文件,共清理非涉密文件xx件,经合法性审核、集体审议,建议废止x件、失效xx件、拟修改x件,继续有效xx件。

工程建设招标设标合同合同条件
除非合同另有规定,承包人应全权负责无论地方的还是其他方面的劳务及职员的雇用,工资的支付、房屋、膳食及运输的安排。承包人不应从为业主或监理工程师服务的人员中招募劳务或职员,承包人应负责将为履行合同而招募的人员送回原籍,并安排将要送回但尚未返回人员的生活,直到他们离开工地。非中国籍的及在国外招募的人员应在施工完成后离开中国。34.2承包商的外警劳务及职员除自有劳务来源及接第16.2款和34.3款规定办理之外,承包人应按下述(a)至(d)款的详细规定,负责本工程所需的外籍劳力和外籍职员(下称“外籍人员”)招募、交通和食市供应以及与此有关的人员费用支付。。(a)承包人所在外籍人员及他们家庭成员的出入境签证、中转签证及居住许可证等的发放应遵守中国的有关规定。承包人应负责为进入中国境内的外籍人员获取所有必需的签证或许可证。

工程建设招标设标合同合同条件
承包人应在每月末应向监理工程师提交四份接监理工程师要求的格式报表,每份均由监理工程师按第15.1款规定的承包人代表签字,报表包括承包人认为到月底自己有权得到的以下有关各项的款额:(a)已实施的永久工程的价值;(b)工程量表中的任何其它项目,包括承包人的设备、临时工程、计日及类似项目;(c)表列材料及承包人在工地交付的用于永久工程的待安装设备发票价值的百分比,如投标书中附录中所注明的;(d)按第70款的调整;(e)按合同规定承包人有权得到的任何其它金额。如适应,月报表应包括如下项目并按其顺序考虑:(l)截止到本月末已实施完成永久工程以人民币计价的估计合同值,该值应据56款规定为工程量清单中书明的场本单价乘以由监理工程师测定的工程量。(2)按(1)中所述方法截止到上月末完成的永久性工程的估算合同值。(3)以当地货币表示的本月永久工程合同估算值,即上述(1)减掉(2)。(4)据表1所表明的外币百分比计算出(3项中当地货币和外币的数额根据52款规定,它是受变更影响的。

办公室工作的调研报告范文
一、解放思想、大胆创新 社会在发展,历史在进步,人保公司也处于前所未有的历史变革时期,办公室工作人员必须搭准历史发展的脉搏,跟上历史发展的脚步,合上历史发展的节律。为此,就要解放思想、转变观念、大胆创新。日常工作中要敢于打破旧框框,革除陈规陋习,面对新情况、新问题,要勇于思考,敢于探索,大胆地推进工作创新。如:公文运转如何做到急事急办、特事特办?如何改进接待工作,如何适应业务发展加大宣传工作力度等等。有了超前的意识、大胆创新精神和灵活多变的手段,就能使办公室工作有声有*、富有成效。

(3篇)2024年学校办公室工作总结汇报
生活赋予我们的不仅是忙碌和烦恼,还有成长的触动和顿悟。担任办公室主任一职,让我感受颇多,受益匪浅。由衷地感谢学校领导的信任,感谢大家对我工作的支持,特别是工作出现差错时给予的谅解与关爱。在今后工作中我将虚心接受大家批评和监督,不断进步。了这个永久的目标,办公室的脚步永不停留,我们的奋斗永无止息!让我们以烈火如佘的热情迎接下学期的工作吧。学校办公室工作总结汇报篇三首先非常感谢各位领导和同志们对办公室工作和我个人工作的支持。在本学期,虽然我正式承担其办公室的全面工作,但我在办公室已经整整工作四年了,对办公室的工作应该说很熟悉。我感到非常高兴的是办公室全体人员十分团结,对分配的任何工作都没有怨言,全体领导和老师对办公室的工作能够给与充分的理解。本学期,为了落实学校总体工作目标,全面贯彻学校“严、新、实、快”的工作作风,依托高立意、低起点、严要求的工作策略,稳步树立了有礼有节、不卑不亢的.

国旗下讲话(小学):爱护公物
尊敬的领导、老师,亲爱的同学们:大家早上好!今天,我演讲的题目是《爱护公物》。伴随着清晨冉冉升起的朝阳,同学们高高兴兴地来到学校,看着我们庄严的教学楼,宽敞的操场,还有那美丽的校园一角,你的心情是不是很舒畅呢?但是,当你出于一时的不快,用拳头砸碎消防窗的玻璃;当你出于一时的恶作剧,用笔尖划脏桌面时,你是否曾想过,那锋利的玻璃也会刺伤你的手;那上千张课桌将被损坏,这将会给蓬勃向上,给绿树环饶的校园抹上一笔刺眼的阴影。学校为了给我们营造一个优美的校园环境,花费了大量资金进行修建、改造。这一切都是为了让我们拥有一个既优美又舒适的学习环境,而我们个别同学却丝毫不懂得珍惜和爱护,有意或无意的就去损坏这些来之不易的公物,这是一种极不道德、不高尚的行为。
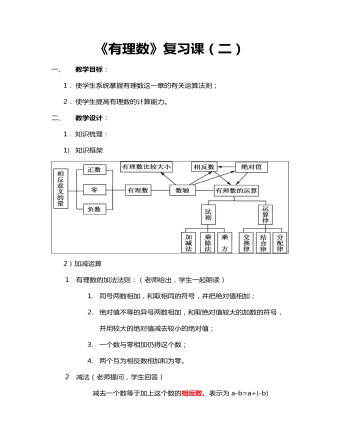
有理数复习教案教学设计
3)乘除运算①有理数的乘法法则:(老师给出,学生一起朗读)1. 两数相乘,同号得正,异号得负,并把绝对值相乘;2. 任何数与零相乘都得零;3. 几个不等于零的数相乘,积的符号由负因数的个数决定,当负因数有奇数个数,积为负;当负因数的个数为偶数个时,积为正;4. 几个有理数相乘,若其中有一个为零,积就为零。②有理数的除法法则:(老师提问,学生回答)1. 两个有理数相除,同号得正,异号得负,并把绝对值相除;2. 除以一个数等于乘以这个数的倒数。③关系(老师给出)除法转化为乘法进行运算。





















