-

关于法律的国旗下讲话
在我们的心中,应当始终有两盏高悬的明灯伴随我们的一生:一盏是信仰,一盏是法律。如果说信仰给我们指明了前进的方向,那么法律便是保障我们顺利前进的航标。周公制礼,韩非说法。“没有规矩,不成方圆”。在人类文明历史演义的长河中,大凡有成就的人,无不明礼诚信,奉公守法。鞠躬尽瘁的孔明挥泪斩马谡,他的心中装的是军法;铁面无私的包拯忍痛斩亲侄,他的心中装的是律法。“法”犹如一颗璀璨的明珠,在他们心中始终闪耀着神圣不可侵犯的光芒。在庄严的法庭上,“法”是那张高悬的明镜,一尘不染;在老百姓的心目中,“法”则是那公平正义的天平,不偏不倚。世界第一部成文法——《乌尔纳姆法典》,诞生于公元前21世纪末的乌尔第三王朝,这颗法律的种子经过几千年日月精华的滋养和云电光风的考验,它现在已经成长成为一颗枝繁叶茂的参天大树,法,现在已渗透到了当今社会的每一个角落,并与我们每一个人息息相关。

读宪法国旗下讲话稿
关于宪法的定义,Wheare追随Dicey,认为广义的宪法是确立和控制政府的规则的集合体,这里说的政府是大政府,而非单纯的行政。那么怎么写一份演讲稿呢?下面和小编一起来看看吧!读宪法国旗下讲话稿【1】 宪法是国家的根本大法。宪法规定了一个国家社会制度、国家制度、国家机关组织和活动的基本原则,规定了公民的基本权利和义务等重要内容。宪法具有最高的法律效力,是制定其他法律的依据。也许有同学会说,宪法好像与我们现实生活没有交集。其实不是的,根据宪法,国家有关部门制定出了具体的法律法规和各项规章制度,如升国旗时,《国旗法》对我们的行为作出了具体要求;《中小学生日常行为规范》对我们的学习和品德养成提出了要求;当我们走进社会,《未成年人保护法》和《预防未成年人犯罪法》为我们保驾护航;当我们在消费遇到问题时,可以依据《消费者权益保护法》维护自己的合法权益。总之,我们中学生生活的各个领域,都与法律相伴。天高任鸟飞,海阔凭鱼跃。我们常常用这句话来表达自己对自由的向往。对鱼儿和鸟儿的自由羡慕至极。但是我们忘了鱼儿离不开水,鸟儿离不开天空。所以不存在绝对的自由。洛克说:“法律的目的不是废除或限制自由,而是保护和扩大自由……哪里没有法律,哪里就没有自由。”

法制安全国旗下讲话稿
安全这个永恒的主题,今天我们再一次提起它,心里总是沉甸甸的。安全究竟是什么?安全就是爱护和保护人的生命不受损害。法制安全国旗下讲话稿要怎么准备?下面是小编整理的法制安全国旗下讲话稿,欢迎阅读!法制安全国旗下讲话稿 敬爱的老师、亲爱的同学们:大家好!今天我演讲的主题是《法制安全从我做起》。同学们,我们青少年是祖国的未来和希望,我们能否健康成长,关系到家庭的幸福,关系到国家和民族的兴衰成败。所以,遵守法制、保障安全应从每个青少年做起,从我做起。俗话说:“无规矩不成方圆”。许多青少年犯罪的事实告戒我们,每位中学生都应做到知法、懂法、守法,要做到警钟长鸣、严以 律已,要做到遵守国家法律法规、严守校规校纪。同学们,你们可曾相信,全国每年有近万中小学生因交通事故、食物中毒、溺水等原因非正常死亡,这些数字多么令人触目惊心。为了我们健康成长、家庭幸福,我们每位同学都要做到事事讲安全,处处讲安全,时时讲安全。

法制宣传国旗下讲话
老师们、同学们:大家早上好!同学们,知道今天是什么日子吗?( )对,每年的12月4日是全国法制宣传教育日,今年12月4日是全国第九个法制宣传教育日,所以,尽管今天不是星期一,但是,我们还是要庄严地举行升旗仪式,在鲜艳的五星红旗下,我们共同来拉开本次法制宣传教育日各项活动的序幕,今天我国旗下讲话的题目是“学法 知法 守法 护法 为你为我为大家”。同学们知道吗?国家确定每年12月4日为法制宣传教育活动日,意义重大,目的是要求大家在“12·4”前后集中开展学法、用法、守法、护法活动,从而不断提高每个公民的法律意识和法律素质。为什么要全民学法呢?俗话说:“没有规矩不成方圆”,无论做什么事都要有个规矩,否则就什么也做不成。而法律就是我们全社会每个人都要遵守的规矩。是的,我们每天的学习、生活都要遵守基本的规矩,各项法律法规规范着我们行为,如升国旗时,《国旗法》对我们的行为要求就有约束;在上课、学习方面,《小学生守则》和《小学生日常行为规范》就对我们有所要求;在回家过马路时,《道路交通法》就对我们的行为进行了规范;在扔废品和纸屑时,《环境保护-法》、《爱国卫生条例》、《小学生守则》等也都作了相应的规定

法制教育国旗下讲话稿
同学们:大家好!今天,很高兴能和同学们在一起共同进行一次法制学习。其实,有些法律知识我应该向你们学习的,为什么呢?前不久,我陪同市领导到校调研的时候,观看了同学们自己编写的法制小故事,很真实,很深刻。其中有一位同学编写的一个毛阿敏偷税漏税的故事,我深受启发,这不仅仅是一个故事,而是你们的内心深处法律意识的真实反映。在这里,我也给大家讲一个我亲眼目睹、令人深思的真人真事。事情发生在四小区的住宅楼,这天正是星期日,三位初中生在四楼的楼道窗前嬉戏,甲失手将乙推出窗外,重重地从高达20米的四楼摔了下来。当时乙的脸色铁青,血从鼻孔、耳孔直往外淌。后来,乙被市医院急救车救走。此时,我给同学们出二个思考题:①甲失手致伤乙,算不算违法?②如果甲违法,违反了什么法?结果应是:如果医疗签定部门确定为重伤,首先甲这种行为造成的后果违法,其次甲违反了《刑法》第四章侵犯公民人身权利,民主权利罪第二百三十五条:过失伤害他人致人重伤,处三年以下有期徒刑或拘役。

专项法律服务合同
甲方因 事宜,为维护自身的合法权益,特聘请乙方提供专项法律服务,并代为办理该项工作中的有关法律事务。现依据我国《合同法》、《律师法》等相关法律法规,经双方协商一致签定本合同,以资各方诚信履行。第一条 甲方委托乙方提供如下法律服务:第二条 乙方的义务1、乙方委派执业律师为甲方办理合同第一条所列服务事项;2、乙方律师应当勤勉、尽责,尽最大努力维护甲方的合法权益;3、乙方律师应当在取得甲方提供的文件资料后及时完成服务,并应甲方要求通报工作进展情况;4、乙方律师在本合同期内,对涉及甲方的对抗性案件,不得担任与甲方具有法律上利益冲突的另一方的法律顾问或者代理人;5、乙方律师对其获知的甲方个人隐私、商业秘密负有保密义务。 第三条 甲方的义务 1、甲方应当真实、完整、及时地向乙方提供与本次委托事项有关的各种情况、文件、资料;2、甲方应当为乙方律师办理服务事项提出明确、合法合理的要求;3、甲方应当按时、足额向乙方支付约定的律师费;

聘请法律顾问合同
(以下简称甲方)由于工作需要,根据《中华人民共和国律师暂行条例》的有关规定,聘请北京市京融律师事务所(以下简称乙方)律师 为法律顾问,双方设立以下条款,共同遵守履行:一、律师在甲方对内对外经济事务中积极发挥法律顾问作用,包括提供法律咨询,参与审查、修改、起草各种法律事务文书,参与经济合同的谈判和签定活动。二、律师在参与调解、仲裁、代理诉讼活动中维护甲方的合法权益。三、甲方聘请律师担任法律顾问应向乙方交付费用每年 元。四、若律师为甲方去外地工作时,差旅、食宿等费用由甲方负责。五、本合同自签字盖章之日起生效,有效期 年。

聘请法律顾问合同格式
(以下简称甲方)因工作需要根据《中华人民共和国律师暂行条例》的有关规定,聘请 (以下简称乙方)的律师为法律顾问,经双方协商订立下列协议,共同遵照履行。一、乙方委派律师 担任甲方的法律顾问,为甲方提供法律帮助,依法维护甲方的合法权益。甲方指定 为法律顾问的联系人。二、法律顾问工作范围:1.为甲方解答法律问题,必要时提供法律意见书。2.协助草拟、修改、审查合同和有关法律事务文书。3.接受甲方委托,参与经济合同谈判。4.接受甲方委托,担任代理人,参加诉讼、非诉讼、调解、仲裁活动。
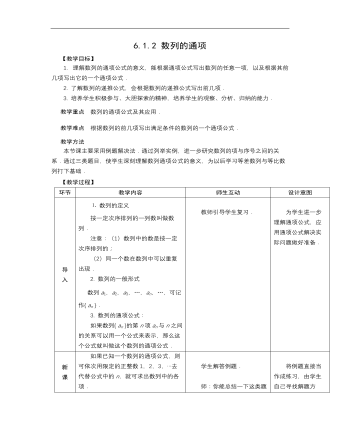
高教版中职数学基础模块下册:6.1《数列的概念》教案设计
【教学目标】1. 理解数列的通项公式的意义,能根据通项公式写出数列的任意一项,以及根据其前几项写出它的一个通项公式.2. 了解数列的递推公式,会根据数列的递推公式写出前几项.3.培养学生积极参与、大胆探索的精神,培养学生的观察、分析、归纳的能力.教学重点 数列的通项公式及其应用.教学难点 根据数列的前几项写出满足条件的数列的一个通项公式.教学方法 本节课主要采用例题解决法.通过列举实例,进一步研究数列的项与序号之间的关系.通过三类题目,使学生深刻理解数列通项公式的意义,为以后学习等差数列与等比数列打下基础.【教学过程】 环节教学内容师生互动设计意图导 入⒈数列的定义 按一定次序排列的一列数叫做数列. 注意:(1)数列中的数是按一定次序排列的; (2)同一个数在数列中可以重复出现. 2. 数列的一般形式 数列a1,a2,a3,…,an,…,可记作{ an }. 3. 数列的通项公式: 如果数列{ an }的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 教师引导学生复习. 为学生进一步理解通项公式,应用通项公式解决实际问题做好准备.

高教版中职数学基础模块下册:6.3《等比数列》优秀教案设计
授课 日期 班级16高造价 课题: §6.3等比数列 教学目的要求: 1.理解等比数列的概念,能根据定义判断或证明一个数列是等比数列;2.探索并掌握等比数列的通项公式; 3.掌握等比数列前 n 项和公式及推导过程,能用公式求相关参数; 教学重点、难点:运用等比数列的通项公式求相关参数 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》 授课执行情况及分析: 板书设计或授课提纲 §6.3等比数列 1.等比数列的概念 (学生板书区) 2. 等比数列的通项公式 3.等比数列的求和公式

高教版中职数学基础模块下册:8.3《两条直线的位置关系》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 8.3 两条直线的位置关系(二) *创设情境 兴趣导入 【问题】 平面内两条既不重合又不平行的直线肯定相交.如何求交点的坐标呢? 图8-12 介绍 质疑 引导 分析 了解 思考 启发 学生思考 *动脑思考 探索新知 如图8-12所示,两条相交直线的交点,既在上,又在上.所以的坐标是两条直线的方程的公共解.因此解两条直线的方程所组成的方程组,就可以得到两条直线交点的坐标. 观察图8-13,直线、相交于点P,如果不研究终边相同的角,共形成四个正角,分别为、、、,其中与,与为对顶角,而且. 图8-13 我们把两条直线相交所成的最小正角叫做这两条直线的夹角,记作. 规定,当两条直线平行或重合时,两条直线的夹角为零角,因此,两条直线夹角的取值范围为. 显然,在图8-13中,(或)是直线、的夹角,即. 当直线与直线的夹角为直角时称直线与直线垂直,记做.观察图8-14,显然,平行于轴的直线与平行于轴的直线垂直,即斜率为零的直线与斜率不存在的直线垂直. 图8-14 讲解 说明 讲解 说明 引领 分析 仔细 分析 讲解 关键 词语 思考 思考 理解 思考 理解 记忆 带领 学生 分析 带领 学生 分析 引导 式启 发学 生得 出结 果

空间向量基本定理教学设计人教A版高中数学选择性必修第一册
反思感悟用基底表示空间向量的解题策略1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.例2.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG=1/3 CD(1)证明:EF⊥B1C;(2)求EF与C1G所成角的余弦值.思路分析选择一个空间基底,将(EF) ?,(B_1 C) ?,(C_1 G) ?用基向量表示.(1)证明(EF) ?·(B_1 C) ?=0即可;(2)求(EF) ?与(C_1 G) ?夹角的余弦值即可.(1)证明:设(DA) ?=i,(DC) ?=j,(DD_1 ) ?=k,则{i,j,k}构成空间的一个正交基底.

点到直线的距离公式教学设计人教A版高中数学选择性必修第一册
4.已知△ABC三个顶点坐标A(-1,3),B(-3,0),C(1,2),求△ABC的面积S.【解析】由直线方程的两点式得直线BC的方程为 = ,即x-2y+3=0,由两点间距离公式得|BC|= ,点A到BC的距离为d,即为BC边上的高,d= ,所以S= |BC|·d= ×2 × =4,即△ABC的面积为4.5.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.解:(方法一)∵点A(1,1)与B(-3,1)到y轴的距离不相等,∴直线l的斜率存在,设为k.又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.由点A(1,1)与B(-3,1)到直线l的距离相等,∴直线l的方程是y=2或x-y+2=0.得("|" k"-" 1+2"|" )/√(k^2+1)=("|-" 3k"-" 1+2"|" )/√(k^2+1),解得k=0或k=1.(方法二)当直线l过线段AB的中点时,A,B两点到直线l的距离相等.∵AB的中点是(-1,1),又直线l过点P(0,2),∴直线l的方程是x-y+2=0.当直线l∥AB时,A,B两点到直线l的距离相等.∵直线AB的斜率为0,∴直线l的斜率为0,∴直线l的方程为y=2.综上所述,满足条件的直线l的方程是x-y+2=0或y=2.

两点间的距离公式教学设计人教A版高中数学选择性必修第一册
一、情境导学在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小?二、探究新知问题1.在数轴上已知两点A、B,如何求A、B两点间的距离?提示:|AB|=|xA-xB|.问题2:在平面直角坐标系中能否利用数轴上两点间的距离求出任意两点间距离?探究.当x1≠x2,y1≠y2时,|P1P2|=?请简单说明理由.提示:可以,构造直角三角形利用勾股定理求解.答案:如图,在Rt △P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,所以|P1P2|=?x2-x1?2+?y2-y1?2.即两点P1(x1,y1),P2(x2,y2)间的距离|P1P2|=?x2-x1?2+?y2-y1?2.你还能用其它方法证明这个公式吗?2.两点间距离公式的理解(1)此公式与两点的先后顺序无关,也就是说公式也可写成|P1P2|=?x2-x1?2+?y2-y1?2.(2)当直线P1P2平行于x轴时,|P1P2|=|x2-x1|.当直线P1P2平行于y轴时,|P1P2|=|y2-y1|.

两条平行线间的距离教学设计人教A版高中数学选择性必修第一册
一、情境导学前面我们已经得到了两点间的距离公式,点到直线的距离公式,关于平面上的距离问题,两条直线间的距离也是值得研究的。思考1:立定跳远测量的什么距离?A.两平行线的距离 B.点到直线的距离 C. 点到点的距离二、探究新知思考2:已知两条平行直线l_1,l_2的方程,如何求l_1 〖与l〗_2间的距离?根据两条平行直线间距离的含义,在直线l_1上取任一点P(x_0,y_0 ),,点P(x_0,y_0 )到直线l_2的距离就是直线l_1与直线l_2间的距离,这样求两条平行线间的距离就转化为求点到直线的距离。两条平行直线间的距离1. 定义:夹在两平行线间的__________的长.公垂线段2. 图示: 3. 求法:转化为点到直线的距离.1.原点到直线x+2y-5=0的距离是( )A.2 B.3 C.2 D.5D [d=|-5|12+22=5.选D.]

两直线的交点坐标教学设计人教A版高中数学选择性必修第一册
1.直线2x+y+8=0和直线x+y-1=0的交点坐标是( )A.(-9,-10) B.(-9,10) C.(9,10) D.(9,-10)解析:解方程组{■(2x+y+8=0"," @x+y"-" 1=0"," )┤得{■(x="-" 9"," @y=10"," )┤即交点坐标是(-9,10).答案:B 2.直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,则k的值为( )A.-24 B.24 C.6 D.± 6解析:∵直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,可设交点坐标为(a,0),∴{■(2a"-" k=0"," @a+12=0"," )┤解得{■(a="-" 12"," @k="-" 24"," )┤故选A.答案:A 3.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则点P的坐标为 . 解析:∵直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,且l1⊥l2,∴a×1+1×(a-2)=0,解得a=1,联立方程{■(x+y"-" 6=0"," @x"-" y=0"," )┤易得x=3,y=3,∴点P的坐标为(3,3).答案:(3,3) 4.求证:不论m为何值,直线(m-1)x+(2m-1)y=m-5都通过一定点. 证明:将原方程按m的降幂排列,整理得(x+2y-1)m-(x+y-5)=0,此式对于m的任意实数值都成立,根据恒等式的要求,m的一次项系数与常数项均等于零,故有{■(x+2y"-" 1=0"," @x+y"-" 5=0"," )┤解得{■(x=9"," @y="-" 4"." )┤

圆的标准方程教学设计人教A版高中数学选择性必修第一册
(1)几何法它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.(2)待定系数法由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:①设——设所求圆的方程为(x-a)2+(y-b)2=r2;②列——由已知条件,建立关于a,b,r的方程组;③解——解方程组,求出a,b,r;④代——将a,b,r代入所设方程,得所求圆的方程.跟踪训练1.已知△ABC的三个顶点坐标分别为A(0,5),B(1,-2),C(-3,-4),求该三角形的外接圆的方程.[解] 法一:设所求圆的标准方程为(x-a)2+(y-b)2=r2.因为A(0,5),B(1,-2),C(-3,-4)都在圆上,所以它们的坐标都满足圆的标准方程,于是有?0-a?2+?5-b?2=r2,?1-a?2+?-2-b?2=r2,?-3-a?2+?-4-b?2=r2.解得a=-3,b=1,r=5.故所求圆的标准方程是(x+3)2+(y-1)2=25.

圆的一般方程教学设计人教A版高中数学选择性必修第一册
情境导学前面我们已讨论了圆的标准方程为(x-a)2+(y-b)2=r2,现将其展开可得:x2+y2-2ax-2bx+a2+b2-r2=0.可见,任何一个圆的方程都可以变形x2+y2+Dx+Ey+F=0的形式.请大家思考一下,形如x2+y2+Dx+Ey+F=0的方程表示的曲线是不是圆?下面我们来探讨这一方面的问题.探究新知例如,对于方程x^2+y^2-2x-4y+6=0,对其进行配方,得〖(x-1)〗^2+(〖y-2)〗^2=-1,因为任意一点的坐标 (x,y) 都不满足这个方程,所以这个方程不表示任何图形,所以形如x2+y2+Dx+Ey+F=0的方程不一定能通过恒等变换为圆的标准方程,这表明形如x2+y2+Dx+Ey+F=0的方程不一定是圆的方程.一、圆的一般方程(1)当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0表示以(-D/2,-E/2)为圆心,1/2 √(D^2+E^2 "-" 4F)为半径的圆,将方程x2+y2+Dx+Ey+F=0,配方可得〖(x+D/2)〗^2+(〖y+E/2)〗^2=(D^2+E^2-4F)/4(2)当D2+E2-4F=0时,方程x2+y2+Dx+Ey+F=0,表示一个点(-D/2,-E/2)(3)当D2+E2-4F0);

直线的点斜式方程教学设计人教A版高中数学选择性必修第一册
【答案】B [由直线方程知直线斜率为3,令x=0可得在y轴上的截距为y=-3.故选B.]3.已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为________.【答案】y-1=-(x-2) [直线l2的斜率k2=1,故l1的斜率为-1,所以l1的点斜式方程为y-1=-(x-2).]4.已知两条直线y=ax-2和y=(2-a)x+1互相平行,则a=________. 【答案】1 [由题意得a=2-a,解得a=1.]5.无论k取何值,直线y-2=k(x+1)所过的定点是 . 【答案】(-1,2)6.直线l经过点P(3,4),它的倾斜角是直线y=3x+3的倾斜角的2倍,求直线l的点斜式方程.【答案】直线y=3x+3的斜率k=3,则其倾斜角α=60°,所以直线l的倾斜角为120°.以直线l的斜率为k′=tan 120°=-3.所以直线l的点斜式方程为y-4=-3(x-3).

直线的两点式方程教学设计人教A版高中数学选择性必修第一册
解析:①过原点时,直线方程为y=-34x.②直线不过原点时,可设其方程为xa+ya=1,∴4a+-3a=1,∴a=1.∴直线方程为x+y-1=0.所以这样的直线有2条,选B.答案:B4.若点P(3,m)在过点A(2,-1),B(-3,4)的直线上,则m= . 解析:由两点式方程得,过A,B两点的直线方程为(y"-(-" 1")" )/(4"-(-" 1")" )=(x"-" 2)/("-" 3"-" 2),即x+y-1=0.又点P(3,m)在直线AB上,所以3+m-1=0,得m=-2.答案:-2 5.直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 . 解析:直线在两坐标轴上的截距分别为1/a 与 1/b,所以直线与坐标轴围成的三角形面积为1/(2"|" ab"|" ).答案:1/(2"|" ab"|" )6.已知三角形的三个顶点A(0,4),B(-2,6),C(-8,0).(1)求三角形三边所在直线的方程;(2)求AC边上的垂直平分线的方程.解析(1)直线AB的方程为y-46-4=x-0-2-0,整理得x+y-4=0;直线BC的方程为y-06-0=x+8-2+8,整理得x-y+8=0;由截距式可知,直线AC的方程为x-8+y4=1,整理得x-2y+8=0.(2)线段AC的中点为D(-4,2),直线AC的斜率为12,则AC边上的垂直平分线的斜率为-2,所以AC边的垂直平分线的方程为y-2=-2(x+4),整理得2x+y+6=0.

