-
高教版中职数学基础模块下册:6.2《等差数列》教学设计
系(部)医药授课教师戚文撷授课班级11(5),11(6)班授课类型新授课授课时数2课时授课周数第一周授课日期2012.2.15授课地点 教室课题第六章数列分课题§6.2 等差数列教学目标1. 理解等差数列的概念,掌握等差数列的通项公式;掌握等差中项的概念. 2. 逐步灵活应用等差数列的概念和通项公式解决问题. 3.等差数列的前N项之和 . 4.培养学生分析、比较、归纳的逻辑思维能力. . 2. 3.教学重点等差数列的概念及其通项公式. 教学难点等差数列通项公式的灵活运用. 教学方法情境教学法、自主探究式教学方法教学器材及设备黑板、粉笔复习提问提问内容姓名成绩1.数列的定义? 答: 2. 数列的通项公式? 答: 板书设计 §6.2.1等差数列的概念 1. 1.等差数列的定义 公差:d 2.常数列 3.等差数列的通项公式 an=a1+(n-1)d. 等差数列的前n 项和公式: 例题 练习作业布置习题第1,2题.课后小结本节课主要采用自主探究式教学方法.充分利用现实情景,尽可能地增加教学过程的趣味性、实践性.我再整个教学中强调学生的主动参与,让学生自己去分析、探索,在探索过程中研究和领悟得出的结论,从而达到使学生既获得知识又发展智能的目的.

高教版中职数学基础模块下册:6.3《等比数列》优秀教案设计
授课 日期 班级16高造价 课题: §6.3等比数列 教学目的要求: 1.理解等比数列的概念,能根据定义判断或证明一个数列是等比数列;2.探索并掌握等比数列的通项公式; 3.掌握等比数列前 n 项和公式及推导过程,能用公式求相关参数; 教学重点、难点:运用等比数列的通项公式求相关参数 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》 授课执行情况及分析: 板书设计或授课提纲 §6.3等比数列 1.等比数列的概念 (学生板书区) 2. 等比数列的通项公式 3.等比数列的求和公式

【高教版】中职数学拓展模块:1.1《两角和与差的正弦公式与余弦公式》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.1两角和与差的余弦公式与正弦公式. *创设情境 兴趣导入 问题 我们知道,显然 由此可知 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 10*动脑思考 探索新知 在单位圆(如上图)中,设向量、与x轴正半轴的夹角分别为和,则点A的坐标为(),点B的坐标为(). 因此向量,向量,且,. 于是 ,又 , 所以 . (1) 又 (2) 利用诱导公式可以证明,(1)、(2)两式对任意角都成立(证明略).由此得到两角和与差的余弦公式 (1.1) (1.2) 公式(1.1)反映了的余弦函数与,的三角函数值之间的关系;公式(1.2)反映了的余弦函数与,的三角函数值之间的关系. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 启发引导学生发现解决问题的方法 25

高教版中职数学基础模块下册:8.3《两条直线的位置关系》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 8.3 两条直线的位置关系(二) *创设情境 兴趣导入 【问题】 平面内两条既不重合又不平行的直线肯定相交.如何求交点的坐标呢? 图8-12 介绍 质疑 引导 分析 了解 思考 启发 学生思考 *动脑思考 探索新知 如图8-12所示,两条相交直线的交点,既在上,又在上.所以的坐标是两条直线的方程的公共解.因此解两条直线的方程所组成的方程组,就可以得到两条直线交点的坐标. 观察图8-13,直线、相交于点P,如果不研究终边相同的角,共形成四个正角,分别为、、、,其中与,与为对顶角,而且. 图8-13 我们把两条直线相交所成的最小正角叫做这两条直线的夹角,记作. 规定,当两条直线平行或重合时,两条直线的夹角为零角,因此,两条直线夹角的取值范围为. 显然,在图8-13中,(或)是直线、的夹角,即. 当直线与直线的夹角为直角时称直线与直线垂直,记做.观察图8-14,显然,平行于轴的直线与平行于轴的直线垂直,即斜率为零的直线与斜率不存在的直线垂直. 图8-14 讲解 说明 讲解 说明 引领 分析 仔细 分析 讲解 关键 词语 思考 思考 理解 思考 理解 记忆 带领 学生 分析 带领 学生 分析 引导 式启 发学 生得 出结 果
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点
【高教版】中职数学拓展模块:1.2《正弦型函数》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.2正弦型函数. *创设情境 兴趣导入 与正弦函数图像的做法类似,可以用“五点法”作出正弦型函数的图像.正弦型函数的图像叫做正弦型曲线. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 5*巩固知识 典型例题 例3 作出函数在一个周期内的简图. 分析 函数与函数的周期都是,最大值都是2,最小值都是-2. 解 为求出图像上五个关键点的横坐标,分别令,,,,,求出对应的值与函数的值,列表1-1如下: 表 001000200 以表中每组的值为坐标,描出对应五个关键点(,0)、(,2)、(,0)、(,?2)、(,0).用光滑的曲线联结各点,得到函数在一个周期内的图像(如图). 图 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 15

【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 我们知道,在直角三角形(如图)中,,,即 ,, 由于,所以,于是 . 图1-6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中,是否也存在类似的数量关系呢? c 图1-7 当三角形为钝角三角形时,不妨设角为钝角,如图所示,以为原点,以射线的方向为轴正方向,建立直角坐标系,则 两边取与单位向量的数量积,得 由于设与角A,B,C相对应的边长分别为a,b,c,故 即 所以 同理可得 即 当三角形为锐角三角形时,同样可以得到这个结论.于是得到正弦定理: 在三角形中,各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题: (1)已知三角形的两个角和任意一边,求其他两边和一角. (2)已知三角形的两边和其中一边所对角,求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.

【高教版】中职数学拓展模块:3.3《离散型随机变量及其分布》教学设计
重点分析:本节课的重点是离散型随机变量的概率分布,难点是理解离散型随机变量的概念. 离散型随机变量 突破难点的方法: 函数的自变量 随机变量 连续型随机变量 函数可以列表 X123456p 2 4 6 8 10 12

高教版中职数学基础模块下册:10.1《计数原理》教学设计
授课 日期 班级16高造价 课题: §10.1 计数原理 教学目的要求: 1.掌握分类计数原理与分步计数原理的概念和区别; 2.能利用两个原理分析和解决一些简单的应用问题; 3.通过对一些应用问题的分析,培养自己的归纳概括和逻辑判断能力. 教学重点、难点: 两个原理的概念与区别 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》、课件 授课执行情况及分析: 板书设计或授课提纲 §10.1 计数原理 1、加法原理 2、乘法原理 3、两个原理的区别
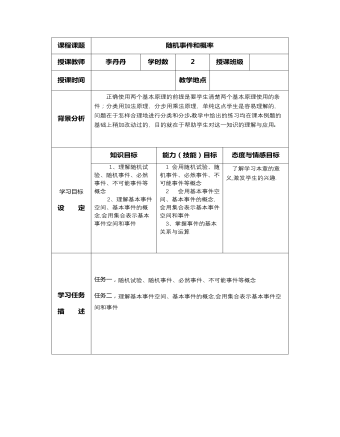
高教版中职数学基础模块下册:10.2《概率》教学设计
课程课题随机事件和概率授课教师李丹丹学时数2授课班级 授课时间 教学地点 背景分析正确使用两个基本原理的前提是要学生清楚两个基本原理使用的条件;分类用加法原理,分步用乘法原理,单纯这点学生是容易理解的,问题在于怎样合理地进行分类和分步教学中给出的练习均在课本例题的基础上稍加改动过的,目的就在于帮助学生对这一知识的理解与应用 学习目标 设 定知识目标能力(技能)目标态度与情感目标1、理解随机试验、随机事件、必然事件、不可能事件等概念 2、理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件 1 会用随机试验、随机事件、必然事件、不可能事件等概念 2 会用基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件 3、掌握事件的基本关系与运算 了解学习本章的意义,激发学生的兴趣. 学习任务 描 述 任务一,随机试验、随机事件、必然事件、不可能事件等概念 任务二,理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件

人教版高中历史必修2从“战时共产主义”到“斯大林模式”说课稿2篇
【课堂小结】本课主要讲述俄国十月革命后进行经济建设,并在建设中进行社会主义探索,期间先后出现了战时共产主义政策、新经济政策和斯大林模式,这些政策和体制的产生都是历史和当时现实有关,但也反映出在建设社会主义中既有成功的也由重大失误,主要在于缺乏现成的政策和模式可供借鉴,更在于理论上的缺乏。斯大林模式的形成同苏联当时社会生产力的发展水平相适应,它在初期和战争时期曾发挥了巨大作用,使苏联成为强大的社会主义国家。它建立的高度集中的计划经济体制和新型的工业化模式是苏联进行社会主义建设中的探索和创新,对二战后社会主义国家产生了深刻影响,促进这些国家国民经济的恢复和发展,形成了足以同资本主义相抗衡的社会主义阵营。但是,它没有解决社会主义民主政治建设和经济运行的一系列根本问题,违背了列宁关于把文化经济建设当作工作重心的指示,仍把政治斗争放在第一位。

人教版高中历史必修2从“战时共产主义”到“斯大林模式”教案
5、弊端:(1)经济发展不均衡,片面发展重工业,使轻工业和农业长期处于落后状态;(2)对农民的剥夺太重,挫伤了农民的生产积极性;(3)长期执行指令性计划严重削弱了企业的生产自主权,不利于发挥企业的生产积极性,制约了苏联经济的可持续发展。(4)计划经济体制确立后,没有随着社会的变化进行调整,二战后逐渐僵化,丧失了自我完善的功能,成为苏联解体的重要因素。【合作探究】斯大林模式的评价及经验教训:积极:①使苏联迅速实现了 工业化②苏联经济实力的迅速增长,为反法西斯战争的胜利奠定了 物质基础 。消极:①政治:高度集权,破坏了 民主与法制 ; ②经济:优先发展重工业使 农业和轻工业长期处于落后状态,农民生产积极性不高;计划指令,压制了地方和企业的积极性,阻碍苏联经济的发展高度集中的计划经济体制,成为东欧剧变和苏联解体的重要原因。

人教A版高中数学必修一函数模型的应用教学设计(2)
本节通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用,进一步认识到函数是描述客观世界变化规律的基本数学模型,能初步运用函数思想解决一些生活中的简单问题。课程目标1.能利用已知函数模型求解实际问题.2.能自建确定性函数模型解决实际问题.数学学科素养1.数学抽象:建立函数模型,把实际应用问题转化为数学问题;2.逻辑推理:通过数据分析,确定合适的函数模型;3.数学运算:解答数学问题,求得结果;4.数据分析:把数学结果转译成具体问题的结论,做出解答;5.数学建模:借助函数模型,利用函数的思想解决现实生活中的实际问题.重点:利用函数模型解决实际问题;难点:数模型的构造与对数据的处理.

人教A版高中数学必修一函数模型的应用教学设计(1)
本节课选自《普通高中课程标准实验教科书数学必修1本(A版)》的第五章的4.5.3函数模型的应用。函数模型及其应用是中学重要内容之一,又是数学与生活实践相互衔接的枢纽,特别在应用意识日益加深的今天,函数模型的应用实质是揭示了客观世界中量的相互依存有互有制约的关系,因而函数模型的应用举例有着不可替代的重要位置,又有重要的现实意义。本节课要求学生利用给定的函数模型或建立函数模型解决实际问题,并对给定的函数模型进行简单的分析评价,发展学生数学建模、数学直观、数学抽象、逻辑推理的核心素养。1. 能建立函数模型解决实际问题.2.了解拟合函数模型并解决实际问题.3.通过本节内容的学习,使学生认识函数模型的作用,提高学生数学建模,数据分析的能力. a.数学抽象:由实际问题建立函数模型;b.逻辑推理:选择合适的函数模型;c.数学运算:运用函数模型解决实际问题;

人教版高中数学选修3一元线性回归模型及其应用教学设计
1.确定研究对象,明确哪个是解释变量,哪个是响应变量;2.由经验确定非线性经验回归方程的模型;3.通过变换,将非线性经验回归模型转化为线性经验回归模型;4.按照公式计算经验回归方程中的参数,得到经验回归方程;5.消去新元,得到非线性经验回归方程;6.得出结果后分析残差图是否有异常 .跟踪训练1.一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了6组观测数据列于表中: 经计算得: 线性回归残差的平方和: ∑_(i=1)^6?〖(y_i-(y_i ) ?)〗^2=236,64,e^8.0605≈3167.其中 分别为观测数据中的温度和产卵数,i=1,2,3,4,5,6.(1)若用线性回归模型拟合,求y关于x的回归方程 (精确到0.1);(2)若用非线性回归模型拟合,求得y关于x回归方程为 且相关指数R2=0.9522. ①试与(1)中的线性回归模型相比较,用R2说明哪种模型的拟合效果更好 ?②用拟合效果好的模型预测温度为35℃时该种药用昆虫的产卵数.(结果取整数).

海南省2016年中考语文真题(含解析)
醉翁亭记(选段)欧阳修①若夫日出而林霏开,云归而岩穴暝,晦明变化者,山间之朝暮也。野芳发而幽香,佳木秀而繁阴,风霜高洁,水落而石出者,山间之四时也。朝而往,暮而归,四时之景不同,而乐亦无穷也。②至于负者歌于途,行者休于树,前者呼,后者应,伛偻提携,往来而不绝者,滁人游也。临溪而渔,溪深而鱼肥,酿泉为酒,泉香而酒洌,山肴野蔌,杂然而前陈者,太守宴也。宴酣之乐,非丝非竹,射者中,弈者胜,觥筹交错,起坐而喧哗者,众宾欢也。苍颜白发,颓然乎其间者,太守醉也。

2022年陕西省中考语文真题(解析版)
神舟十二号飞行乘组出征太空,让很多青少年对航天事业燃起了强烈的兴趣和好奇心。中国青年报社对2047名14-35岁青少年进行了专项调查,结果图示如下:

安徽省2021年中考语文试题(解析版)
因为工作忙,在下班后、节假日,大部分时间都关在书房里读书写作,难得陪孩子,一直心怀歉疚。但歉疚时又一如既往地忙。实在心虚得自己都挺不过去了,就想为儿子做点事,( )一下,也安慰一下自己。

