-

请帮我一下吧 说课稿
一、教材分析《请帮我一下吧》是统编教材小学《道德与法治》一年级下册第四单元第14课,共有四个话题,本节课学习的是后两个话题《我会求助》和《温暖的“接力棒”》,主要是引导学生学习如何向人求助,领悟帮助他人的价值与意义,旨在引导学生懂得生活中受助于人和帮助别人,体会在和谐互助的社会生活的温暖。二、学情分析学会求助的基本技能,懂得不仅要能,懂得感恩,也要学会帮助他人,让友爱与互助精神得到传递养成互相帮助的好习惯,为学生的健康成长奠定基础。一年级的学生年纪小,独立性相对较差,他们在家中备受宠爱,很多家长对孩子的生活、学习等事务都一手包办,以至于遇到困难时有的过度依赖,有的不愿意向别人求助,有的不敢向别人求助。因此,要通过有效的教学,帮助引导学生学会求助,懂得互帮互助。三、教学目标与重难点基于教材、学情的分析,以及对小学道德与法治课程的理解,我确定了本节课的教学目标与重难点。教学目标我确定了三个。1.学会求助的基本技能。2.懂得互相帮助的价值和意义。3. 养成互相帮助的好习惯。

奖励一下自己? 说课稿
一、说教材本课是二年级《道德与法治》第四单元最后一课,通过两年的学习,每个学生都获得不同程度的进步和成长,所以这一课依据课程标准“愉快、积极地生活”,旨在引导学生对此进行梳理总结,发现自己的优点和长处,并为自己在学习中取得的进步感到高兴和自豪,确立成长的自信,以此激励自己不断进步。同时,引导学生过有计划的生活,明确自己下一步发展任务,以积极地心态、有准备地面对中年级的过渡。 说学情: 本课主要引导学生对自己两年来的成长与进步进行梳理与总结,总结具有抽象性和概括性,对低年级的学生来说,具有一定的难度。两年的时间,跨度长,如何有效引导进行比较;如何准确发现目前存在的问题,不是简单地文本迁移并将抽象的发展目标落实为具体的能力发展,都是在教学中需要解决的问题。二、说教学目标: 1、学会根据自己所做的正确事,来奖励自己; 2、不只是奖励自己,还要学会奖励周围的同学,伙伴; 3、我们都有需要努力的地方,学会设个未来奖,争取以后做的更好。 教学重难点:学会根据自己所做的正确事,来奖励自己,还要学会奖励周围的同学,伙伴

人教版高中政治必修4第九课唯物辩证法的实质和核心精品教案
a矛盾的同一性是矛盾双方相互吸引、相互联结的属性和趋势。它有两方面的含义:一是矛盾双方相互依赖,一方的存在以另一方的存在为前提,双方共处于一个统一体中;同一事物都有对立面和统一面两个方面,一方的存在以另一方为条件,彼此谁都离不开谁(形影想随、一个巴掌拍不响、不是冤家不聚头)。【举例】P67漫画:他敢剪吗?悬挂在山崖上的两个人构成一种动态的平衡。【举例】磁铁(S极和N极);没有上就没有下、没有香就没有臭、没有福就无所谓祸;【举例】父子关系(父亲之所以是父亲,因为有儿子,儿子之所以是儿子,因为有父亲);师生关系;二是矛盾双方相互贯通,即相互渗透、相互包含,在一定条件下可以相互转化。 【相关衔接】P68生物变性现象,雌雄转化现象【举例】生产与消费具有直接统一性

镇2024年第一季度政务公开工作总结和下一步工作计划
三、下一步工作计划(一)加强组织领导。高度重视政府信息公开工作,坚持将政府信息和政务公开工作作为部门工作的一项重要内容进行布置并狠抓计划落实,在工作中加强统筹领导,形成纵向到底、横向到边、上下联动、整体推进的工作体系。(二)定期开展自查。对日常测评反馈的问题,及时进行整改。对照考核指标认真梳理政务公开各项指标,及时发现和处理工作中发现的问题,有力推进政府信息公开工作的有效落实,为经济社会发展营造良好氛围。(三)强化信息报送。对第一季度中有7篇信息没有审核通过的原因进行深刻反思,在今后的信息报送工作中,将更加聚焦主责主业,围绕工作重点,及时总结经验,提炼亮点,加强审核,保证时效性、准确性和安全性,推动信息工作不断前进。
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
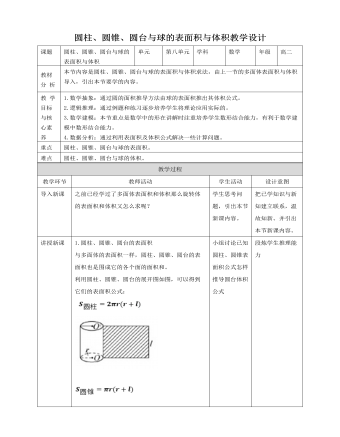
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教版高中数学选择性必修二等差数列的前n项和公式(1)教学设计
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献. 问题1:为什么1+100=2+99=…=50+51呢?这是巧合吗?试从数列角度给出解释.高斯的算法:(1+100)+(2+99)+…+(50+51)= 101×50=5050高斯的算法实际上解决了求等差数列:1,2,3,…,n,"… " 前100项的和问题.等差数列中,下标和相等的两项和相等.设 an=n,则 a1=1,a2=2,a3=3,…如果数列{an} 是等差数列,p,q,s,t∈N*,且 p+q=s+t,则 ap+aq=as+at 可得:a_1+a_100=a_2+a_99=?=a_50+a_51问题2: 你能用上述方法计算1+2+3+… +101吗?问题3: 你能计算1+2+3+… +n吗?需要对项数的奇偶进行分类讨论.当n为偶数时, S_n=(1+n)+[(2+(n-1)]+?+[(n/2+(n/2-1)]=(1+n)+(1+n)…+(1+n)=n/2 (1+n) =(n(1+n))/2当n为奇数数时, n-1为偶数

人教版高中数学选择性必修二等比数列的前n项和公式 (1) 教学设计
新知探究国际象棋起源于古代印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦粒的质量为40克,据查,2016--2017年度世界年度小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.问题1:每个格子里放的麦粒数可以构成一个数列,请判断分析这个数列是否是等比数列?并写出这个等比数列的通项公式.是等比数列,首项是1,公比是2,共64项. 通项公式为〖a_n=2〗^(n-1)问题2:请将发明者的要求表述成数学问题.

人教版高中数学选择性必修二等比数列的前n项和公式 (2) 教学设计
二、典例解析例10. 如图,正方形ABCD 的边长为5cm ,取正方形ABCD 各边的中点E,F,G,H, 作第2个正方形 EFGH,然后再取正方形EFGH各边的中点I,J,K,L,作第3个正方形IJKL ,依此方法一直继续下去. (1) 求从正方形ABCD 开始,连续10个正方形的面积之和;(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?分析:可以利用数列表示各正方形的面积,根据条件可知,这是一个等比数列。解:设正方形的面积为a_1,后续各正方形的面积依次为a_2, a_(3, ) 〖…,a〗_n,…,则a_1=25,由于第k+1个正方形的顶点分别是第k个正方形各边的中点,所以a_(k+1)=〖1/2 a〗_k,因此{a_n},是以25为首项,1/2为公比的等比数列.设{a_n}的前项和为S_n(1)S_10=(25×[1-(1/2)^10 ] )/("1 " -1/2)=50×[1-(1/2)^10 ]=25575/512所以,前10个正方形的面积之和为25575/512cm^2.(2)当无限增大时,无限趋近于所有正方形的面积和

人教版高中数学选择性必修二等差数列的前n项和公式(2)教学设计
课前小测1.思考辨析(1)若Sn为等差数列{an}的前n项和,则数列Snn也是等差数列.( )(2)若a1>0,d<0,则等差数列中所有正项之和最大.( )(3)在等差数列中,Sn是其前n项和,则有S2n-1=(2n-1)an.( )[答案] (1)√ (2)√ (3)√2.在项数为2n+1的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则n等于( )A.9 B.10 C.11 D.12B [∵S奇S偶=n+1n,∴165150=n+1n.∴n=10.故选B项.]3.等差数列{an}中,S2=4,S4=9,则S6=________.15 [由S2,S4-S2,S6-S4成等差数列得2(S4-S2)=S2+(S6-S4)解得S6=15.]4.已知数列{an}的通项公式是an=2n-48,则Sn取得最小值时,n为________.23或24 [由an≤0即2n-48≤0得n≤24.∴所有负项的和最小,即n=23或24.]二、典例解析例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?分析:将第1排到第20排的座位数依次排成一列,构成数列{an} ,设数列{an} 的前n项和为S_n。

人教版高中政治必修2国际社会的成员:主权国家和国际组织教案
(1)1945.10.24日,《联合国宪章》生效,联合国正式成立。主要机构有:联合国大会、安全理事会、经济及社会理事会、托管理事会、国际法院、秘书处等。(2)联合国的宗旨:维护国际和平与安全;发展国际间以尊重人民平等权利及自决原则为基础的友好关系;促进国际合作,以解决国际间属于经济、社会、文化及人类福利性质的国际问题;作为协调各国活动的中心。简单地说,就是维护国际和平与安全,促进国际合作与发展。(3)联合国的原则:各会员国主权平等,履行宪章规定的义务,以和平方式解决国际争端,不得对其他国家进行武力威胁或使用武力,集体协作,不干涉任何国家的内政,确保非会员国遵守上述原则。(4)联合国的作用:联合国在维护世界和平与安全,促进经济、社会的发展,以及实行人道主义援助等方面发挥着积极作用。

人教版高中政治必修4第二课百舸争流的思想教案
不可知论是否认人们认识世界或彻底改造世界的可能性的哲学学说。此概念首先由英国的赫胥黎(1825—1895)于1869年提出,不可知论的思想在古代就已产生,欧洲近代的主要代表是休谟和康德。其本质是把人的感觉看作是主观和客观之间的屏障而不是桥梁,不承认在感觉之外有确实可靠的客观外部世界的存在,不懂得认识过程中本质与现象、有限与无限的辩证关系。对不可知论最有力的驳斥是实践。有时不可知论一词也用以专指针对宗教教义而提出的一种学说,认为上帝是否存在、灵魂是否不朽是不可知的。2.二元论二元论是认为世界有两个本原的哲学学说,与一元论相对立,它把物质和意识绝对对立起来,认为物质和意识是两个各自独立、相互平行发展着的实体,谁也不产生谁,谁也不决定谁,都是世界的本原。它的观点是错误的:它肯定精神不依赖于物质而独立存在,这本身就是唯心主义的观点;它虽然承认物质是独立的本原,但在说明物质和精神的关系时,又把精神说成是唯一具有能动性的力量,必然倒向唯心主义。主要代表人物是法国的笛卡儿和德国的康德。

人教版高中政治必修3第二课文化对人的影响精品教案
民族精神是一个民族赖以生存和发展的精神支撑。一个民族,没有振奋的精神和高尚的品格,不可能自立于世界民族之林。“铁人”精神是“爱国、创业、求实、奉献”的大庆精神的典型化、人格化。其主要方面包括:“为祖国分忧、为民族争气”的爱国主义精神;为“早日把中国石油落后的帽子甩到太平洋里去”,“宁肯少活二十年,拼命也要拿下大油田”的忘我拼搏精神;干事业“有条件要上,没有条件创造条件也要上”的艰苦奋斗精神;“要为油田负责一辈子”,“干工作要经得起子孙万代检查”,对工作精益求精,为革命“练一身硬功夫、真本事”的科学求实精神;不计名利,不计报酬,埋头苦干的“老黄牛”精神;等等。40多年来,“铁人”精神早已家喻户晓,深入人心,成为大庆人的共同理想、信念和行为准则。“铁人”精神是对王进喜崇高思想、优秀品德的高度概括,体现了我国工人阶级精神风貌和中华民族传统美德的完美结合。“铁人”精神是战胜困难、勇往直前、不断取得新胜利的巨大精神力量。“铁人”精神是我们强大的精神支柱。

人教版高中政治必修4第二课百舸争流的思想精品教案
7、人总是按照自己对周围世界和人生的理解做事。有人认为命由天定,因而身处困境只是消极等待、逆来顺受;有人认为人定胜天,因而在困难面前积极奋争、不屈不挠。以上材料说明( )A哲学源于人们对实践的追问和对世界的思考B世界观决定方法论,方法论体现着世界观C哲学不等于自发的世界观D哲学是关于世界观的学说8、世界观和方法论的关系是()A世界观和方法论相互决定B方法论决定世界观,世界观体现方法论 C世界观决定方法论,方法论体现世界观 D世界观和方法论相互影响,相互决定9、下列关于哲学、世界观、具体知识之间联系的正确说法是()A哲学是关于世界观和具体知识的统一B哲学就是科学的世界观和具体知识C哲学是关于世界观的学说,是具体知识的概括和总结D哲学决定世界观,世界观决定具体知识10、下列对哲学的认识,不正确的是()A哲学是关于世界观的学说B哲学是世界观和方法论的统一C哲学是理论化、系统化、科学化的世界观D哲学是对具体知识的概括和总结

部编版语文八年级下册《庆祝奥林匹克运动复兴25周年》教案
2004年的雅典奥运会上,孔令辉获得冠军时忘情地亲吻胸前的国徽时,王军霞夺得金牌后激动的身披国旗绕运动场奔跑时,我们的泪水也会与领奖台上以手抚着胸前国徽高唱国歌的运动员的热泪一起落下。为了看体育比赛,我们甚至不惜守候到半夜而无怨无悔。在半夜看比赛时,我总在想:是什么让我们“为伊消得人憔悴”,为什么“总有一种力量让人泪流满面”。现在我有了答案:那是一种奥林匹克精神在激励着我们,在提升着我们。奥林匹克精神的内涵是丰富的。国际奥委会主席罗格在其就任宣言中指出:“奥林匹克的格言是更快、更高、更强。在新世纪来临的时候,或许对体育来讲需要新的格言,那就是更干净、更人性、更团结。” 奥林匹克精神让我们振奋,今天我们就来学习这篇课文《庆祝奥林匹克运动复兴25周年》。

人教部编版语文八年级下册庆祝奥林匹克运动复兴25周年教案
(3)推荐男女生代表各一位在全班进行演讲展示。 (4)围绕“讲”和“演”两方面的技巧,点评演讲效果。(生开展演讲活动,师指导)【设计意图】本环节通过集中梳理演讲技巧,并设计演讲技巧进行演讲展示,引导学生将理论知识逐步运用于具体的演讲实践中,提高学生的演讲能力。五、总结存储1.教师总结现代奥林匹克运动的创始人顾拜旦面对世界政治格局剧变的局面,以战略家的视野指出奥林匹克精神的内涵与价值,用诗歌般的语言阐述了奥林匹克平和自信的内涵,提出了奥林匹克运动的宗旨是教育,是面向大众,是促进和平、公平、公正。他激情澎湃地畅想美好前景,确信奥林匹克精神必将如阳光般普照大地。整篇演讲词站位高、格局广,语言庄重、典雅,值得我们用心体会。2.布置作业学校即将举行春季运动会,如果你被邀请在运动会的开幕式上作为学生代表发言,你将如何演讲?结合你对奥林匹克运动的精神的理解,写一篇300字左右的演讲词,并适当设计一些演讲技巧。

高教版中职数学基础模块下册:7.1《平面向量的概念及线性运算》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 7.1 平面向量的概念及线性运算 *创设情境 兴趣导入 如图7-1所示,用100N①的力,按照不同的方向拉一辆车,效果一样吗? 图7-1 介绍 播放 课件 引导 分析 了解 观看 课件 思考 自我 分析 从实例出发使学生自然的走向知识点 0 3*动脑思考 探索新知 【新知识】 在数学与物理学中,有两种量.只有大小,没有方向的量叫做数量(标量),例如质量、时间、温度、面积、密度等.既有大小,又有方向的量叫做向量(矢量),例如力、速度、位移等. 我们经常用箭头来表示方向,带有方向的线段叫做有向线段.通常使用有向线段来表示向量.线段箭头的指向表示向量的方向,线段的长度表示向量的大小.如图7-2所示,有向线段的起点叫做平面向量的起点,有向线段的终点叫做平面向量的终点.以A为起点,B为终点的向量记作.也可以使用小写英文字母,印刷用黑体表示,记作a;手写时应在字母上面加箭头,记作. 图7-2 平面内的有向线段表示的向量称为平面向量. 向量的大小叫做向量的模.向量a, 的模依次记作,. 模为零的向量叫做零向量.记作0,零向量的方向是不确定的. 模为1的向量叫做单位向量. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 带领 学生 分析 引导 式启 发学 生得 出结 果 10

高教版中职数学基础模块下册:7.1《平面向量的概念及线性运算》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 7.1 平面向量的概念及线性运算 *创设情境 兴趣导入 如图7-1所示,用100N①的力,按照不同的方向拉一辆车,效果一样吗? 图7-1 介绍 播放 课件 引导 分析 了解 观看 课件 思考 自我 分析 从实例出发使学生自然的走向知识点 0 3*动脑思考 探索新知 【新知识】 在数学与物理学中,有两种量.只有大小,没有方向的量叫做数量(标量),例如质量、时间、温度、面积、密度等.既有大小,又有方向的量叫做向量(矢量),例如力、速度、位移等. 我们经常用箭头来表示方向,带有方向的线段叫做有向线段.通常使用有向线段来表示向量.线段箭头的指向表示向量的方向,线段的长度表示向量的大小.如图7-2所示,有向线段的起点叫做平面向量的起点,有向线段的终点叫做平面向量的终点.以A为起点,B为终点的向量记作.也可以使用小写英文字母,印刷用黑体表示,记作a;手写时应在字母上面加箭头,记作. 图7-2 平面内的有向线段表示的向量称为平面向量. 向量的大小叫做向量的模.向量a, 的模依次记作,. 模为零的向量叫做零向量.记作0,零向量的方向是不确定的. 模为1的向量叫做单位向量. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 带领 学生 分析 引导 式启 发学 生得 出结 果 10

高教版中职数学基础模块下册:8.3《两条直线的位置关系》优秀教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 8.3 两条直线的位置关系(一) *创设情境 兴趣导入 【知识回顾】 我们知道,平面内两条直线的位置关系有三种:平行、相交、重合.并且知道,两条直线都与第三条直线相交时,“同位角相等”是“这两条直线平行”的充要条件. 【问题】 两条直线平行,它们的斜率之间存在什么联系呢? 介绍 质疑 引导 分析 了解 思考 启发 学生思考*动脑思考 探索新知 【新知识】 当两条直线、的斜率都存在且都不为0时(如图8-11(1)),如果直线平行于直线,那么这两条直线与x轴相交的同位角相等,即直线的倾角相等,故两条直线的斜率相等;反过来,如果直线的斜率相等,那么这两条直线的倾角相等,即两条直线与x轴相交的同位角相等,故两直线平行. 当直线、的斜率都是0时(如图8-11(2)),两条直线都与x轴平行,所以//. 当两条直线、的斜率都不存在时(如图8-11(3)),直线与直线都与x轴垂直,所以直线// 直线. 显然,当直线、的斜率都存在但不相等或一条直线的斜率存在而另一条直线的斜率不存在时,两条直线相交. 由上面的讨论知,当直线、的斜率都存在时,设,,则 两个方程的系数关系两条直线的位置关系相交平行重合 当两条直线的斜率都存在时,就可以利用两条直线的斜率及直线在y轴上的截距,来判断两直线的位置关系. 判断两条直线平行的一般步骤是: (1) 判断两条直线的斜率是否存在,若都不存在,则平行;若只有一个不存在,则相交. (2) 若两条直线的斜率都存在,将它们都化成斜截式方程,若斜率不相等,则相交; (3) 若斜率相等,比较两条直线的纵截距,相等则重合,不相等则平行. 讲解 说明 引领 分析 仔细 分析 讲解 关键 词语 思考 理解 思考 理解 带领 学生 分析 引导 式启 发学 生得 出结 果

高教版中职数学基础模块下册:9.2《直线与直线、直线与平面、平面与平面平行的判定》
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 9.2 直线与直线、直线与平面、平面与平面平行的判定与性质 *创设情境 兴趣导入 观察图9?13所示的正方体,可以发现:棱与所在的直线,既不相交又不平行,它们不同在任何一个平面内. 图9?13 观察教室中的物体,你能否抽象出这种位置关系的两条直线? 介绍 质疑 引导 分析 了解 思考 启发 学生思考 0 2*动脑思考 探索新知 在同一个平面内的直线,叫做共面直线,平行或相交的两条直线都是共面直线.不同在任何一个平面内的两条直线叫做异面直线.图9-13所示的正方体中,直线与直线就是两条异面直线. 这样,空间两条直线就有三种位置关系:平行、相交、异面. 将两支铅笔平放到桌面上(如图9?14),抬起一支铅笔的一端(如D端),发现此时两支铅笔所在的直线异面. 桌子 B A C D 两支铅笔 图9 ?14(请画出实物图) 受实验的启发,我们可以利用平面做衬托,画出表示两条异面直线的图形(如图9 ?15). (1) (2) 图9?15 利用铅笔和书本,演示图9?15(2)的异面直线位置关系. 讲解 说明 引领 分析 仔细 分析 关键 语句 思考 理解 记忆 带领 学生 分析 5



