-
人教A版高中数学必修一函数的应用（一）教学设计（2）
客观世界中的各种各样的运动变化现象均可表现为变量间的对应关系，这种关系常常可用函数模型来描述，并且通过研究函数模型就可以把我相应的运动变化规律.课程目标1、能够找出简单实际问题中的函数关系式，初步体会应用一次函数、二次函数、幂函数、分段函数模型解决实际问题； 2、感受运用函数概念建立模型的过程和方法，体会一次函数、二次函数、幂函数、分段函数模型在数学和其他学科中的重要性． 数学学科素养1.数学抽象：总结函数模型； 2.逻辑推理：找出简单实际问题中的函数关系式，根据题干信息写出分段函数； 3.数学运算：结合函数图象或其单调性来求最值. ； 4.数据分析：二次函数通过对称轴和定义域区间求最优问题； 5.数学建模：在具体问题情境中，运用数形结合思想，将自然语言用数学表达式表示出来。 重点：运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题；难点：运用函数思想理解和处理现实生活和社会中的简单问题．
人教A版高中数学必修一函数的零点与方程的解教学设计（2）
本章通过学习用二分法求方程近似解的的方法，使学生体会函数与方程之间的关系，通过一些函数模型的实例，让学生感受建立函数模型的过程和方法，体会函数在数学和其他学科中的广泛应用，进一步认识到函数是描述客观世界变化规律的基本数学模型，能初步运用函数思想解决一些生活中的简单问题。1.了解函数的零点、方程的根与图象交点三者之间的联系.2.会借助零点存在性定理判断函数的零点所在的大致区间.3.能借助函数单调性及图象判断零点个数．数学学科素养1.数学抽象：函数零点的概念；2.逻辑推理：借助图像判断零点个数；3.数学运算：求函数零点或零点所在区间；4.数学建模：通过由抽象到具体，由具体到一般的思想总结函数零点概念.重点：零点的概念，及零点与方程根的联系；难点：零点的概念的形成．
人教A版高中数学必修一集合间的基本关系教学设计（2）
第一节通过研究集合中元素的特点研究了元素与集合之间的关系及集合的表示方法，而本节重点通过研究元素得到两个集合之间的关系，尤其学生学完两个集合之间的关系后，一定让学生明确元素与集合、集合与集合之间的区别。课程目标1. 了解集合之间包含与相等的含义，能识别给定集合的子集．2. 理解子集.真子集的概念． 3. 能使用 图表达集合间的关系，体会直观图示对理解抽象概念的作用。数学学科素养1.数学抽象：子集和空集含义的理解；2.逻辑推理：子集、真子集、空集之间的联系与区别；3.数学运算：由集合间的关系求参数的范围，常见包含一元二次方程及其不等式和不等式组；4.数据分析：通过集合关系列不等式组， 此过程中重点关注端点是否含“=”及 问题；5.数学建模：用集合思想对实际生活中的对象进行判断与归类。
人教A版高中数学必修一简单的三角恒等变换教学设计（2）
它位于三角函数与数学变换的结合点上，能较好反应三角函数及变换之间的内在联系和相互转换，本节课内容的地位体现在它的基础性上。作用体现在它的工具性上。前面学生已经掌握了两角和与差的正弦、余弦、正切公式以及二倍角公式，并能通过这些公式进行求值、化简、证明，虽然学生已经具备了一定的推理、运算能力，但在数学的应用意识与应用能力方面尚需进一步培养.课程目标1.能用二倍角公式推导出半角公式，体会三角恒等变换的基本思想方法，以及进行简单的应用． 2.了解三角恒等变换的特点、变换技巧，掌握三角恒等变换的基本思想方法． 3.能利用三角恒等变换的技巧进行三角函数式的化简、求值以及证明，进而进行简单的应用． 数学学科素养1.逻辑推理： 三角恒等式的证明； 2.数据分析：三角函数式的化简； 3.数学运算：三角函数式的求值.
人教A版高中数学必修一全称量词与存在量词教学设计（2）
(4)“不论m取何实数,方程x2+2x-m=0都有实数根”是全称量词命题,其否定为“存在实数m0,使得方程x2+2x-m0=0没有实数根”,它是真命题.解题技巧：（含有一个量词的命题的否定方法）(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称量词命题还是存在量词命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.跟踪训练三3．写出下列命题的否定,并判断其真假:(1)p:?x∈R,x2-x+ ≥0;(2)q:所有的正方形都是矩形;(3)r:?x∈R,x2+3x+7≤0;(4)s:至少有一个实数x,使x3+1=0.【答案】见解析【解析】(1) p:?x∈R,x2-x+1/4<0.∵?x∈R,x2-x+1/4=(x"-" 1/2)^2≥0恒成立,∴ p是假命题.
人教A版高中数学必修一用二分法求方程的近似解教学设计（2）
本节通过学习用二分法求方程近似解的的方法，使学生体会函数与方程之间的关系，通过一些函数模型的实例，让学生感受建立函数模型的过程和方法，体会函数在数学和其他学科中的广泛应用，进一步认识到函数是描述客观世界变化规律的基本数学模型，能初步运用函数思想解决一些生活中的简单问题。课程目标1.了解二分法的原理及其适用条件.2.掌握二分法的实施步骤.3.通过用二分法求方程的近似解，使学生体会函数零点与方程根之间的联系，初步形成用函数观点处理问题的意识.数学学科素养1.数学抽象：二分法的概念；2.逻辑推理：用二分法求函数零点近似值的步骤；3.数学运算：求函数零点近似值；4.数学建模：通过一些函数模型的实例，让学生感受建立函数模型的过程和方法，体会函数在数学和其他学科中的广泛应用.
人教A版高中数学必修一正弦函数、余弦函数的图像教学设计（2）
由于三角函数是刻画周期变化现象的数学模型，这也是三角函数不同于其他类型函数的最重要的地方，而且对于周期函数，我们只要认识清楚它在一个周期的区间上的性质，那么它的性质也就完全清楚了，因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图，从画出的图形中观察得出五个关键点，得到“五点法”画正弦函数、余弦函数的简图．课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法，能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系. 数学学科素养1.数学抽象：正弦曲线与余弦曲线的概念； 2.逻辑推理：正弦曲线与余弦曲线的联系； 3.直观想象：正弦函数余弦函数的图像； 4.数学运算：五点作图； 5.数学建模：通过正弦、余弦图象图像，解决不等式问题及零点问题，这正是数形结合思想方法的应用.
人教A版高中数学必修一正弦函数、余弦函数的性质教学设计（2）
本节课是正弦函数、余弦函数图像的继续，本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象：理解周期函数、周期、最小正周期等的含义； 2.逻辑推理： 求正弦、余弦形函数的单调区间；3.数学运算：利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模：让学生借助数形结合的思想，通过图像探究正、余弦函数的性质.重点：通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质； 难点：应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.
人教A版高中数学必修一指数函数的概念教学设计（2）
指数函数与幂函数是相通的，本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念，通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景；2、理解指数函数的概念和意义.数学学科素养1.数学抽象：指数函数的概念；2.逻辑推理：用待定系数法求函数解析式及解析值；3.数学运算：利用指数函数的概念求参数；4.数学建模：通过由抽象到具体，由具体到一般的思想总结指数函数概念.重点：理解指数函数的概念和意义；难点：理解指数函数的概念．教学方法：以学生为主体，采用诱思探究式教学，精讲多练。教学工具：多媒体。一、 情景导入在本章的开头，问题（1）中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求：让学生自由发言，教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修一正切函数的图像与性质教学设计（2）
本节课是三角函数的继续，三角函数包含正弦函数、余弦函数、正切函数.而本课内容是正切函数的性质与图像.首先根据单位圆中正切函数的定义探究其图像，然后通过图像研究正切函数的性质. 课程目标1、掌握利用单位圆中正切函数定义得到图象的方法;2、能够利用正切函数图象准确归纳其性质并能简单地应用.数学学科素养1.数学抽象：借助单位圆理解正切函数的图像； 2.逻辑推理： 求正切函数的单调区间；3.数学运算：利用性质求周期、比较大小及判断奇偶性.4.直观想象：正切函数的图像； 5.数学建模：让学生借助数形结合的思想，通过图像探究正切函数的性质. 重点：能够利用正切函数图象准确归纳其性质并能简单地应用； 难点：掌握利用单位圆中正切函数定义得到其图象.
《卖懒》教学设计教案
1.制作红灯笼师：（展示漂亮的灯笼）小朋友们想不想自己亲手制作一个呢？生：好呀师：那小朋友们知道制作灯笼需要什么材料吗？生：彩纸、剪刀...师：没错，那老师先来展示一下怎么制作灯笼吧！（展示完后，开始让小朋友两两组合共同制作）2.制作灯笼剪纸师：小朋友们，刚刚是不是已经制作灯笼了呀？下面我们进行一个更好玩的环节？生：好呀好呀！师：那我先来展示一下咯，小朋友们别眨眼呀！（展示完后，开始让小朋友们独立完成）小结：通过制作共同合作制作灯笼与独自完成灯笼剪影，不仅使他们更能感知灯笼的形状，更能提高小朋友们的动手能力和思考力。
《琵琶行》教学设计
文本分析《琵琶行》作为白居易最为出名的诗歌之一，内容详实，情感动人，在诗歌中，白居易塑造了两个形象极为鲜明的人物——琵琶女&作者本人。一个是江湖薄命人，一个是官场失意者。两个本无交集的人因为京都琵琶声相遇，互诉衷肠后，发出“同是天涯沦落人，相逢何必曾相识“的感慨
人教版高中地理选修2中、低产田的综合治理教案
一、低湿地的治理与开发1、 低湿地治理开发的原因——辛店洼自然条件的主要特点（1）地势低平：辛店洼洼底海拔17．5米，洼缘海拔19．5米，是全市最低点。（2）渍涝严重：其成因如表6-4所示（3）土质好、水源足、水质好：成土母质为黄河冲积物，土壤质地好；水资源丰富，水质较好。2、低洼地治理开发的方法：鱼塘——台田模式（或称塘田模式）以往辛店洼曾采用挖沟排水的措施治理低洼地，但治理效果不明显，因为辛店洼的主要矛盾是地势低洼，地下水位高，挖沟排水因地势低，排水困难，地下水位难以下降，故治理效果不明显。20世纪80年代以来，科学工作者在辛店洼地区开始了整治低湿地的研究，他们遵循“因洼制宜”的指导思想，逐步摸索出了低湿地的治理模式：鱼塘—--台田模式
人教版高中地理选修2百万移民及其安置教案
三峡库区农村移民安置根本出路是通过发展大农业来解决耕地不足，不应盲目开垦荒坡地，防止产生新的水土流失，尽量避免生态环境恶化。2、就地后靠，就近安置模式三峡库区淹没区线状分布的受淹特点有别于一般水库淹没区的片状分布，使得库区移民具有相对分散的特点，且淹没涉及的356个乡镇没有一个被全淹，甚至全淹的村也很少，这有利于移民在本县甚至本乡就近后靠安置，避免了水库移民大量外迁、远迁所造成的种种困难和后遗症。三峡移民搬迁大多可以就地后靠，就近安置，这是三峡移民的一大特色。就近后靠安置的优点是不离本乡本土，移民容易接受，且避免了移民大量外迁、远迁所造成的困难和后遗症；缺点是容易对当地的生态环境造成过大的压力，如过度开垦坡地、破坏植被、加剧水土流失等。3、工程周期长，可从容安置移民三峡工程建设周期长（1994年～2009年，共17年），使得移民安置能够及早进行，可以从容安置移民的生产和生活。
人教版高中地理选修2荒漠化的成因与防治教案
1、图4.10“西北地区土地荒漠化的人为因素（以风力作用为例）图”产生荒漠化的人为因素有过度农垦、过度放牧、过度樵采和不合理利用水资源等。从荒漠化和人类的关系来看，荒漠化的发生、发展和社会经济有着密切的联系，人类不合理的经济活动不仅是荒漠化发生的主要原因和活跃因素，同时人类又是它的直接受害者。2、图4.14“荒漠植物的生态适应图”荒漠植物的生态适应特征表现在：a类为肉质植物，体内薄壁组织可储存大量水分，其近地表分布的根系可以在偶然而短暂的降水过程（如暴雨）中收集水分；b类植物一方面利用其近地表根系吸收可能的降水，另一方面根系向纵深发展，以利用稳定的地下水；c类为微叶或无叶型植物，叶片强烈缩小或退化，由绿色叶茎行使光合作用功能，蒸腾很弱。【教学内容】一、荒漠化的成因1．荒漠化的自然原因荒漠化的自然原因包括干旱（基本条件）、地表物质松散（物质基础）和大风吹扬（动力因素）。
人教版高中地理选修2我国的三大自然区教案
1、中国三大自然区的空间位置和基本特征。2、中国自然区域差异对人类活动的影响。◆重要图释图1.1“三大自然区图”三大自然区的界线（自然地理分界）：西北干旱半干旱区与东部季风区之间大致以400mm等年降水量线为界，青藏高寒区与东部季风区约以3000米等高线为界，青藏高寒区与西北干旱半干旱区以昆仑山——阿尔金山——祁连山为界。【学习策略】1、读图分析：通过读图、分析、归纳的方法，识记三大自然区的空间位置、相互界线，理解各自然地理要素的特征和空间分布规律。2、综合训练：运用空白地图，将地理事物落实在图上，并进行比较分析、归纳整理，理解三大自然区的区域差异。【教学内容】一、三大自然区的划分1．三大自然区的划分依据（地貌、气候的地域差异）
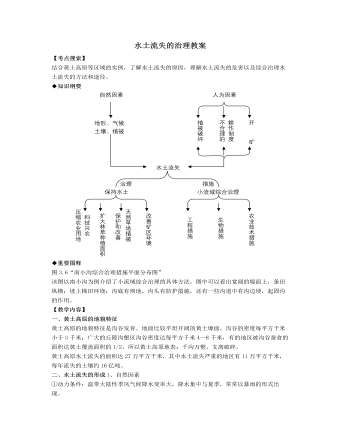
人教版高中地理选修2水土流失的治理教案
2、关于黄土高原小流域及其治理的叙述，正确的是()A.小流域不能看作是一个完整的地域单元B.小流域可以相当于黄土高原上一条河流的整个流域C.小流域综合治理的方针是“保塬、护坡、固沟“D.小流域的综合治理只能采用农业技术措施3、黄土高原植被遭到破坏的原因有()①营造宫殿，毁林开荒②修筑梯田，开石动土③开荒弃荒，轮荒作业④开露天矿，建隔离护坝⑤保塬护坡，打坝建库⑥开挖原生地面，复垦采空矿区A.①②④B.①③⑤C.①③D.②④4、下列关于黄土高原的叙述，正确的是()A.水土流失不可治理B.人为因素是黄土高原现代水土流失的主导因素C.植树种草是做好水土保持的基本前提D.开矿会加剧水土流失，故应少开矿5、引起黄土高原水土流失最直接的因素是()A.降水集中于夏季且多暴雨B.黄土垂直节理发育C.地表崎岖不平，千沟万壑D.不合理开发造成地表黄土裸露，失去植被保护6、治理黄土高原水土流失的工程措施有()A.植树造林B.平整土地C.修建水库D.深耕改土
高中教学学期工作计划
三、主要工作： 本学期教务处继续抓好教学管理，规范教学过程，加强教学指导，加大考核力度。群策群力、千方百计提高教学质量。 1、抓好常规教学的管理 ⑴、切实把好教学流程，规范教学秩序。上课期间(包括上晚辅导期间)禁止使用多媒体播放与教学无关的视频影像。 ⑵、规范教学过程，对备课、上课、作业批改、课后辅导、单元验收、学科竞赛等明确要求，认真检查、指导。检查作业批改两次，教务处设专人检查，记录。
高中教师个人教学工作计划5篇
二、学情分析 在校领导的正确领导下，本学期我校生源比去年有了重大的变化.高一年级招收了400多名新生，学校带来了新的希望.然而，我清醒地认识到任重而道远的现实是，我校实验班分数线仅为140分，普通班入学成绩仍居附近各中学之末.要实现我校教学质量的根本性进步，非一朝一夕之功.实验班的教学当然是重中之重，而普通班又绝不能一弃了之.现在的学情与现实决定了并不是付出十分努力就一定有十分收获.但教师的责任与职业道德时刻提醒我，没有付出一定是没有收获的.作为新时代的教师，只有付出百倍的努力，苦干加巧干，才能对得起良心，对得起人民群众的期望.
人教版高中地理选修2建设上海浦东新区的地理背景教案
2、上海是全国最大的商业中心，上海港是全国最大的港口。商业中心区位选择因素与港口的区位选择因素的共性条件是（ ）A、自然地理条件B、经济地理条件C、地理位置D、经济腹地3、中国政府宣布开发上海浦东的时间是（ ）A、1978年B、1985年C、1989年D、1990年4、有关上海优越区位条件的叙述，错误的是（ ）A、长江三角洲可提供充足的农副产品B、是全国最大的交通枢纽C、是我国最大城市带的核心城市D、是我国面积最大的直辖市5、目前上海市面临的最主要的人口问题是（ ）A、人口老龄化，青壮年赡养照顾众多老人负担过重B、卫星城镇人口比重大C、人口基数大，自然增长率高D、人口年龄构成轻，生育高峰压力大6、城市问题产生的主要原因是（ ）A、城市规模扩大B、城市基础设施相对滞后C、城市管理混乱D、城市人口规模和经济规模的迅速扩大7、下列可反映上海市的城市问题的是（ ）A、上海市区人均道路面积略高于北京市区B、上海市沙尘暴天气多发C、上海市许多家庭三代人同室居住D、上海市人均绿地面积稍高于重庆