-

主题教育工作自评总结
五是抓实检视整改以刀刃向内的勇气深挖问题症结。迅速传达学习省委以案促改专项教育整治动员部署会议精神严格标XXXX要求把专项教育整治纳入主题教育检视整改梳理形成问题清单把整改责任落实到岗、化到人。把检视整改精准调研施策的切入点、破除发展壁垒言的突破口针指导组反馈的见建议、调查研究的突出问题和自查梳理的短板不足建立完善整改进度定期报告、问题清单跟踪销号等制度深入查摆分析拿出整改实招。六是抓实建章立制以制度机制的成效巩固深化成果。坚持从问题上找规律从制度上找漏洞着力构建符合省情实际、具有XXXX工特色的制度体系。与XXXX联合制定XXXX制度做好XXXX工、健全完善干部教育管理闭环体系制度支撑。组织力会议议事、调查研究、XXXX、XXXX等现行制度进行再梳理、再修订、再完善。不断大制度执行情况的检查指导力度把XXXX、XXXX单位制度制定和执行情况纳入XXXX系统年度考核有效增强制度的刚性约束。

秋冬疫情防控全市民政系统秋冬季新冠肺炎疫情防控工作方案应急预案
一、工作目标全市各级民政系统要充分认识秋冬疫情防控的重要性、长期性和艰巨性,强化底线思维、风险意识、问题导向,抓紧在民政系统内补短板、强弱项、堵漏洞,抓紧推进应对新冠肺炎秋冬季疫情防控的各项工作,严格有效防范疫情反弹。二、基本原则坚持疫情防控领导体制、战时机制、指挥体系不变,坚持常态化防控和局部应急处置相结合。按照“指令清晰、系统有序、条块畅达、执行有力”要求,进一步完善多点预警、应急指挥机制。针对疫情的不同风险等级和相应级别,提出应对处置意见和方案。在市疫情防控指挥部的统一领导下做好疫情防控工作。

第九周国旗下讲话稿:从自己做起 从现在做起 从细节做起 让廉洁之花在校园绽放
第九周国旗下讲话稿:从自己做起从现在做起从细节做起让廉洁之花在校园绽放敬爱的老师,亲爱的同学们,大家好!最近,《人民的名义》连续剧引了很多师生的关注。这部反腐题材的电视剧以曲折的故事情节,戏骨们的精湛表演受到了大家的热捧。这也反映出当前的反腐行动和廉洁教育深入人心。为了在我校进一步推进廉洁文化进校园活动,根据我校工作安排,今天我借此机会和大家一起分享廉洁文化进校园的思考。我的的题目是:从自己做起,从细节做起,从现在做起,让廉洁之花在校园绽放首先,同学们会问:什么是廉洁?什么是廉洁文化?屈原在《楚辞·招魂》说:“朕幼清以廉洁兮,身服义尔未末沫。”东汉学者王逸在《楚辞·章句》中注释说:“不受曰廉,不污曰洁。”也就是说不接受他人的馈赠的钱财礼物,不让自己清白的人品受到玷污,就是廉洁。廉洁文化是社会主义先进文化的重要组成部分,是廉洁的理论和行为方式及其相互关系的文化总和。它提倡廉洁自律,秉公办事,为人民服务,清白做人。它要求管理者廉洁自律,执政为民;从业人员爱岗敬业,遵纪守法;社会公共组织处事公道正派,诚实守信。

XX学年第一学期第8周国旗下讲话稿:运动与生命同在。青春与快乐永存
敬爱的老师们,亲爱的同学们:大家好,我是来自九年四班的叶佳蜜,今天我要演讲的主题是运动与生命同在。青春与快乐永存。无论是过去,现在,还是将来,健康一直是人们追求的永恒主题。生命在于运动,人生短短几十年,虽不长,但要承担的责任却很重,要做的事情却很多。健康的身体是多少人可望而不可得的梦想。健康的健康是正处于青春期的我们意气风发的保证。只有拥有健康的身体才能让我们的青春迸发出无限的激情和色彩。体育运动,多么骄傲,它让生命之树常青。生命给予运动以真实意义。每一细胞的组合,每一神经的连动,每一骨骼的存在,都穿起了运动的全部。生命,多么可贵,他让运动的高峰迭起,生命,多么值得珍惜,它让运动之火绚丽多姿。生命创造了运动,运动使青春快乐。可以说运动是非常重要的,自我校开创以来就非常注重体育运动。如自行车,柔道,还有最新的足球,小到日常的跑操,大道国家级的比赛,等等等等。

北师大版初中数学八年级下册一元一次不等式与一次函数说课稿2篇
由于任何一个一元一次不等式都能写成ax+b>0(或<0)的形式,而此式的左边与一次函数y=ax+b的右边一致,所以从变化与对应的观点考虑问题,解一元一次不等式也可以归结为两种认识:⑴从函数值的角度看,就是寻求使一次函数y=ax+b的值大于(或小于0)的自变量x的取值范围。⑵从函数图像的角度看,就是确定直线y=ax+b在x轴上(或下)方部分所有的点的横坐标所构成的集合。教学过程中,主要从以上两个角度探讨一元一次不等式与一次函数的关系。1、“动”―――学生动口说,动脑想,动手做,亲身经历知识发生发展的过程。2、“探”―――引导学生动手画图,合作讨论。通过探究学习激发强烈的探索欲望。3、“乐”―――本节课的设计力求做到与学生的生活实际联系紧一点,直观多一点,动手多一点,使学生兴趣高一点,自信心强一点,使学生乐于学习,乐于思考。4、“渗”―――在整个教学过程中,渗透用联系的观点看待数学问题的辨证思想。

国有企业2024年上半年工作汇报和下半年工作计划集团公司总结报告
(二)强化履约保障,打造高质量发展新引擎。一方面强化精准管控。针对年度产值完成压力较大项目,认真分析重要节点和关键难点,统筹优化劳动力及各项资源,积极协助项目“找问题、想措施、增产值”,实现“精确制导、精准施策”,进一步促进重点项目高效优质履约。另一方面加强分包管理。探索建立各企业、各地域劳务资源供应模式,优选劳务合作队伍,建立战略合作机制,打造“总包-分包利益共同体”。(三)提高运行质量,占领高质量发展新高地。一是全力压实清收清欠责任。针对当前清欠收款难的问题,公司召开专题会议明确领导班子责任分工和清欠收款指标,班子成员靠前指挥,力争在四季度实现新突破,加速资金回笼。二是全力压降成本费用。严格贯彻“方案决定成本”的理念,持续优化施工组织设计,确保方案领先;有针对性的强化各项结算措施,降低已竣未结存量、降低三年以上存量、降低历史遗留存量,在确保完成年度结算指标的基础上进一步扩大结算战果。

国有企业2024年上半年工作汇报和下半年工作计划(集团公司,总结报告)
(二)强化履约保障,打造高质量发展新引擎。一方面强化精准管控。针对年度产值完成压力较大项目,认真分析重要节点和关键难点,统筹优化劳动力及各项资源,积极协助项目“找问题、想措施、增产值”,实现“精确制导、精准施策”,进一步促进重点项目高效优质履约。另一方面加强分包管理。探索建立各企业、各地域劳务资源供应模式,优选劳务合作队伍,建立战略合作机制,打造“总包-分包利益共同体”。(三)提高运行质量,占领高质量发展新高地。一是全力压实清收清欠责任。针对当前清欠收款难的问题,公司召开专题会议明确领导班子责任分工和清欠收款指标,班子成员靠前指挥,力争在四季度实现新突破,加速资金回笼。二是全力压降成本费用。严格贯彻“方案决定成本”的理念,持续优化施工组织设计,确保方案领先;有针对性的强化各项结算措施,降低已竣未结存量、降低三年以上存量、降低历史遗留存量,在确保完成年度结算指标的基础上进一步扩大结算战果。三是全力提升创效能力。

教育质量专项调研报告_教育质量包括哪些方面
通过这次调研活动,从整体上看,在学校的努力下,吴家小学教育教学重过程、重实效、重改革、重创新,中心校“提升教育教学质量工程”的文件精神得到了较好的贯彻落实,该校在“坚持和落实质量形成过程的管理”、“重视学科建设,加强校本教研”、“立足课堂,全面推进课堂教学改革”、“打造学校特色品牌,全面实施素质教育”、“注重校风教风建设,培养学生习惯和品质”、“加强三跳项目,全面提高教育教学质量”等方面呈现出不少的特色和亮点,彰显了学校的个性。xx教育教学工作综合评估中,20**年被评为进步奖。这样优异的成绩证明了该校很多管理经验值得学习和推广。

教育质量专项调研报告_教育质量包括哪些方面
一、调研的工作目标 通过调研,了解我学区小学段教育教学的基本情况,总结被调研学校的教育教学质量提升的经验、方法,查找教育教学过程中存在的问题,寻求破解我学区小学段教育教学质量提升瓶颈的方法和策略,改进学校管理措施,促进教育教学常规管理科学化、规范化、精细化,全面提升我校教育教学质量。 二、调研的基本情况 1. 选取样本学校。 本次调研,为了使样本校抽样具有代表性,结合我校的现状,调研工作在我中心小学中选取了具有代表性的吴家英里小学作为样本校。

精编中学教师教学学习个人心得与感受参考范文
首先,要认真钻研教材,为“预设”打好基础。教材是教学资料的载体,每一位教师都要认真研读、感悟、领会教材,了解教材的基本精神和编写意图,把握教材所带给的数学活动的基本线索,分析教材所渗透的数学思想、方法和学生活动的科学内涵,这样才能体会新教材蕴含的教学理念,备出高质量的教学预案。 其次,要改变备课模式,变“教案”为“学案”。学生是学习的主人,一切知识经验的获得都依靠于学生的自主建构、自我内化。离开了“学”,再精心的“设计”也没有好处,教师要充分思考,预设学生可能出现的状况,并采取相应的对策。即对整个教学过程进行一种有准备、有意识的预设。

精编开展教师学习廉洁从教心得体会参考范文
第一、献身教育,为人师表 教师工作的性质是教书育人,我们每一位教师都应树立正确的幸福观,提高自己的认识能力,把教育作为一种崇高的事业放在首位,乐于奉献,为世人做出表率。现代伟大的人民教育家陶行知先生一生以“爱满天下”为座右铭,正是为了祖国未来无数的“瓦特”、“牛顿”、“爱迪生”,教师将满腔的爱尽情赋予了学生。论财产教师两袖清风,一无所有,但教师却富有,我们拥有无数学生对我们爱的回报。
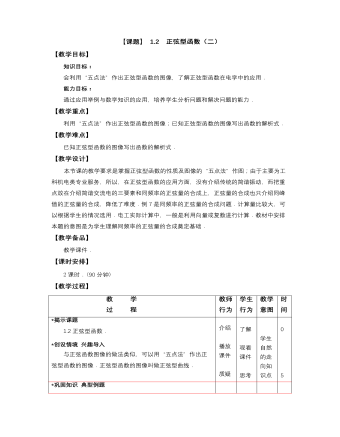
【高教版】中职数学拓展模块:1.2《正弦型函数》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.2正弦型函数. *创设情境 兴趣导入 与正弦函数图像的做法类似,可以用“五点法”作出正弦型函数的图像.正弦型函数的图像叫做正弦型曲线. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 5*巩固知识 典型例题 例3 作出函数在一个周期内的简图. 分析 函数与函数的周期都是,最大值都是2,最小值都是-2. 解 为求出图像上五个关键点的横坐标,分别令,,,,,求出对应的值与函数的值,列表1-1如下: 表 001000200 以表中每组的值为坐标,描出对应五个关键点(,0)、(,2)、(,0)、(,?2)、(,0).用光滑的曲线联结各点,得到函数在一个周期内的图像(如图). 图 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 15
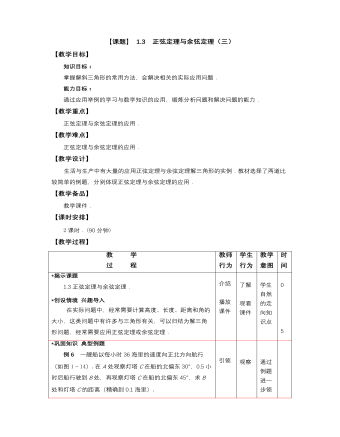
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.1《排列与组合》优秀教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 3.1 排列与组合. *创设情境 兴趣导入 基础模块中,曾经学习了两个计数原理.大家知道: (1)如果完成一件事,有N类方式.第一类方式有k1种方法,第二类方式有k2种方法,……,第n类方式有kn种方法,那么完成这件事的方法共有 = + +…+(种). (3.1) (2)如果完成一件事,需要分成N个步骤.完成第1个步骤有k1种方法,完成第2个步骤有k2种方法,……,完成第n个步骤有kn种方法,并且只有这n个步骤都完成后,这件事才能完成,那么完成这件事的方法共有 = · ·…·(种). (3.2) 下面看一个问题: 在北京、重庆、上海3个民航站之间的直达航线,需要准备多少种不同的机票? 这个问题就是从北京、重庆、上海3个民航站中,每次取出2个站,按照起点在前,终点在后的顺序排列,求不同的排列方法的总数. 首先确定机票的起点,从3个民航站中任意选取1个,有3种不同的方法;然后确定机票的终点,从剩余的2个民航站中任意选取1个,有2种不同的方法.根据分步计数原理,共有3×2=6种不同的方法,即需要准备6种不同的飞机票: 北京→重庆,北京→上海,重庆→北京,重庆→上海,上海→北京,上海→重庆. 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 15*动脑思考 探索新知 我们将被取的对象(如上面问题中的民航站)叫做元素,上面的问题就是:从3个不同元素中,任取2个,按照一定的顺序排成一列,可以得到多少种不同的排列. 一般地,从n个不同元素中,任取m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,时叫做选排列,时叫做全排列. 总结 归纳 分析 关键 词语 思考 理解 记忆 引导学生发现解决问题方法 20

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.

【高教版】中职数学拓展模块:3.3《离散型随机变量及其分布》教学设计
重点分析:本节课的重点是离散型随机变量的概率分布,难点是理解离散型随机变量的概念. 离散型随机变量 突破难点的方法: 函数的自变量 随机变量 连续型随机变量 函数可以列表 X123456p 2 4 6 8 10 12

人教版高中历史必修3文艺复兴和宗教改革说课稿2篇
师:在科学发展过程中,前一个理论体系的不完善之处,往往是新的研究和新的发现的突破口。开普勒之后,意大利天文学家伽利略创制了天文望远镜,用更加精确的观察继续发展和验证哥白尼创立的新天文学理论。除了用望远镜进行天文观察以外,伽利略还开始进行自然科学的实验研究,哪位同学能给大家讲一讲伽利略在比萨斜塔上所作的关于物体自由下落的实验?生:(讲述这一实验)师:所以,伽利略在科学方面更加重要的贡献是奠定了近代实验科学的基础。(2)实验科学和唯物主义师:伽利略从实践上开辟了实验科学的方法,而英国唯物主义哲学家培根则从理论上阐述了实验科学的方法——归纳法。培根和伽利略同被称为实验科学之父,培根还有一句影响深刻的名言:“知识就是力量”,表明了他注重知识,尊崇科学的精神。我们再来概括一下意大利哲学家布鲁诺的唯物主义思想,是否有同学可以简述布鲁诺的生平事迹?

空间向量基本定理教学设计人教A版高中数学选择性必修第一册
反思感悟用基底表示空间向量的解题策略1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.例2.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG=1/3 CD(1)证明:EF⊥B1C;(2)求EF与C1G所成角的余弦值.思路分析选择一个空间基底,将(EF) ?,(B_1 C) ?,(C_1 G) ?用基向量表示.(1)证明(EF) ?·(B_1 C) ?=0即可;(2)求(EF) ?与(C_1 G) ?夹角的余弦值即可.(1)证明:设(DA) ?=i,(DC) ?=j,(DD_1 ) ?=k,则{i,j,k}构成空间的一个正交基底.

倾斜角与斜率教学设计人教A版高中数学选择性必修第一册
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.延伸探究1 本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.解:由题意知(m"-" 1"-" 1)/(m+1"-" 2m)>0,解得1<m<2.延伸探究2 若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何?解:(1)由题意知(m"-" 1"-" 2m)/(m+1"-" 3m)=1,解得m=2.(2)由题意知m+1=3m,解得m=1/2.直线斜率的计算方法(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.(2)若两点的横坐标不相等,则可以用斜率公式k=(y_2 "-" y_1)/(x_2 "-" x_1 )(其中x1≠x2)进行计算.金题典例 光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标及入射光线的斜率.解:(方法1)设Q(0,y),则由题意得kQA=-kQB.∵kQA=(1"-" y)/2,kQB=(3"-" y)/4,∴(1"-" y)/2=-(3"-" y)/4.解得y=5/3,即点Q的坐标为 0,5/3 ,∴k入=kQA=(1"-" y)/2=-1/3.(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3), kAB'=(1"-" 3)/(2+4)=-1/3,由题意得,A、Q、B'三点共线.从而入射光线的斜率为kAQ=kAB'=-1/3.所以,有(1"-" y)/2=(1"-" 3)/(2+4),解得y=5/3,点Q的坐标为(0,5/3).

人教版高中数学选择性必修二变化率问题教学设计
导语在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识,定性的研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长” 是越来越慢的,“指数爆炸” 比“直线上升” 快得多,进一步的能否精确定量的刻画变化速度的快慢呢,下面我们就来研究这个问题。新知探究问题1 高台跳水运动员的速度高台跳水运动中,运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+4.8t+11.如何描述用运动员从起跳到入水的过程中运动的快慢程度呢?直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动的越来越慢,在下降阶段运动的越来越快,我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度v ?近似的描述它的运动状态。




