-

农业田园综合体发展情况调研报告
1、夯实基础,完善农业生态体系。一是集中连片开展高标准农田建设,提升生产基础条件。XXX田园综合体核心区占地4500亩,完成投资7049万元,对农田进行改造治理。XXX项目投资560万元,实施高标准农田2000亩。项目建成后,可有效改善农田基础设施条件,增加村民收入。二是实施新建园区道路及配套工程。XXX田园综合体路基、路面已全部完成施工,其他农业配套设施基本完成。XXXX项目新修道路3条1210米,拓宽1条726米,新建交通桥2座、拦河坝1座,过路管涵6座,进地管涵26座,提升园区内的通达条件。水电等基础保障得到升级改造,生产配套条件明显提升。三是加快土地流转,提升农业生产规模化、产业化水平。XXXX项目流转土地3000亩,发展小红星标准化生产基地,通过加快土地流转,实现土地、劳力、资金、技术、信息等生产要素的优化配置和组合,促进产业结构调整与优化。

对提升办公室综合协调服务能力的几点思考
当前存在的一些问题:一是文件传阅慢。一份文件由于常常需要多位领导、多个室局股阅知,往往就造成了文件传递时间长,文件传阅慢的问题。有时一份文件传阅结束时时间长达一个月,文件传阅效率严重低下;有时文件传到后面领导阅知时,事情都已经过去了,对工作的开展带来了不利影响。

幼儿园中班综合活动说课稿 有趣的萝卜
此活动选材来源于生活。我们都知道,萝卜是幼儿比较熟悉的蔬菜之一,在秋天这个丰收的季节,萝卜在农村随处可见,且取材方便。它的品种非常丰富,有白萝卜、胡萝卜等,其中大小不同、颜色不同、形状不同;它营养丰富,吃法繁多,可煮汤、可凉拌、可红烧、可腌着吃,有的还可生吃呢!民间还有“十月萝卜小人参”的美称。 然而幼儿虽然知道萝卜,但对萝卜的种类、用途、营养价值等还不太了解,在日常生活中经常发现幼儿不爱吃萝卜的现象。因此,有必要使幼儿形成对萝卜正确的认识,加深对萝卜的特征、用途等的理解,激发幼儿爱萝卜的情感。我认为此活动来源于生活,又能服务于幼儿的生活。就如《纲要》中所说,“既符合幼儿的现实需要,又有利于其长远发展;既贴近幼儿的生活,选择感兴趣的事物或问题,又有助于拓展幼儿的经验和视野”。

高校学工部(团委)2023年工作总结
一、学生工作(一)日常管理工作1.加强疫情期间学生管理,严格出入管理,专科生一般不允许外出,特殊情况(事假、病假等)需提交申请,经相关部门、学校领导批示后方可离校。落实在校生“日报告、零报告”制度和体温晨午检制度、因病缺勤追踪登记制度,及时收集异常健康信息并及时上报,组织各系做好学生核酸检测相关工作,确保应检尽检,不漏一人。2.加强学生住宿管理,积极管理中心组织宿管员、安保员多次召开专题会议,加大宿舍区巡查力度,增强工作人员责任意识,提高安全防范意识,同时,进一步落实辅导员进宿舍规定,强化宿舍夜间值班制度,协多方力量共同维护宿舍区安全、稳定。3.开展新生入学教育,组织新生军训、开学典礼等活动,加强学生理想信念教育、爱国爱校教育、安全稳定教育、校规校纪教育、国防教育等。4.积极探索“网络新媒体+高校思想政治”工作新模式,扩展思政网络空间,学工部及团委微信公众号已覆盖全体在校生,其中,学工部微平台设立了“国奖人物”、迎新指南等板块,宣扬榜样力量,强化爱国教育、营造积极向上的校园氛围。团委微平台设立了团团快讯、青年之声等板块,立足宣传、发声的功能定位,着力提升网络舆论引导的影响力、引领力。

人教A版高中数学必修一诱导公式教学设计(1)
一、复习回顾,温故知新1. 任意角三角函数的定义【答案】设角 它的终边与单位圆交于点 。那么(1) (2) 2.诱导公式一 ,其中, 。终边相同的角的同一三角函数值相等二、探索新知思考1:(1).终边相同的角的同一三角函数值有什么关系?【答案】相等(2).角 -α与α的终边 有何位置关系?【答案】终边关于x轴对称(3).角 与α的终边 有何位置关系?【答案】终边关于y轴对称(4).角 与α的终边 有何位置关系?【答案】终边关于原点对称思考2: 已知任意角α的终边与单位圆相交于点P(x, y),请同学们思考回答点P关于原点、x轴、y轴对称的三个点的坐标是什么?【答案】点P(x, y)关于原点对称点P1(-x, -y)点P(x, y)关于x轴对称点P2(x, -y) 点P(x, y)关于y轴对称点P3(-x, y)

人教A版高中数学必修一幂函数教学设计(2)
幂函数是在继一次函数、反比例函数、二次函数之后,又学习了单调性、最值、奇偶性的基础上,借助实例,总结出幂函数的概念,再借助图像研究幂函数的性质.课程目标1、理解幂函数的概念,会画幂函数y=x,y=x2,y=x3,y=x-1,y=x 的图象;2、结合这几个幂函数的图象,理解幂函数图象的变化情况和性质;3、通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.数学学科素养1.数学抽象:用数学语言表示函数幂函数;2.逻辑推理:常见幂函数的性质;3.数学运算:利用幂函数的概念求参数;4.数据分析:比较幂函数大小;5.数学建模:在具体问题情境中,运用数形结合思想,利用幂函数性质、图像特点解决实际问题。重点:常见幂函数的概念、图象和性质;难点:幂函数的单调性及比较两个幂值的大小.

人教A版高中数学必修一对数的运算教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.3.2节《对数的运算》。其核心是弄清楚对数的定义,掌握对数的运算性质,理解它的关键就是通过实例使学生认识对数式与指数式的关系,分析得出对数的概念及对数式与指数式的 互化,通过实例推导对数的运算性质。由于它还与后续很多内容,比如对数函数及其性质,这也是高考必考内容之一,所以在本学科有着很重要的地位。解决重点的关键是抓住对数的概念、并让学生掌握对数式与指数式的互化;通过实例推导对数的运算性质,让学生准确地运用对数运算性质进行运算,学会运用换底公式。培养学生数学运算、数学抽象、逻辑推理和数学建模的核心素养。1、理解对数的概念,能进行指数式与对数式的互化;2、了解常用对数与自然对数的意义,理解对数恒等式并能运用于有关对数计算。

人教A版高中数学必修一对数的运算教学设计(2)
学生已经学习了指数运算性质,有了这些知识作储备,教科书通过利用指数运算性质,推导对数的运算性质,再学习利用对数的运算性质化简求值。课程目标1、通过具体实例引入,推导对数的运算性质;2、熟练掌握对数的运算性质,学会化简,计算.数学学科素养1.数学抽象:对数的运算性质;2.逻辑推理:换底公式的推导;3.数学运算:对数运算性质的应用;4.数学建模:在熟悉的实际情景中,模仿学过的数学建模过程解决问题.重点:对数的运算性质,换底公式,对数恒等式及其应用;难点:正确使用对数的运算性质和换底公式.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入回顾指数性质:(1)aras=ar+s(a>0,r,s∈Q).(2)(ar)s= (a>0,r,s∈Q).(3)(ab)r= (a>0,b>0,r∈Q).那么对数有哪些性质?如 要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.

人教A版高中数学必修一对数的概念教学设计(2)
对数与指数是相通的,本节在已经学习指数的基础上通过实例总结归纳对数的概念,通过对数的性质和恒等式解决一些与对数有关的问题.课程目标1、理解对数的概念以及对数的基本性质;2、掌握对数式与指数式的相互转化;数学学科素养1.数学抽象:对数的概念;2.逻辑推理:推导对数性质;3.数学运算:用对数的基本性质与对数恒等式求值;4.数学建模:通过与指数式的比较,引出对数定义与性质.重点:对数式与指数式的互化以及对数性质;难点:推导对数性质.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入已知中国的人口数y和年头x满足关系 中,若知年头数则能算出相应的人口总数。反之,如果问“哪一年的人口数可达到18亿,20亿,30亿......”,该如何解决?要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.

人教A版高中数学必修一函数的概念教学设计(2)
函数在高中数学中占有很重要的比重,因而作为函数的第一节内容,主要从三个实例出发,引出函数的概念.从而就函数概念的分析判断函数,求定义域和函数值,再结合三要素判断函数相等.课程目标1.理解函数的定义、函数的定义域、值域及对应法则。2.掌握判定函数和函数相等的方法。3.学会求函数的定义域与函数值。数学学科素养1.数学抽象:通过教材中四个实例总结函数定义;2.逻辑推理:相等函数的判断;3.数学运算:求函数定义域和求函数值;4.数据分析:运用分离常数法和换元法求值域;5.数学建模:通过从实际问题中抽象概括出函数概念的活动,培养学生从“特殊到一般”的分析问题的能力,提高学生的抽象概括能力。重点:函数的概念,函数的三要素。难点:函数概念及符号y=f(x)的理解。

人教A版高中数学必修一任意角教学设计(1)
本节课选自《普通高中课程标准数学教科书-必修一》(人 教A版)第五章《三角函数》,本节课是第1课时,本节主要介绍推广角的概念,引入正角、负角、零角的定义,象限角的概念以及终边相同的角的表示法。树立运动变化的观点,并由此进一步理解推广后的角的概念。教学方法可以选用讨论法,通过实际问题,如时针与分针、体操等等都能形成角的流念,给学生以直观的印象,形成正角、负角、零角的概念,明确规定角的概念,通过具体问题让学生从不同角度理解终边相同的角,从特殊到一般归纳出终边相同的角的表示方法。A.了解任意角的概念;B.掌握正角、负角、零角及象限角的定义,理解任意角的概念;C.掌握终边相同的角的表示方法;D.会判断角所在的象限。 1.数学抽象:角的概念;2.逻辑推理:象限角的表示;3.数学运算:判断角所在象限;4.直观想象:从特殊到一般的数学思想方法;

人教A版高中数学必修一任意角教学设计(2)
学生在初中学习了 ~ ,但是现实生活中随处可见超出 ~ 范围的角.例如体操中有“前空翻转体 ”,且主动轮和被动轮的旋转方向不一致.因此为了准确描述这些现象,本节课主要就旋转度数和旋转方向对角的概念进行推广.课程目标1.了解任意角的概念.2.理解象限角的概念及终边相同的角的含义.3.掌握判断象限角及表示终边相同的角的方法.数学学科素养1.数学抽象:理解任意角的概念,能区分各类角;2.逻辑推理:求区域角;3.数学运算:会判断象限角及终边相同的角.重点:理解象限角的概念及终边相同的角的含义;难点:掌握判断象限角及表示终边相同的角的方法.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入初中对角的定义是:射线OA绕端点O按逆时针方向旋转一周回到起始位置,在这个过程中可以得到 ~ 范围内的角.但是现实生活中随处可见超出 ~ 范围的角.例如体操中有“前空翻转体 ”,且主动轮和被动轮的旋转方向不一致.

人教A版高中数学必修二简单随机抽样教学设计
知识探究(一):普查与抽查像人口普查这样,对每一个调查调查对象都进行调查的方法,称为全面调查(又称普查)。 在一个调查中,我们把调查对象的全体称为总体,组成总体的每一个调查对象称为个体。为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,每一个调查对象的相应指标作为个体。问题二:除了普查,还有其他的调查方法吗?由于人口普查需要花费巨大的财力、物力,因而不宜经常进行。为了及时掌握全国人口变动状况,我国每年还会进行一次人口变动情况的调查,根据抽取的居民情况来推断总体的人口变动情况。像这样,根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和判断的方法,称为抽样调查(或称抽查)。我们把从总体中抽取的那部分个体称为样本,样本中包含的个体数称为样本量。

人教A版高中数学必修一诱导公式教学设计(2)
本节主要内容是三角函数的诱导公式中的公式二至公式六,其推导过程中涉及到对称变换,充分体现对称变换思想在数学中的应用,在练习中加以应用,让学生进一步体会 的任意性;综合六组诱导公式总结出记忆诱导公式的口诀:“奇变偶不变,符号看象限”,了解从特殊到一般的数学思想的探究过程,培养学生用联系、变化的辩证唯物主义观点去分析问题的能力。诱导公式在三角函数化简、求值中具有非常重要的工具作用,要求学生能熟练的掌握和应用。课程目标1.借助单位圆,推导出正弦、余弦第二、三、四、五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题2.通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。

2017吉林中考语文真题及答案
说时迟,那时快,薛霸的棍恰举起来,只见松树背后雷鸣也似一声,那条铁禅杖飞将来,把这水火棍一隔,丢去九霄云外,跳出一个胖大和尚来,喝道:“洒家在林子里听你多时!”……两个公人看那和尚时,穿一领皂布直裰,跨一口戒刀,提起禅杖,抡起来打两个公人。林冲刚才让开眼看时,认得是鲁智深。

2017北京市中考语文真题及答案
风能就是地球表面大量空气流动所产生的动能。据估算,全球风能约为2.74×1012千瓦,其中可利用的风能约为2×1010千瓦,比地球上可开发利用的水能总量要大10倍。 目前,风力发电已经成为风能利用的主要形式。随着经济的高速增长和能源消耗的持续上升,煤炭、石油等常规能源日益枯竭,环境持续恶化。

2014北京市中考语文真题及答案
余幼时即嗜学。家贫,无从致书以观,每假借于藏书之家,手自笔录,计日以还。天大寒,砚冰坚,手指不可屈伸,弗之怠。录毕,走送之,不敢稍逾约。以是人多以书假余,余因得遍观群书。

2020北京市中考语文真题及答案
十年春,齐师伐我。公将战,曹刿请见。其乡人日:“肉食者谋之,又何间焉?”刿曰:“肉食者鄙,未能远谋。”乃入见。问:“何以战?”公曰:“衣食所安,弗敢专也,必以分人。”

2015北京市中考语文真题及答案
【甲】予观夫巴陵胜状,在洞庭一湖。衔远山,吞长江,浩浩汤汤,横无际涯;朝晖夕阳,气象万千。此则岳阳楼之大观也,前人之述备矣。然则北通巫峡,南极潇湘,迁客骚人,多会于此,览物之情,得无异乎?
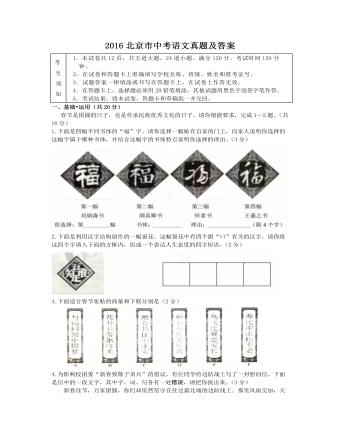
2016北京市中考语文真题及答案
京剧是流行全国的戏曲剧中之一。自清乾隆五十五年起,四大徽班陆续进京演出,他们相互影响,并接受昆区和秦腔的部分剧目、曲调、表演方法,又吸收了一些民间曲调,就是在这样的融合、演变和发展中京剧逐渐形成。在京剧发展的历程中,产生过许多优秀的演员。

