-

人教A版高中数学必修一诱导公式教学设计(2)
本节主要内容是三角函数的诱导公式中的公式二至公式六,其推导过程中涉及到对称变换,充分体现对称变换思想在数学中的应用,在练习中加以应用,让学生进一步体会 的任意性;综合六组诱导公式总结出记忆诱导公式的口诀:“奇变偶不变,符号看象限”,了解从特殊到一般的数学思想的探究过程,培养学生用联系、变化的辩证唯物主义观点去分析问题的能力。诱导公式在三角函数化简、求值中具有非常重要的工具作用,要求学生能熟练的掌握和应用。课程目标1.借助单位圆,推导出正弦、余弦第二、三、四、五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题2.通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。

人教版高中数学选修3排列与排列数教学设计
4.有8种不同的菜种,任选4种种在不同土质的4块地里,有 种不同的种法. 解析:将4块不同土质的地看作4个不同的位置,从8种不同的菜种中任选4种种在4块不同土质的地里,则本题即为从8个不同元素中任选4个元素的排列问题,所以不同的种法共有A_8^4 =8×7×6×5=1 680(种).答案:1 6805.用1、2、3、4、5、6、7这7个数字组成没有重复数字的四位数.(1)这些四位数中偶数有多少个?能被5整除的有多少个?(2)这些四位数中大于6 500的有多少个?解:(1)偶数的个位数只能是2、4、6,有A_3^1种排法,其他位上有A_6^3种排法,由分步乘法计数原理,知共有四位偶数A_3^1·A_6^3=360(个);能被5整除的数个位必须是5,故有A_6^3=120(个).(2)最高位上是7时大于6 500,有A_6^3种,最高位上是6时,百位上只能是7或5,故有2×A_5^2种.由分类加法计数原理知,这些四位数中大于6 500的共有A_6^3+2×A_5^2=160(个).

人教版高中数学选修3超几何分布教学设计
探究新知问题1:已知100件产品中有8件次品,现从中采用有放回方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.(1):采用有放回抽样,随机变量X服从二项分布吗?采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即X~B(4,0.08).(2):如果采用不放回抽样,抽取的4件产品中次品数X服从二项分布吗?若不服从,那么X的分布列是什么?不服从,根据古典概型求X的分布列.解:从100件产品中任取4件有 C_100^4 种不同的取法,从100件产品中任取4件,次品数X可能取0,1,2,3,4.恰有k件次品的取法有C_8^k C_92^(4-k)种.一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为P(X=k)=CkM Cn-kN-M CnN ,k=m,m+1,m+2,…,r.其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M},则称随机变量X服从超几何分布.

人教版高中数学选修3二项式定理教学设计
二项式定理形式上的特点(1)二项展开式有n+1项,而不是n项.(2)二项式系数都是C_n^k(k=0,1,2,…,n),它与二项展开式中某一项的系数不一定相等.(3)二项展开式中的二项式系数的和等于2n,即C_n^0+C_n^1+C_n^2+…+C_n^n=2n.(4)在排列方式上,按照字母a的降幂排列,从第一项起,次数由n次逐项减少1次直到0次,同时字母b按升幂排列,次数由0次逐项增加1次直到n次.1.判断(正确的打“√”,错误的打“×”)(1)(a+b)n展开式中共有n项. ( )(2)在公式中,交换a,b的顺序对各项没有影响. ( )(3)Cknan-kbk是(a+b)n展开式中的第k项. ( )(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )[解析] (1)× 因为(a+b)n展开式中共有n+1项.(2)× 因为二项式的第k+1项Cknan-kbk和(b+a)n的展开式的第k+1项Cknbn-kak是不同的,其中的a,b是不能随便交换的.(3)× 因为Cknan-kbk是(a+b)n展开式中的第k+1项.(4)√ 因为(a-b)n与(a+b)n的二项式展开式的二项式系数都是Crn.[答案] (1)× (2)× (3)× (4)√

人教版高中数学选修3全概率公式教学设计
2.某小组有20名射手,其中1,2,3,4级射手分别为2,6,9,3名.又若选1,2,3,4级射手参加比赛,则在比赛中射中目标的概率分别为0.85,0.64,0.45,0.32,今随机选一人参加比赛,则该小组比赛中射中目标的概率为________. 【解析】设B表示“该小组比赛中射中目标”,Ai(i=1,2,3,4)表示“选i级射手参加比赛”,则P(B)= P(Ai)P(B|Ai)= 2/20×0.85+ 6/20 ×0.64+ 9/20×0.45+ 3/20×0.32=0.527 5.答案:0.527 53.两批相同的产品各有12件和10件,每批产品中各有1件废品,现在先从第1批产品中任取1件放入第2批中,然后从第2批中任取1件,则取到废品的概率为________. 【解析】设A表示“取到废品”,B表示“从第1批中取到废品”,有P(B)= 112,P(A|B)= 2/11 ,P(A| )= 1/11所以P(A)=P(B)P(A|B)+P( )P(A| )4.有一批同一型号的产品,已知其中由一厂生产的占 30%, 二厂生产的占 50% , 三厂生产的占 20%, 又知这三个厂的产品次品率分别为2% , 1%, 1%,问从这批产品中任取一件是次品的概率是多少?

人教版高中数学选修3条件概率教学设计
(2)方法一:第一次取到一件不合格品,还剩下99件产品,其中有4件不合格品,95件合格品,于是第二次又取到不合格品的概率为4/99,由于这是一个条件概率,所以P(B|A)=4/99.方法二:根据条件概率的定义,先求出事件A,B同时发生的概率P(AB)=(C_5^2)/(C_100^2 )=1/495,所以P(B|A)=(P"(" AB")" )/(P"(" A")" )=(1/495)/(5/100)=4/99.6.在某次考试中,要从20道题中随机地抽出6道题,若考生至少答对其中的4道题即可通过;若至少答对其中5道题就获得优秀.已知某考生能答对其中10道题,并且知道他在这次考试中已经通过,求他获得优秀成绩的概率.解:设事件A为“该考生6道题全答对”,事件B为“该考生答对了其中5道题而另一道答错”,事件C为“该考生答对了其中4道题而另2道题答错”,事件D为“该考生在这次考试中通过”,事件E为“该考生在这次考试中获得优秀”,则A,B,C两两互斥,且D=A∪B∪C,E=A∪B,由古典概型的概率公式及加法公式可知P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)=(C_10^6)/(C_20^6 )+(C_10^5 C_10^1)/(C_20^6 )+(C_10^4 C_10^2)/(C_20^6 )=(12" " 180)/(C_20^6 ),P(E|D)=P(A∪B|D)=P(A|D)+P(B|D)=(P"(" A")" )/(P"(" D")" )+(P"(" B")" )/(P"(" D")" )=(210/(C_20^6 ))/((12" " 180)/(C_20^6 ))+((2" " 520)/(C_20^6 ))/((12" " 180)/(C_20^6 ))=13/58,即所求概率为13/58.

人教版高中数学选修3正态分布教学设计
3.某县农民月均收入服从N(500,202)的正态分布,则此县农民月均收入在500元到520元间人数的百分比约为 . 解析:因为月收入服从正态分布N(500,202),所以μ=500,σ=20,μ-σ=480,μ+σ=520.所以月均收入在[480,520]范围内的概率为0.683.由图像的对称性可知,此县农民月均收入在500到520元间人数的百分比约为34.15%.答案:34.15%4.某种零件的尺寸ξ(单位:cm)服从正态分布N(3,12),则不属于区间[1,5]这个尺寸范围的零件数约占总数的 . 解析:零件尺寸属于区间[μ-2σ,μ+2σ],即零件尺寸在[1,5]内取值的概率约为95.4%,故零件尺寸不属于区间[1,5]内的概率为1-95.4%=4.6%.答案:4.6%5. 设在一次数学考试中,某班学生的分数X~N(110,202),且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分及90分以上)的人数和130分以上的人数.解:μ=110,σ=20,P(X≥90)=P(X-110≥-20)=P(X-μ≥-σ),∵P(X-μσ)≈2P(X-μ130)=P(X-110>20)=P(X-μ>σ),∴P(X-μσ)≈0.683+2P(X-μ>σ)=1,∴P(X-μ>σ)=0.158 5,即P(X>130)=0.158 5.∴54×0.158 5≈9(人),即130分以上的人数约为9人.

人教版高中数学选修3组合与组合数教学设计
解析:因为减法和除法运算中交换两个数的位置对计算结果有影响,所以属于组合的有2个.答案:B2.若A_n^2=3C_(n"-" 1)^2,则n的值为( )A.4 B.5 C.6 D.7 解析:因为A_n^2=3C_(n"-" 1)^2,所以n(n-1)=(3"(" n"-" 1")(" n"-" 2")" )/2,解得n=6.故选C.答案:C 3.若集合A={a1,a2,a3,a4,a5},则集合A的子集中含有4个元素的子集共有 个. 解析:满足要求的子集中含有4个元素,由集合中元素的无序性,知其子集个数为C_5^4=5.答案:54.平面内有12个点,其中有4个点共线,此外再无任何3点共线,以这些点为顶点,可得多少个不同的三角形?解:(方法一)我们把从共线的4个点中取点的多少作为分类的标准:第1类,共线的4个点中有2个点作为三角形的顶点,共有C_4^2·C_8^1=48(个)不同的三角形;第2类,共线的4个点中有1个点作为三角形的顶点,共有C_4^1·C_8^2=112(个)不同的三角形;第3类,共线的4个点中没有点作为三角形的顶点,共有C_8^3=56(个)不同的三角形.由分类加法计数原理,不同的三角形共有48+112+56=216(个).(方法二 间接法)C_12^3-C_4^3=220-4=216(个).

在全市城市更新暨城镇老旧小区改造推进会上的讲话发言
二、肯定成绩,认清差距,勇于担当,破解难题,筑牢经济高质量发展的根基市委、市政府历来高度重视城市更新和城镇老旧小区改造工作,践行以人民为中心的发展思想,夯实责任,明确目标,不断加快城市更新、补齐城市发展短板、提升城市内涵品质。随着老旧小区改造、城市水系治理、综合管廊建设、人行道修缮、老旧建筑外立面改造等工作不断推进,城市水、电、路、气、绿化、美化、亮化等基础设施不断完善,城市居民的幸福感和满意度、城市品质品位和美誉度都有了大幅提升。

2017北京市中考语文真题及答案
风能就是地球表面大量空气流动所产生的动能。据估算,全球风能约为2.74×1012千瓦,其中可利用的风能约为2×1010千瓦,比地球上可开发利用的水能总量要大10倍。 目前,风力发电已经成为风能利用的主要形式。随着经济的高速增长和能源消耗的持续上升,煤炭、石油等常规能源日益枯竭,环境持续恶化。

2014北京市中考语文真题及答案
余幼时即嗜学。家贫,无从致书以观,每假借于藏书之家,手自笔录,计日以还。天大寒,砚冰坚,手指不可屈伸,弗之怠。录毕,走送之,不敢稍逾约。以是人多以书假余,余因得遍观群书。

2020北京市中考语文真题及答案
十年春,齐师伐我。公将战,曹刿请见。其乡人日:“肉食者谋之,又何间焉?”刿曰:“肉食者鄙,未能远谋。”乃入见。问:“何以战?”公曰:“衣食所安,弗敢专也,必以分人。”

2015北京市中考语文真题及答案
【甲】予观夫巴陵胜状,在洞庭一湖。衔远山,吞长江,浩浩汤汤,横无际涯;朝晖夕阳,气象万千。此则岳阳楼之大观也,前人之述备矣。然则北通巫峡,南极潇湘,迁客骚人,多会于此,览物之情,得无异乎?
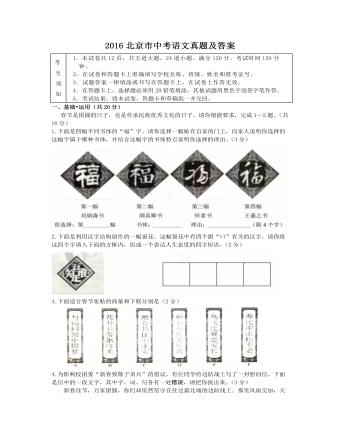
2016北京市中考语文真题及答案
京剧是流行全国的戏曲剧中之一。自清乾隆五十五年起,四大徽班陆续进京演出,他们相互影响,并接受昆区和秦腔的部分剧目、曲调、表演方法,又吸收了一些民间曲调,就是在这样的融合、演变和发展中京剧逐渐形成。在京剧发展的历程中,产生过许多优秀的演员。

2013北京市中考语文真题及答案
纪录片具有文献价值、文化意义和美学价值,2011年元旦,中央电视台纪录频道用中英文面向全球开播,它是我国首个覆盖国内外的纪录片专业频道。

2012北京市中考语文真题及答案
当代大画家李苦禅撒手人寰驾鹤西游的时候,我的老师许麟庐正在山东旅行。许老听到噩耗,立即登车,直奔北京。到了苦禅灵堂,满头白发的老人,长跪不起,恸哭不止。他和苦老,同是齐白石大师的弟子,手足之情,比一奶同胞还亲。

2011北京市中考语文真题及答案
过去,公交车五六分钟来一辆,现在一二分钟来一辆,方便多了。有的乘客说,现在坐公交上班比开私家车还快呢,很多时候我们都坐公交车了。

简约市场渠道应届生单页简历
20xx.09-20xx.06 校职业发展协会 担任:组织部长l 走访了近200个寝室,招揽了新会员300多名;l 总结协会为学员提供的利益,通过印制传单、海报、横幅、设摊答疑、宿舍楼走访等方式宣传;l 多次举办30人左右的宣讲座谈会,向到会者推介协会。l 曾多次参与各项活动的策划工作,担任执行方案的策划者以及活动发起人,具备文案功底和策划思维;l 向校内外各大商家拉取活动费用及物资赞助,进行商业沟通并撰写活动及商家宣传方案提供给商家;l 做好活动前期的对外宣传工作,保证活动现场的良好执行及把握好活动期间穿插商家宣传的时间点。

大班数学《去超市购物》说课稿
《纲要》指出:幼儿的发展是在与周围环境的相互作用中实现的,良好的教育环境对幼儿的身心发展具有积极的促进作用,应充分利用社区资源,拓展幼儿生活和学习的空间,借孩子感兴趣的事物,充分挖掘其潜在的、有利于孩子身心和谐发展的教育价值。超市是幼儿在日常生活中最熟悉的场所之一,超市里各种各样的物品吸引着幼儿。为此,我们选择了幼儿感兴趣的题材--“超市”开展主题活动。幼儿园数学是一门系统性、逻辑性很强的学科,有着自身的特点和规律,新《纲要》提出“数学教育必须要让幼儿能从生活和游戏中感受事物的数量关系并体验到数学的重要和有趣;教师要引导幼儿对周围环境中数、量、形、时间和空间等现象产生兴趣,建构初步的数概念,并学习用简单的数学方法解决生活和游戏中某些简单的问题。”由此可见生活化、游戏化已经成为构建数学课程最基本的原则。在对教材和本班幼儿的学习情况有一定了解后,我制定出本次活动目标:1、通过购物,学习5以内的加减运算;2、初步了解加减法算式所表达的实际意义。

大班语言《野猫的城市》说课稿
大班幼儿处于5、6岁左右,语言发展还是稍微欠缺,而且过不了多久就得进入学前班或者小学阶段。所以,这个阶段不仅是语言发展的生理关键期,也是知识奠基的重要阶段。他们比小班、中班幼儿更主动求知,但知识经验大都是根据自己的好奇与无数的巧合而获得的,都是很零碎的。除此之外,在语言表达上还不是很规范,特别是普通话方面才启蒙不久。理论上说,<4岁的幼儿重在感知语言能力;4-5岁重在感知和理解词义;5-6岁重在培养讲述。所以,通过这次语言活动,要根据大班幼儿在语言方面的缺失、幼儿需要达到的语言目标,建立一个民主、和谐的师生关系,给幼儿一个较为轻松的语言环境,培养幼儿对语言的表述能力与思维能力,能够有条理地讲述自己的观点,并且能在老师引导下,有意识的注意字音的准确性,尽量用标准的普通话规范自己。并借助作品来认识周围世界(即作品中的城市)

