-
北师大初中数学九年级上册概率与游戏的综合运用2教案
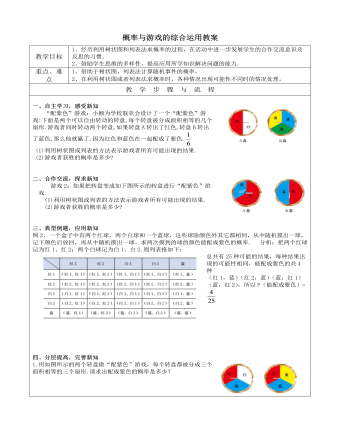
三、典型例题,应用新知例2、一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率. 分析:把两个红球记为红1、红2;两个白球记为白1、白2.则列表格如下:总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以P(能配成紫色)= 四、分层提高,完善新知1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 五、课堂小结,回顾新知1. 利用树状图和列表法求概率时应注意什么?2. 你还有哪些收获和疑惑?

北师大初中数学九年级上册反比例函数的图象2教案
观察 和 的图象,它们有什么相同点和不同点?学生小组讨论,弄清上述两个图象的异同点。交流讨论反比 例函数图象是中心对称图形吗?如果是,请找出对称中心.反比例函数图象是轴对称图形吗?如果是,请指出它的对称轴.二、随堂练习课本随堂练习 [探索与交流]对于函数 , 两支曲线分别位于哪个象限内?对于函数 ,两支曲线又分别位于哪个象限内?怎样区别这两个函数的图象。学生分四人小组全班探索。 三、课堂总结在进行函数的列表,描点作图的活动中,就已经渗透了反比例函数图象的特征,因此在作图象的过程中,大家要进行积极的探索 。另外,(1)反比例函数的图象是非线性的,它的图象是双曲线;(2)反比例 函数y= 的图像,当k>0时,它的图像位于一、三象限内,当k<0时,它的图像位于二、四象限内;(3)反比例函数既是中心对称图形,又是轴对称图形。

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的判定1教案
∵EG⊥FH,∴∠BOE+∠BOH=90°,∴∠COH=∠BOE,∴△CHO≌△BEO,∴OE=OH.同理可证:OE=OF=OG,∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO,即EG=HF,∴四边形EFGH为正方形.方法总结:对角线互相垂直平分且相等的四边形是正方形.探究点二:正方形、菱形、矩形与平行四边形之间的关系填空:(1)对角线________________的四边形是矩形;(2)对角线____________的平行四边形是矩形;(3)对角线__________的平行四边形是正方形;(4)对角线________________的矩形是正方形;(5)对角线________________的菱形是正方形.解:(1)相等且互相平分(2)相等(3)垂直且相等(4)垂直(5)相等方法总结:从对角线上分析特殊四边形之间的关系应充分考虑特殊四边形的性质与判别,防止混淆.菱形、矩形、正方形都是平行四边形,且是特殊的平行四边形,特殊之处在于:矩形是有一个角为直角的平行四边形;菱形是有一组邻边相等的平行四边形;而正方形是兼具两者特性的更特殊的平行四边形,它既是矩形,又是菱形.

北师大初中数学九年级上册简单图形的三视图2教案
教学目标:1.经历由实物抽象出几何体的过程,进一步发展空间观念。2.会画圆柱、圆锥、球的三视图,体会这几种几何体与其视图之间的相互转化。3.会根据三视图描述原几何体。教学重点:掌握部分几何体的三视图的画法,能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法教学过程设计一、实物观察、空间想像设置:学生利用准备好的大小相同的正方形方块,搭建一个立体图形,让同学们画出三视图。而后,再要求学生利用手中12块正方形的方块实物,搭建2个立体图形,并画出它们的三视图。学生分小组合作交流、观察、作图。议一议1.图5-14中物体的形状分别可以看成什么样的几何体?从正面、侧面、上面看这些几何体,它们的形状各是什么样的?2.在图5-15中找出图5-14中各物体的主视图。3.图5-14中各物体的左视图是什么?俯视图呢?

北师大初中数学九年级上册一元二次方程的解及其估算1教案
方法总结:(1)利用列表法估算一元二次方程根的取值范围的步骤是:首先列表,利用未知数的取值,根据一元二次方程的一般形式ax2+bx+c=0(a,b,c为常数,a≠0)分别计算ax2+bx+c的值,在表中找到使ax2+bx+c可能等于0的未知数的大致取值范围,然后再进一步在这个范围内取值,逐步缩小范围,直到所要求的精确度为止.(2)在估计一元二次方程根的取值范围时,当ax2+bx+c(a≠0)的值由正变负或由负变正时,x的取值范围很重要,因为只有在这个范围内,才能存在使ax2+bx+c=0成立的x的值,即方程的根.三、板书设计一元二次方程的解的估算,采用“夹逼法”:(1)先根据实际问题确定其解的大致范围;(2)再通过列表,具体计算,进行两边“夹逼”,逐步获得其近似解.“估算”在求解实际生活中一些较为复杂的方程时应用广泛.在本节课中让学生体会用“夹逼”的思想解决一元二次方程的解或近似解的方法.教学设计上,强调自主学习,注重合作交流,在探究过程中获得数学活动的经验,提高探究、发现和创新的能力.

北师大初中数学九年级上册线段的比和成比例线段1教案
故线段d的长度为94cm.方法总结:利用比例线段关系求线段长度的方法:根据线段的关系写出比例式,并把它作为相等关系构造关于要求线段的方程,解方程即可求出线段的长.已知三条线段长分别为1cm,2cm,2cm,请你再给出一条线段,使得它的长与前面三条线段的长能够组成一个比例式.解析:因为本题中没有明确告知是求1,2,2的第四比例项,因此所添加的线段长可能是前三个数的第四比例项,也可能不是前三个数的第四比例项,因此应进行分类讨论.解:若x:1=2:2,则x=22;若1:x=2:2,则x=2;若1:2=x:2,则x=2;若1:2=2:x,则x=22.所以所添加的线段的长有三种可能,可以是22cm,2cm,或22cm.方法总结:若使四个数成比例,则应满足其中两个数的比等于另外两个数的比,也可转化为其中两个数的乘积恰好等于另外两个数的乘积.

北师大初中数学九年级上册相似三角形的周长和面积之比2教案
●教学目标(一)教学知识点1.相似三角形的周长比,面积比与相似比的关系.2. 相似三角形的周长比,面积比在实际中的应用.(二)能 力训练要求1.经历探索相似三角形的 性质的过程,培养学生的探索能力.2.利用相似三角形的性质解决实际问题训练学生的运用能力.(三)情 感与价值观要求1.学 生通过交流、归纳,总结相似三角形的周长比、面积比与相似比的关系,体会知识迁移、温故知新的好处.2.运用相似多边形的周长比,面积比解决实际问题,增强学生对知识的应用意识.●教学重点1.相似三角形的周长比、面积比与相似比关系的推导.2.运用相似三角形的比例关系解决实际问题.●教学难点相似三角形周长比、面积比与相似比的关系的推导及运用.●教学方法引导启发式通过温故知新,知识迁移,引导学生发现新的结论,通过比较、分析,应用获得的知识达到理解并掌握的 目的.●教具准备投影片两张第一张:(记作§4.7.2 A)第二张:(记作§4.7.2 B)

北师大初中数学九年级上册一元二次方程的解及其估算2教案
(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业

北师大初中数学九年级上册相似三角形的周长和面积之比1教案
解:∵CF平分∠ACB,DC=AC,∴CF是△ACD的中线,即F是AD的中点.∵点E是AB的中点,∴EF∥BD,且EFBD=12.∴∠B=∠AEF,∠ADB=∠AFE,∴△AEF∽△ABD.∴S△AEFS△ABD=(12)2=14.∵S△AEF=S△ABD-S四边形BDFE=S△ABD-6,∴S△ABD-6S△ABD=14.∴S△ABD=8,即△ABD的面积为8.易错提醒:在运用“相似三角形的面积比等于相似比的平方”这一性质时,同样要注意是对应三角形的面积比,在本题中不要犯由EF:BD=1:2得S△AEF:S△ABD=1:2,或S△AEF:S四边形BDFE=1:2之类的错误.三、板书设计相似三角形的周长和面积之比:相似三角形的周长比等于相似比,面积比等于相似比的平方.经历相似三角形的性质的探索过程,培养学生的探索能力.通过交流、归纳,总结相似三角形的周长比、面积比与相似比的关系,体验化归思想.运用相似多边形的周长比,面积比解决实际问题,训练学生的运用能力,增强学生对知识的应用意识.

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的判定1教案
∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO,即EG=HF,∴四边形EFGH为正方形.方法总结:对角线互相垂直平分且相等的四边形是正方形.探究点二:正方形、菱形、矩形与平行四边形之间的关系填空:(1)对角线________________的四边形是矩形;(2)对角线____________的平行四边形是矩形;(3)对角线__________的平行四边形是正方形;(4)对角线________________的矩形是正方形;(5)对角线________________的菱形是正方形.解:(1)相等且互相平分(2)相等(3)垂直且相等(4)垂直(5)相等方法总结:从对角线上分析特殊四边形之间的关系应充分考虑特殊四边形的性质与判别,防止混淆.菱形、矩形、正方形都是平行四边形,且是特殊的平行四边形,特殊之处在于:矩形是有一个角为直角的平行四边形;菱形是有一组邻边相等的平行四边形;而正方形是兼具两者特性的更特殊的平行四边形,它既是矩形,又是菱形.
小学美术人教版二年级上册《第1课流动的颜色》教案说课稿
同学们在此之前是否有接触过颜料色彩?利用颜料色彩我们可以混合调出新的色彩吗?我们先进行一个小游戏,只提供三种颜色:红,蓝,绿,请三位学生上台进行调色,调色完后告诉大家自己发现了什么及是如何发现,游戏结束后我们进行交流与分享。游戏结束后进入我们新课程:流动的颜色 。

小学美术人教版一年级上册《第20课美丽的植物和动物》教案说课稿
2、懂得要爱护动植物,对破坏植物、残杀动物的行为表示气愤,在日常生活中能自觉做到爱护动植物,不做破坏动植物生态环境的事,积极参加保护动植物的公益活动。活动重点:感受动植物的生命现象,懂得爱护动植物。

小学美术人教版一年级上册《第12课我做的“文具”》教案说课稿
教学目标:1、在仔细观察常用文具的基础上,启发学生设计造型新颖、色彩鲜艳的各种常用文具。2、引导学生运用橡皮泥表现各种文具的形象,提高学生立体表现能力。教学重点:打开学生积极、丰富的创造性思维,引发对文具造型的兴趣。

人音版小学音乐四年级上阳光牵着我的手说课稿
一 、 根据课标要求,结合学生的实际,本课的设计理念是:本课以聆听《阳光下的孩子》作为导入,本课新授的内容是演唱少儿合唱曲《阳光牵着我的手》教学中以歌曲的情绪变化为主线展开一系列的听、唱、奏、创的活动在学习的过程中以学生对歌曲的初步演唱为主。最后的归纳总结环节让学生观看校园生活花絮背景音乐为《阳光牵着我的手》让学生在重温美好的校园时光同时考虑 如何做一个快乐的团结友爱的阳光少年既是对整堂课的一个提炼也体现了音乐课是生命快乐成长的摇篮。二 、 学情分析:农村小学中段的孩子在对音乐的感受和表现能力方面,能用自己的声音对它们进行模仿。能听辨不同情绪的音乐。基本掌握基础识读乐谱知识的能力,在课堂上能够看谱吹奏口琴,但在听辨单音及旋律音程方面还是有所欠缺,而且大部分同学缺乏初步的合唱经验,因此合唱教学上多采用律动、音乐游戏、歌唱表演等活动以及与 他人进行合作演唱二声部。以逐步增强孩子的合唱能力。

人音版小学音乐五年级上册雪花带来冬天的梦说课稿
(三)实践操作,表现歌曲。课标中指出,“表现是实践性很强的音乐学习领域,是学习音乐的基础性内容,是培养学生音乐表现能力和审美能力的重要途径。”再加上对于这个年龄段的学生来讲,他们特别喜欢表现自己,所以,我充分发挥集体的力量,设计“小小音乐家”的教学环节,让同学们在小组中合作学习,采用不同形式演唱、用打击乐器伴奏、歌舞表演等形式将唱、奏结合,唱、演结合,巩固学生对歌曲的学习,体验合作学习的快乐,养成学生共同参与的群体意识和相互尊重的合作精神和实践能力,这也更体现了课标中音乐课程价值所提出的要培养学生的“社会交往价值”。(四)拓展延伸,创编歌曲。课标中的“文化传承价值”中明确提出:“要让孩子们通过学习世界上其他国家和民族的的音乐文化,拓宽他们的审美视野,认识世界各民族音乐文化的丰富性和多样性,增进对不同文化的理解、尊重和热爱。”

人教部编版道德与法制三年级上册做学习的主人说课稿
4.这种合理安排时间的方法不仅仅适用于星期天,寒暑假的时候也可以用这种方法合理安排我们的时间。 三、好经验共分享(提前布置孩子回家搜集,用一句话写在纸上)1.要想成为真正的学习的主人,除了合理安排时间,还要掌 握一定的学习方法,课前老师让同学们把自己的学习方法写在了苹果卡片上,请同学们拿出这张卡片,PPT 出示交流要求:( 1)请同学们在小组内交流汇报你的学习方法。 ( 2)选 出一个最好的方法来汇报。 ( 3)将剩下的学习方法粘到绿色 的卡纸上。2.小组汇报交流课前整理在苹果卡片上的学习方法。 3.师补充学习方法,分别出示23 页四幅图。4.学习的方法有很多种,但适合自己的方法才是最好的方法。四、总结通过这节课的学习,我们懂得了要合理地安排时间,并且了解了更多的学习方法,今天老师就把这棵苹果树送给你们,课后的时候老师建议每个人都到苹果树前看一看你最喜欢 哪种学习方法,并且把这种方法运用到我们的学习中,老师 相信你们都会成为真正的学习的主人。

人音版小学音乐二年级上册快乐的音乐会说课稿
新课标中鼓励音乐创造,注重个性发展,教师应为学生提供发展个性的可能和空间。在这一环节中我以这样一句话:“嘘,别出声,我好像听到谁在叫我,引出小鸡,小鸭加入到我们都行列中来”导入。现在,能不能像老师一样,把这些小动物的声音编成歌词,创作出一首新的主题曲?谁来试试?”学生创编好歌词说:“小朋友们让我们,随着欢快的音乐唱起来、跳起来吧!”来举办一场快乐的音乐会。五、说板书根据本课的教学目标和教学重难点我的板书是这样设计的。板书课题引起学生注意,让学生知道本节课的教学内容;板书难点是为了达到突破难点的目的。六、说反思本课我以“快乐”为主线,贯穿全课。在课堂上体现了以教师为主导,学生为主线的教学理念,实现了合作探究式的学习方法。回顾整个教学环节,在拓展创编这一环节中,由于时间有限,我把学生局限于我预设的几种动物和乐器上,对学生的想象力有些限制。今后,我将力所能及的做到符合学生实际来设计教学。

人音版小学音乐二年级上册跳圆舞曲的小猫说课稿
教学过程一、新课导入二、完整聆听1.初听师:晚会的主角是一只可爱的?2.课题:跳圆舞曲的小猫3.学生自由模拟小猫的叫声。4.再听全曲,画图形谱。师:观察图形谱,音乐有几部分组成?三、聆听A段1. 初听,找出模拟小猫叫声的音色。(集体聆听、律动)2. 再次聆听,个体检测3. 学唱A段主体旋律。(老师范唱主体旋律)4. 集体聆听并随音乐律动。5. 集体检测师:刚才唱的主题句放到音乐中你们能找到吗?如果找到了就跟着唱一唱。四、聆听第二乐段1. 初听师:它和第一乐段有联系吗?(找出相同和不同的地方)2. 复听师:速度、情绪和第一乐段比较起来有何不同?五、聆听B乐段1. 初听(教师随音乐律动)2. 复听,隋老师再次划图形谱。3. 师生用木鱼合作演奏。4. 小组合作表演。六、聆听第四乐段1. 初听师:和前面哪段音乐相似?2. 复听师:不同之处在哪?七、完整聆听学生和老师一起律动。