-
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
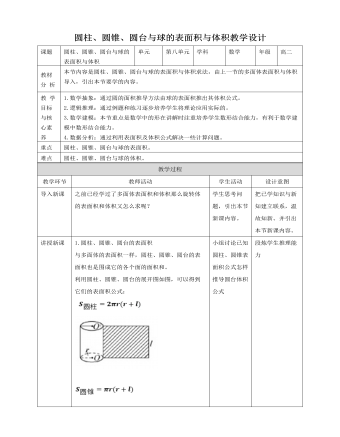
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
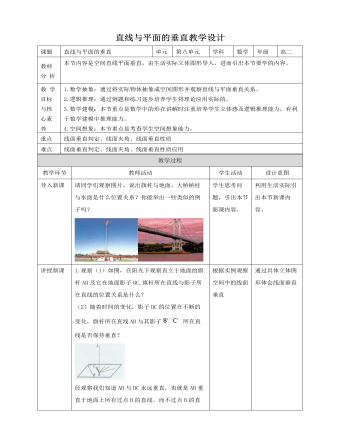
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

疫情开学语文教学的工作计划
1. 监管力度不一,学习效率参差。 线上学习,有部分家长很重视,为孩子提供了安静的学习环境,部分学生也很自律,能按时听课、积极思考、完成各项课内课外练习。但不排除存在家长无条件提供好的学习环境,学生缺乏自控能力的现象。我校生源一大部分是新居民子女,线上教学的中后期,学生家长绝大部分外出务工,学生的学习几乎处于“放任自流”的状态。孩子缺少大人的监督,不自觉更体现无疑,上课不专心,不记笔记,甚至不上课的也都存在,更别说语文的口头朗读、背诵作业和笔头的听写作业等的落实了。学生上课的参与率不保障,学校效率也参差不齐,两级分化明显。

2022年辽宁省营口市中考语文真题(解析版)
十年春,齐师伐我。公将战,曹刿请见。其乡人曰:“肉食者谋之,又何间焉?”刿曰:“肉食者鄙,未能远谋。”乃入见。问:“何以战?”公曰:“衣食所安,弗敢专也,必以分人。”对曰:“小惠未遍,民弗从也。”公曰:“牺牲玉帛,弗敢加也,必以信。”对曰:“小信未孚,神弗福也。”公曰:“小大之狱,虽不能察,必以情。”对日:“忠之属也。可以一战。战则请从。”

2022年山东省滨州市中考语文真题(原卷版)
阅读下面唐诗,完成下面小题。漫成一首杜甫江月去人只数尺,风灯①照夜欲三更。沙头宿鹭联拳②静,船尾跳鱼拨刺③鸣。【注释】①风灯:船中桅杆上挂着的灯,有纸罩能避风。②联拳:指夜宿的白鹭屈曲着身子,三五成群团聚在沙滩上。拳,屈曲。③拨刺:拟声词,指鱼在水里跳动发出的声音。11. 这首诗通过“_____________”“风灯”“宿鹭”“_________________”等意象,描绘出一幅恬淡平和的江上月夜图。

2022年辽宁省营口市中考语文真题(原卷版)
(二)(4分)阅读下面诗歌,完成下面小题。瀑布联句李忱千岩万壑不辞劳,远看方知出处高。溪涧焉能留得住,终归大海作波涛。14. 首句运用了什么手法?有什么表达效果?15. 请简要分析最后两句寄寓了作者怎样的情怀?

广西贺州市2021年中考语文试题(原卷版)
先帝知臣谨慎,故临崩寄臣以大事也。受命以来,夙夜忧叹,恐托付不效,以伤先帝之明;故五月渡泸,深入不毛。今南方已定,兵甲已足,当奖率三军,北定中原,庶竭驽钝,攘除奸凶,兴复汉室,还于旧都。此臣所以报先帝而忠陛下之职分也。至于斟酌损益,进尽忠言,则攸之、祎、允之任也。

广西百色市2021年中考语文试题(解析版)
历史老师无奈地说过:“有次我让大家整理近代史的笔记,别人都是两三张纸就搞定了,你知道崔安然写了多少吗?56页!唉……”数学老师总结道:“崔安然啊……就是单纯的脑子笨。”我还听隔壁班的王梦茹同学说,她俩是发小,上学时崔安然在学习方面就认真而吃力,效果不理想。

广西百色市2021年中考语文试题(原卷版)
我开始格外关注这个笨小孩:凌乱的头发,额头上此消彼长的痘痘,瘦小的肩膀……明明是单薄的小姑娘,身体里却像是有使不完的能量,面对大大小小的挫折时她波澜不惊、一往无前地继续努力,偶有一丝焦虑掠过,也稍纵即逝。我不知道那压力如山的一天又一天,崔安然究竟是怎么扛下来的……这一切,都令人心疼。

广西玉林市2021年中考语文真题(解析版)
之后,阿根廷决赛战胜联邦德国,获得了1986年世界杯冠军,马拉多纳凭借5个进球、5个助攻获得金球奖。1990年,马拉多纳带领阿根廷队获得世界杯亚军。1994年,马拉多纳带领阿根廷队再度冲击世界杯,结果因药检阳性禁赛,这导致阿根廷队军心大乱,止步八分之一决赛。1997年10月,马拉多纳宣布退役。

广西梧州市2021年中考语文试题(原卷版)
哲人有言,英雄的业绩、他们的言论,就是那个时代的精华。的确,英雄是一个民族的“凝结核”。如杨靖宇所言,“革命就像火一样,任凭大雪封山,鸟兽藏迹,只要我们有火种,就能驱赶严寒,带来光明和温暖。”英雄就是这革命的火种,没有英雄的引领,个体的力量就难以凝聚;缺少先锋的领路,前行的方向将难以看清。马克思因此感慨,“每一个社会时代都需要有自己的伟大人物”。

广西桂林市2021年中考语文试题(解析版)
山不在高,有仙则名。水不在深,有龙则灵。斯是陋室,惟吾德馨。苔痕上阶绿,草色入帘青。谈笑有鸿儒,往来无白丁。可以调素琴,阅金经。无丝竹之乱耳,无案牍之劳形。南阳诸葛庐,西蜀子云亭。孔子云:何陋之有?

2022年湖南省怀化市中考语文真题(解析版)
【海外网2月21日电】2月20日,北京冬奥会正式闭幕,这届冬奥会为世界留下了独具特色的中国记忆,收获了众多好评,各国运动员持续发文为北京冬奥会点赞。“感谢、祝福”成了高频词。

2022年湖北省宜昌市中考语文真题(原卷版)
倘若意犹未尽,试看杨万里的《郡中送春盘》:“饼如茧纸不可风,菜如缥茸劣可缝。韭芽卷黄苣舒紫,芦服削冰寒脱齿。”白如茧纸的是春饼,吃的时候,从春盘里夹取菜蔬各一小箸,卷为细简状,这便是咬春饼。

2022年浙江省绍兴市中考语文真题(解析版)
“无废城市”,是以创新、协调、绿色、开放、共享的新发展理念为引领,通过推动形成绿色发展方式和生活方式,持续推进固体废物源头减量和资源化利用,最大限度减少填埋量,将固体废物环境影响降至最低的城市发展模式。2017年,中国工程院院士杜祥豌在国内首次牵头提出创建“无废城市”及“无废社会”的建议。
2022年浙江省温州市中考语文真题(解析版)
桃花峪是黄河中下游分界线,把桥建在这里自有讲究。我个人的选择原因,就实用层面来讲,自是离老家更近,却也有非实用层面:是它的外形更时尚更壮观,名字我也格外钟爱:桃花峪——黄河——大桥,既明艳又铿锵,既坚固又绵长,不是么?

