-

江苏省徐州市2015年中考语文真题试题(无答案)
(1)人类几千年的历史,各种信仰和主义可谓多矣,虽然我们并不一定都要皈依某种宗教,但是每一个人的内心中都应该有指引自己前行的信仰。今天,当物质的匮乏不再困扰我们时,心灵的成长便成为生命的第一要务。每一个人的内心中都应该有一个自己的“上帝”,而真正的信仰不仅是一种理论,是一种实践,一种内在生命的实际体验,更是精神的支持和动力。如果有一种信仰能让全世界不同国家、不同民族毫无争议地共同信守的话,那就是阅读了。在历史长河中,有关宗教的庙宇与雕像在风雨中颓毁坍塌,而经典之籍则与世长存。文字是人类文明最上乘的结晶,它如此精微,如此难以把握,如此透彻,又如此无孔不入,穿透人的感知。人类的文明以文字的脉络一代又一代地传承下来,因此,在某种意义上,阅读已经超越了人类历史上的任何宗教,既没有时空界限,也没有地域之分,让生活在不同时代、不同国度,说着不同语言的人们,在阅读中共生。

浙江省杭州市2017年中考语文真题试题(含答案)
已近年关,隐藏在大山褶皱里的小县城年味渐浓。火车的汽笛声频繁地响起。一条悠长的巷道里藏着几户人家。一座陈旧的小四合院里传来清脆的电话铃声。 妈,再过一两个小时我们就到家了,晚饭回家吃,一年没吃到您做的饭了,呵呵。 你这孩子,咋突然就改主意了?不早讲,也好让妈提前高兴着,刚才还和苗苗念叨呢,苗苗一直想去看你们呢。 不是想给您个惊喜吗,呵呵。

甘肃省天水市2016年中考语文真题试题(含答案)
前段时间,因一场暴雨,一个亲戚让我帮他接小孩。放学时节,某小学门前的广场上,车声鼎沸,喇叭声震耳欲聋。一眼望去,雨雾之中处处是小车,挤满了整个广场,都是来接孩子的。也有家长骑着摩托车、电瓶车、自行车,他们让孩子穿着雨披坐在身后,穿行于停在广场的汽车中间。

广西贺州市2016年中考语文真题试题(含答案)
莫振高,2015年度感动中国人物。他是广西都安瑶族自治县高级中学校长,他将“让瑶乡儿女走向世界”作为自己的座右铭。任教30多年来,莫振高跑遍每一位贫困生的家,用自己微薄的工资资助近300名贫困生顺利进入大学,先后筹集3000多万无善款资助1.8万名贫困生圆了大学梦。因积劳成疾,莫振高于2015年3月9日突发心脏病去世,享年58岁。

北京市2016年中考语文真题试题(含答案)
京剧是流行全国的戏曲剧中之一。自清乾隆五十五年起,四大徽班陆续进京演出,他们相互影响,并接受昆区和秦腔的部分剧目、曲调、表演方法,又吸收了一些民间曲调,就是在这样的融合、演变和发展中京剧逐渐形成。在京剧发展的历程中,产生过许多优秀的演员。

湖北省鄂州市2016年中考语文真题试题(含答案)
【乙】小石城山记自西山道口径北,逾黄茅岭①而下,有二道。其一西出,寻之无所得;其一少北而东,不过四十丈,土断而川分,有积石横当其垠②。其上,为睥睨梁之形③;其旁,出堡坞④,有若门焉。窥之正黑,投以小石,洞然有水声,其响之激越,良久乃已。环之可上,望甚远。无土壤而生嘉树美箭⑤,益奇而坚,其疏数偃仰,类智者所施设也。噫!吾疑造物者之有无久矣。及是,愈以为诚有。又怪其不为之于中州⑥,而列是夷狄⑦,更千百年不得一售其伎⑧,是固劳而无用。神者傥不宜如是,则其果无乎;或曰:“以慰夫贤而辱于此者。”或曰:“其气之灵不为伟人而独为是物故楚之南少人而多石⑨。”是二者,余未信之。

2019年安徽中考语文试题及参考答案
近几十年来,数字计算机已经改变了几乎所有经济部门的工作,我们正处于一更迅速转变的开始阶段,但关于机器学习对劳动力和经济的具体影响的认识并未确定。目前一些工作的一部分适合机器学习,而其他部分还不适合。因而,机器学习对劳动力和经济的影响还是有限的,还没有像有些人宣称的那样——会迎来“工作的终结”。

重庆市2016年中考语文真题试题(B卷,含答案)
夜深了,广场上游客稀疏,灯火慵懒,小吴拖着疲惫的身躯,追上了20路公交车。公交车从我跟前一闪而过时,我看见小吴抓着吊环,挤在一群人中间,眼里满是恋恋不舍。

2021年安徽中考语文试题及参考答案
落地已是半夜,打开手机,收到太太发来的视频,录的是她跟儿子的对话。先从那幅画的构思说起。为什么把自己画成一个胖子?想让自己吃得壮壮的,好打篮球。为什么把衣服都涂成黄色?喜欢黄颜色啊。

四川省宜宾市2016年中考语文真题试题(含答案)
川菜发源于我国古代的巴国和蜀国。它经历了从春秋至两晋的雏形期,隋唐到五代的较大发展,两宋出川传至各地,至清末民初形成菜系四个阶段。其后,从辛亥革命到抗日战争,中国烹任各派交融,使川菜更加丰富。

2020年安徽中考语文试题及参考答案
儿童在教育过程中的成长,一定意义上就是在重演人类的发展史。我们的祖先通过劳动实现了人类文明的提升,由此我们每个人,特别是我们在儿童阶段的成长,都离不开劳动环节的淬炼。

2017年安徽中考语文试题及参考答案
在村庄的记忆里,几乎任何时间、任何角落都能见到扁担的身影。挑粪、挑种子、挑谷子、挑土豆、挑橘子……农人在土地上的所有倾注与收获,都与扁担密不可分。扁担就是农人的精神脊梁,让他们挑起一个家庭重担的同时,也挑起了一个村庄沉重的历史与殷殷期盼。

2013年安徽中考语文试题及参考答案
“稻花香里说丰年,听取蛙声一片。”你们只听见辛弃疾先生在宋朝这样说,我可是踏着蛙歌一路走过来的。我童年的摇篮,少说也被几百万只青蛙摇动过。我妈说:一到夏天外婆就不摇你了,远远近近的青蛙们都卖力地晃悠你,他们的摇篮歌,比你外婆唱的还好听哩,听着听着,你咧起嘴傻笑着,就睡着了。

2012年安徽中考语文试题及参考答案
父亲越来越老了,雪后的山路上,他再也不能健步如飞了。妻子说,年前我们干脆抽两天时间回去看看吧!回去那天,父亲正坐在火塘边,望着树上的橘子发呆,看到我们,父亲一愣,随即便孩子般叫着母亲的名字。

古诗词诵读《桂枝香?金陵怀古》说课稿(一) 2021-2022学年统编版高中语文必修下册
王安石,字介甫,号半山。北宋著名政治家、思想家、文学家、改革家,唐宋八大家之一。欧阳修称赞王安石:“翰林风月三千首,吏部文章二百年。老去自怜心尚在,后来谁与子争先。”传世文集有《王临川集》、《临川集拾遗》等。其诗文各体兼擅,词虽不多,但亦擅长,世人哄传之诗句莫过于《泊船瓜洲》中的“春风又绿江南岸,明月何时照我还。”且有名作《桂枝香》等。介绍之后设置这样的导入语:今天我们共同走进王安石,一起欣赏名作《桂枝香·金陵怀古》。(板书标题)(二)整体感知整体感知是赏析文章的前提,通过初读,可以使学生初步了解将要学到的基本内容,了解文章大意及思想意图,使学生对课文内容形成整体感知。首先,我会让学生根据课前预习,出声诵读课文,同时注意朗读的快慢、停顿、语调、轻重音等,然后再播放音频,纠正他们的读音与停顿。其次,我会引导学生谈谈他感受。学生通过朗读,能够说出本词雄壮、豪放、有气势,有对景物的赞美和对历史的感喟。

《一个消逝了的山村》说课稿 2021—2022学年统编版高中语文选择性必修下册
这几段内容传达出的是“要敬畏生命,尊重生命;更要敬畏大自然,尊重大自然,爱护大自然”的主旨内涵,因此让学生通过自由朗读的方式,再次体会冯至对这个消逝了的山村的细致的美好的描绘,感悟冯至传达出的对生命,对自然的理解和思考。5.最后一个自然段的解读依然是交给学生,先齐读课文,再让学生自主分享自己的体会或疑惑。但在这一环节我也设计了两个我认为必须解答的两个问题,一是怎么理解“在风雨如晦的时刻”;二是“意味不尽的关联”是指什么。我认为这两个问题一个涉及到写作背景,一个涉及到对全文主旨的一个整体把握,能够进一步帮助学生理解散文的深刻内涵和主旨,让学生有意识的在阅读散文过程中通过背景知识进行理解。既尊重学生的个性化解读,又能够让学生有意义学习,完成预设的教学目标。如果学生没有提到这两处,那我就需要做出补充。

古诗词诵读《拟行路难(其四)》说课稿 2021-2022学年统编版高中语文选择性必修下册
(一)导入新课“时势造英雄”,恶劣的环境造就名诗名篇。正因如此,怀才不遇于古人是恒久的情感素材。同学们,请大家回忆我们学过哪些抒发作者怀才不遇的诗词?(二)解释题意拟:仿照,模拟《行路难》,是乐府杂曲,本为汉代歌谣,晋人袁山松改变其音调,创制新词,流行一时。 鲍照《拟行路难》共十八首,歌咏人世的种种忧虑,寄寓悲愤,今天我们学习的是其中第四首。(三)作者简介、写作背景门阀制度之下,“上品无寒门,下品无世族”,出身寒微的文人往往空怀一腔热忱,却报国无门,不得不在壮志未酬的遗恨中坐视时光流逝。即使跻身仕途,也多是充当幕僚、府掾,备受压抑,在困顿坎坷中徒然挣扎,只落得身心交瘁。

古诗词诵读《桂枝香?金陵怀古》说课稿(二) 2021-2022学年统编版高中语文必修下册
一、教材解析《桂枝香·金陵怀古》选自统教版必修下册古诗词诵读单元,此词通过对金陵景物的赞美和历史兴亡的感喟,寄托了作者对当时朝政的担忧和对国家政治大事的关心。全词情景交融,境界雄浑阔大,风格沉郁悲壮,把壮丽的景色和历史内容和谐地融合在一起,自成一格,堪称名篇。二、学情分析高中一年级的学生已具有一定的诗歌阅读鉴赏能力,对学生来说,最重要的是积累诵读方法,提升鉴赏能力。在本文的教学过程中着重落实“读”,通过多样化的“读”,提升对诗歌“美”的感悟鉴赏能力。三、教学目标从课程标准中“全面提高学生语文素养”的基本理念出发,我设计了以下教学目标:1.语言建构与运用:疏通疑难字词,读懂诗句体会词的诵读要领。
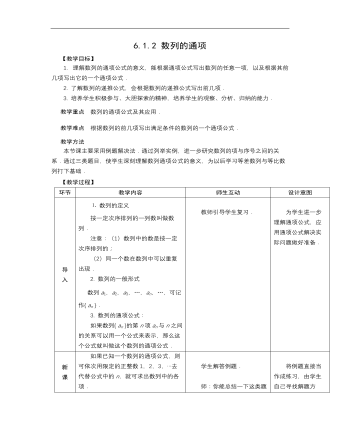
高教版中职数学基础模块下册:6.1《数列的概念》教案设计
【教学目标】1. 理解数列的通项公式的意义,能根据通项公式写出数列的任意一项,以及根据其前几项写出它的一个通项公式.2. 了解数列的递推公式,会根据数列的递推公式写出前几项.3.培养学生积极参与、大胆探索的精神,培养学生的观察、分析、归纳的能力.教学重点 数列的通项公式及其应用.教学难点 根据数列的前几项写出满足条件的数列的一个通项公式.教学方法 本节课主要采用例题解决法.通过列举实例,进一步研究数列的项与序号之间的关系.通过三类题目,使学生深刻理解数列通项公式的意义,为以后学习等差数列与等比数列打下基础.【教学过程】 环节教学内容师生互动设计意图导 入⒈数列的定义 按一定次序排列的一列数叫做数列. 注意:(1)数列中的数是按一定次序排列的; (2)同一个数在数列中可以重复出现. 2. 数列的一般形式 数列a1,a2,a3,…,an,…,可记作{ an }. 3. 数列的通项公式: 如果数列{ an }的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 教师引导学生复习. 为学生进一步理解通项公式,应用通项公式解决实际问题做好准备.

高教版中职数学基础模块下册:6.3《等比数列》优秀教案设计
授课 日期 班级16高造价 课题: §6.3等比数列 教学目的要求: 1.理解等比数列的概念,能根据定义判断或证明一个数列是等比数列;2.探索并掌握等比数列的通项公式; 3.掌握等比数列前 n 项和公式及推导过程,能用公式求相关参数; 教学重点、难点:运用等比数列的通项公式求相关参数 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》 授课执行情况及分析: 板书设计或授课提纲 §6.3等比数列 1.等比数列的概念 (学生板书区) 2. 等比数列的通项公式 3.等比数列的求和公式

