-

《乡间的小路》教案
教学过程:1、导入:(课前音乐:课堂里回荡着悠扬的歌声《小路》,学生在歌声中走进课堂。课前酝酿“乡间小路”的气氛。)(1)提问导入:同学们,你们了解校园民谣吗?你们听过的校园民谣有哪些呢?大家说了这么多,老师忍不住也想唱了,请同学们一起来和老师感受一下吧。师和音乐伴奏范唱《乡间的小路》。2、提问:你听到了什么,感受到了什么?能有感情的朗读出来吗?在萨克斯《归家》音乐声中有感情的朗诵《乡间的小路》,体会歌曲意境。歌词里所描写的景色多么迷人啊!你看“乡间的小路、暮归的老牛、蓝天、夕阳、云彩”,还有“牧童的歌声、笛声”,这一切都是那么的安详惬意,不管我们有多少的烦恼惆怅,只要走在乡间的小路上,它们都会随风飘散,消失得无影无踪。这么优美如诗、风光如画的歌曲,让我们再聆听一遍,请大家一边视听一边思考:歌曲可以分为几个部分?每个部分给你的情绪感受都是一样的吗?播放歌曲视频。3、新课:(1)欣赏歌曲《乡间的小路》,边听边用脚轻踩拍子,注意重拍。 a、歌曲所表现的内容是什么?情绪如何? b、歌曲的重拍在哪?是几拍子?(第二遍聆听)

中班音乐教案:大鼓与小鼓
2. 学会唱《大鼓与小鼓》这首歌。 重点: 辨别区分声音的强弱。 难点: 会正确表现声音的强弱。 活动准备: 大鼓、小鼓。 活动过程: 1. 用身体动作表现强与弱。如:拍手和点手心,拍手心和拍手背,拍腿和拍肩等。 2. 认识强弱记号。 教师准备两幅图片,上面画有f和p,告诉小朋友f表示强,p表示弱,并用动作表示出来。

《你是这样的人》教案
教学课题:1、欣赏并演唱《你是这样的人》。2、欣赏并朗诵表现总理的诗歌。3、跟老师唱《为了谁》,从中感受英雄人物的无私奉献精神。教学目标:1、能饱含深情地演唱《你是这样的人》,体验表现对周总理的怀念崇敬之情。2、感受诗歌如何塑造总理的光辉形象。3、通过演唱歌曲,感受英雄人物的无私奉献精神,从而感悟人生、树立正确的世界观和人生观。教学分析:这是大型电视艺术片《百年恩来》的主题歌。歌曲分为两个部分。第一部分:旋律委婉深情,节奏平稳规整,把一个伟人沉稳的形象表现得淋漓尽致。这一主题在第二部分中也多次出现,使两部分紧紧相扣。第二部分:表达了对伟人的无限怀念。这首歌在创作风格上一改过去歌颂伟人的模式,旋律以深沉、凝重见长,歌词也以抒情为主。以“人之情”替代了口号似的语言,仿佛周总理那微笑的神情又展现在我们面前,总理博爱的精神和博大的胸怀影响着一代又一代人。

《你是这样的人》教案
教学内容:1、欣赏并演唱歌曲《你是这样的人》。2、欣赏表现总理的诗、歌、画和摄影作品。教学目标:1、能饱含深情地演唱歌曲《你是这样的人》,尝试用自己设计的力度、速度和音色变化来表现歌曲的情感。2、感受诗、歌、画、摄影等艺术作品,是如何塑造总理的光辉形象、表现人们对总理的深厚情感。体会音乐及相关的诗歌、美术、摄影作品塑造任务形象的特点。3、能对表现革命领袖和英雄人物的音乐感兴趣,从中感受老一辈革命家的革命情怀和为革命无私奉献的精神,感受人民对总理的热爱、崇敬之情。教材分析:《你是这样的人》是为纪念周恩来诞辰100周年而作的大型电视艺术片《百年恩来》的主题歌。歌曲以深刻凝练的语言。表现了人们对周总理的敬仰之情,表达了人们对他的深切缅怀和无限爱戴。这首歌曲融合了西洋歌剧、音乐剧和流行歌曲的诸多元素、听来荡气回肠。

《你是这样的人》教案
简析歌曲 (6分钟)这首歌曲是大型电视艺术片《百年恩来》的主题歌,为纪念周总理诞辰100周年而创作的。这是一首抒情歌曲,(上册学过)全曲分两段,第一段音乐抒缓,颂扬了伟人的品格;第二段音乐激昂,与第一段形成对比。歌曲由著名的男高音歌唱家戴玉强演唱,他的演唱充满了激情,唤起了对伟人的无比怀念。周恩来(1898.3.5—1976.1.8)生于江苏淮安,新中国成立后一直担任政务院、国务院总理,他的一生可以说是鞠躬尽瘁、死而后已,为新中国的建设奋斗了一生。他少年时代就立下了“为中华之崛起而读书”的名言。周总理逝世后联合国为他降半旗。抒情歌曲:是声乐作品的一种体裁。其表现范围极为宽广,现实中的一切情感,如欢乐、怀念、期盼、痛苦、忧伤、激愤……都可以通过歌声得以抒发。

牛顿第一定律教案 3篇
①他的观点来源于伽利略的理想实验。 ②观点:物体不受力时,将保持自己的速度永远运动下去。 3.牛顿第一定律: ①来源于牛顿第一定律实验。 ②定律:一切物体总保持匀速直线运动状态或静止状态,直到有外力迫使它改变这种状态为止。

第四单元“神话故事”教案
(1)了解故事的起因、经过、结果,感受神话中的人物形象。这是本单元的语文要素,引导学生体会神话永久的魅力,人类神话时代飞腾的幻想。引导学生通过对课文的整体把握,和对重点词句的理解,感受到古代神话故事中人物形象,性格特点。能引导学生根据想象描写人物,感受神话故事中人物的神奇。盘古雄伟、高大的形象;精卫的坚强不屈、坚韧不拔的性格;普罗米修斯的勇敢与献身精神;女娲的勇敢、善良的品质,跃然在纸上,展现在我们面前。教学时注意引导学生发现神话故事的特点,感受神话的神奇。

必修一牛顿第一定律教案
(二)?过程与方法? 4.?观察生活中的惯性现象,了解力和运动的关系? 5.?通过实验加深对牛顿第一定律的理解? 6.?理解理想实验是科学研究的重要方法? (三)?情感态度与价值观? 7.?通过伽利略和亚里士多德对力和运动关系的不同认识,了解人类认识事物本质的曲折性? 8.?感悟科学是人类进步的不竭动力

《匈牙利狂想曲第二号》教案
教学过程:一、导入1、问题导入。师:猜猜这位大师是谁?【课件】生:回答。2、了解乐曲作曲家及相关知识。师:李斯特是著名的匈牙利作曲家。少年时期他随父母去了巴黎,成名以后回到祖国,广泛收集匈牙利民歌和吉普赛音乐,写下了19首在其创作中占有重要地位的匈牙利狂想曲。这些音乐具有匈牙利吉普赛人的热情,是匈牙利民族音乐的杰出作品,其中尤以第二号匈牙利狂想曲最为著名。二、学习歌曲师:这首狂想曲以匈牙利民间舞曲查尔达什体裁写成,分成庄重慢板和奔放急板两大部分。乐曲前半部分在滞缓的节奏衬托下,低沉压抑的旋律蕴含了巨大的悲愤,表现了匈牙利人不屈的性格。尤其是引子部分,在这一段中,右手是弹奏长音,左手是弹奏带装饰音的八分音符;大小和弦交替进行,声音不适宜太长,太长了显得松弛,要具有力度和爆发感。(接着乐曲在高音区反复并转入舞曲风格的轻快曲调,富有动力性。第二部分乐曲的速度加快,先奏出舞曲的主题,然后力度再逐渐增加,速度越来越快;接着涌现了一个个富有个性的主题,音乐的高潮此起彼伏,如旋风般旋转的舞曲在狂热的高潮中结束。)

北师大初中数学九年级上册用树状图或表格求概率1教案
由上表可知,共有6种结果,且每种结果是等可能的,其中两次摸出白球的结果有2种,所以P(两次摸出的球都是白球)=26=13;(2)列表如下:第一次第二次 白1 白2 红白1 (白1,白1) (白2,白1) (红,白1)白2 (白1,白2) (白2,白2) (红,白2)红 (白1,红) (白2,红) (红,红)由上表可知,共有9种结果,且每种结果是等可能的,其中两次摸出白球的结果有4种,所以P(两次摸出的球都是白球)=49.方法总结:在试验中,常出现“放回”和“不放回”两种情况,即是否重复进行的事件,在求概率时要正确区分,如利用列表法求概率时,不重复在列表中有空格,重复在列表中则不会出现空格.三、板书设计用树状图或表格求概率画树状图法列表法通过与学生现实生活相联系的游戏为载体,培养学生建立概率模型的思想意识.在活动中进一步发展学生的合作交流意识,提高学生对所研究问题的反思和拓展的能力,逐步形成良好的反思意识.鼓励学生思维的多样性,发展学生的创新意识.

北师大初中数学九年级上册用树状图或表格求概率1教案
由上表可知,共有6种结果,且每种结果是等可能的,其中两次摸出白球的结果有2种,所以P(两次摸出的球都是白球)=26=13;(2)列表如下:由上表可知,共有9种结果,且每种结果是等可能的,其中两次摸出白球的结果有4种,所以P(两次摸出的球都是白球)=49.方法总结:在试验中,常出现“放回”和“不放回”两种情况,即是否重复进行的事件,在求概率时要正确区分,如利用列表法求概率时,不重复在列表中有空格,重复在列表中则不会出现空格.三、板书设计用树状图或表格求概率画树状图法列表法通过与学生现实生活相联系的游戏为载体,培养学生建立概率模型的思想意识.在活动中进一步发展学生的合作交流意识,提高学生对所研究问题的反思和拓展的能力,逐步形成良好的反思意识.鼓励学生思维的多样性,发展学生的创新意识.

北师大初中数学八年级上册一定是直角三角形吗1教案
方法总结:利用三角形三边的数量关系来判定直角三角形,从而推出两线的垂直关系.探究点二:勾股数下列几组数中是勾股数的是________(填序号).①32,42,52;②9,40,41;③13,14,15;④0.9,1.2,1.5.解析:第①组不符合勾股数的定义,不是勾股数;第③④组不是正整数,不是勾股数;只有第②组的9,40,41是勾股数.故填②.方法总结:判断勾股数的方法:必须满足两个条件:一要符合等式a2+b2=c2;二要都是正整数.三、板书设计勾股定理的逆定理: 如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.勾股数:满足a2+b2=c2的三个正整数,称为勾股数.经历一般规律的探索过程,发展学生的抽象思维能力、归纳能力.体验生活中数学的应用价值,感受数学与人类生活的密切联系,激发学生学数学、用数学的兴趣.

北师大初中数学九年级上册利用两角判定三角形相似1教案
解:方法一:因为DE∥BC,所以∠ADE=∠B,∠AED=∠C,所以△ADE∽△ABC,所以ADAB=DEBC,即44+8=5BC,所以BC=15cm.又因为DF∥AC,所以四边形DFCE是平行四边形,所以FC=DE=5cm,所以BF=BC-FC=15-5=10(cm).方法二:因为DE∥BC,所以∠ADE=∠B.又因为DF∥AC,所以∠A=∠BDF,所以△ADE∽△DBF,所以ADDB=DEBF,即48=5BF,所以BF=10cm.方法总结:求线段的长,常通过找三角形相似得到成比例线段而求得,因此选择哪两个三角形就成了解题的关键,这就需要通过已知的线段和所求的线段分析得到.三、板书设计(1)相似三角形的定义:三角分别相等、三边成比例的两个三角形叫做相似三角形;(2)相似三角形的判定定理1:两角分别相等的两个三角形相似.感受相似三角形与相似多边形、相似三角形与全等三角形的区别与联系,体验事物间特殊与一般的关系.让学生经历从实验探究到归纳证明的过程,发展学生的合情推理能力,培养学生的观察、动手探究、归纳总结的能力.

北师大初中数学九年级上册利用三边判定三角形相似1教案
同理,图③中,三角形的三边长分别为2,5,3;同理,图④中,三角形的三边长分别为2,5,13.∵21=22=105=2,∴图②中的三角形与△ABC相似.方法总结:(1)各个图形中的三角形均为格点三角形,可以根据勾股定理求出各边的长,然后根据三角形三边的长度是否成比例来判断两个三角形是否相似;(2)判断三边是否成比例,可以将三角形的三边长按大小顺序排列,然后分别计算他们对应边的比,最后由比值是否相等来确定两个三角形是否相似.三、板书设计相似三角形的判定定理3:三边成比例的两个三角形相似.从学生已学的知识入手,通过设置问题,引导学生进行计算、推理和归纳,提高分析问题和解决问题的能力.感受两个三角形相似的判定定理3与全等三角形判定定理(SSS)的区别与联系,体会事物间一般到特殊、特殊到一般的关系.让学生经历从实验探究到归纳证明的过程,发展学生的合情推理能力,培养学生与他人交流、合作的意识和品质.

北师大初中数学九年级上册位似多边形及其性质1教案
①分别连接OA,OB,OC,OD,OE;②分别在AO,BO,CO,DO,OE上截取OA′,OB′,OC′,OD′,OE′,使OA′OA=OB′OB=OC′OC=OD′OD=OE′OE=13;③顺次连接A′B′,B′C′,C′D′,D′E′,E′A′.五边形A′B′C′D′E′就是所求作的五边形;(3)画法如下:①分别连接AO,BO,CO,DO,EO,FO并延长;②分别在AO,BO,CO,DO,EO,FO的延长线上截取OA′,OB′,OC′,OD′,OE′,OF′,使OA′OA=OB′OB=OC′OC=OD′OD=OE′OE=OF′OF=12;③顺次连接A′B′,B′C′,C′D′,D′E′,E′F′,F′A′.六边形A′B′C′D′E′F′就是所求作的六边形.方法总结:(1)画位似图形时,要注意相似比,即分清楚是已知原图与新图的相似比,还是新图与原图的相似比.(2)画位似图形的关键是画出图形中顶点的对应点.画图的方法大致有两种:一是每对对应点都在位似中心的同侧;二是每对对应点都在位似中心的两侧.(3)若没有指定位似中心的位置,则画图时位似中心的取法有多种,对画图而言,以多边形的一个顶点为位似中心时,画图最简便.三、板书设计
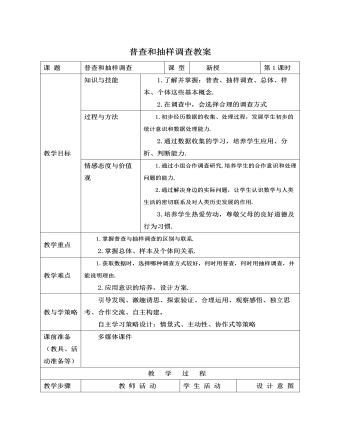
北师大初中七年级数学上册普查和抽样调查教案2
1.举例说明什么时候用普查的方式获得数据较好,什么时候用抽样调查的方式获得数据较好?2、下列调查中分别采用了那些调查方式?⑴为了了解你们班同学的身高,对全班同学进行调查.⑵为了了解你们学校学生对新教材的喜好情况,对所有学号是5的倍数的同学进行调查。3、说明在以下问题中,总体、个体、样本各指什么?⑴为了考察一个学校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.⑵为了了解一批电池的寿命,从中抽取10只进行实验。⑶为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计。通过本节课的学习,同学们有什么收获和疑问?1、基本概念:⑴.调查、普查、抽样调查.⑵.总体、个体、样本.2、何时采用普查、何时采用抽样调查,各有什么优缺点?

北师大初中数学九年级上册一元二次方程2教案
三、课堂检测:(一)、判断题(是一无二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1. 5x2+1=0 ( ) 2. 3x2+ +1=0 ( )3. 4x2=ax(其中a为常数) ( ) 4.2x2+3x=0 ( )5. =2x ( ) 6. =2x ( ) (二)、填空题.1.方程5(x2- x+1)=-3 x+2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.2.如果方程ax2+5=(x+2)(x-1)是关于x的一元二次方程,则a__________.3.关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程。四、学习体会:五、课后作业
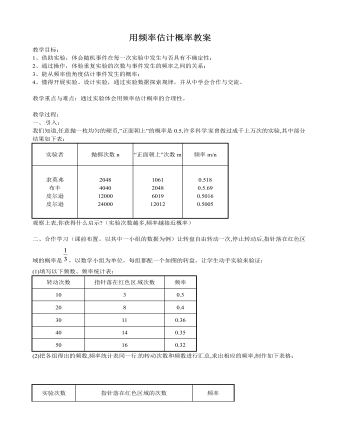
北师大初中数学九年级上册用频率估计概率2教案
(4)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发 生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率。三、做一做:1.某运动员投篮5次, 投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2.回答下列问题:(1)抽检1000件衬衣,其中不合格的衬衣有2件,由 此估计抽1件衬衣合格的概率是多少?(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?

北师大初中七年级数学上册利用去分母解一元一次方程教案2
先让学生自己总结,然后互相交流,得出结论。解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式。解题时,要灵活运用这些步骤。板书:解一元一次方程一般步骤:1、 去分母-----等式性质22、 去括号----去括号法则3、 移项----等式性质14、 合并同类项----合并同类项法则5、 系数化为1.----等式性质2【课堂练习】练习:解下列一元一次方程解方程: (2) ;思路点拔:(1)去分母所选的乘数应是所有分母的最小公倍数,不应遗漏。(2)用分母的最小公倍数去乘方程的两边时,不要漏掉等号两边不含分母的项。(3)去掉分母后,分数线也同时去掉,分子上的多项式用括号括起来。回顾解以上方程的全过程,表示了一元一次方程解法的一般步骤,通过去分母—去括号—移项—合并同类项—系数化为1等步骤,就可以使一元一次方程逐步向着 =a的形式转化。
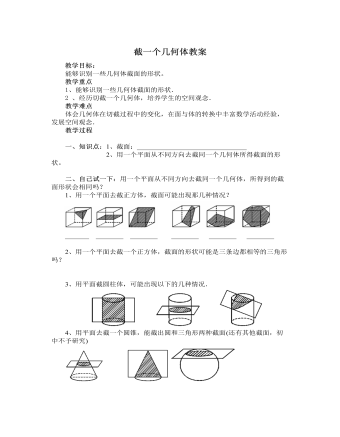
北师大初中七年级数学上册截一个几何体教案2
[例3]、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是_________。四、巩固强化:1、一个正方体的截面不可能是( )A、三角形 B、梯形 C、五边形 D、七边形2、用一个平面去截五棱柱,边数最多的截面是_______形.3*、用一个平面去截几何体,若截面是三角形,这个几何体可能是__________________________________________________.4*、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如虹截面是三角形呢?5*、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?6*、几何体中的圆台、棱锥都是课外介绍的,所以我们就在这个栏目里继续为大家介绍这两种几何体的截面.(1)圆台用平面截圆台,截面形状会有_____和_______这两种较特殊图形,截法如下:

