-
人教版新课标高中物理必修1匀变速直线运动的速度与时间的关系教案2篇
一、设计思想通过本节教学,不但要使学生认识掌握匀变速直线运动的规律,而且要通过对这问题的研究,使学生了解和体会物理学研究问题的一个方法,图象、公式、以及处理实验数据的方法等。这一点可能对学生更为重要,要通过学习过程使学生有所体会。本节在内容的安排顺序上,既注意了科学系统,又注意学生的认识规律。讲解问题从实际出发,尽量用上一节的实验测量数据。运用图象这种数学工具,相对强调了图象的作用和要求。这是与以前教材不同的。在现代生产、生活中,图象的运用随处可见,无论学生将来从事何种工作,掌握最基本的应用图象的知识,都是必须的。学生在初学时往往将数学和物理分割开来,不习惯或不会将已学过的数学工具用于物理当中。在教学中应多在这方面引导学生。本节就是一个较好的机会,将图象及其物理意义联系起来。

人教版新课标高中物理必修1匀变速直线运动的位移与时间的关系教案2篇
一、教学目标1.知识与技能:(1)知道匀速直线运动的位移x=υt对应着 图象中的矩形面积.(2)掌握匀变速直线运动的位移与时间关系的公式 ,及其简单应用.(3)掌握匀变速直线运动的位移与速度关系的公式 ,及其简单应用.2.过程与方法:(1)让学生初步了解探究学习的方法.(2)培养学生运用数学知识-----函数图象的能力.(3)培养学生运用已知结论正确类比推理的能力.3.情感态度与价值观:(1)培养学生认真严谨的科学分析问题的品质.(2)从知识是相互关联、相互补充的思想中,培养学生建立事物是相互联系的唯物主义观点.(3)培养学生应用物理知识解决实际问题的能力.二、教学重点、难点1.教学重点及其教学策略:重点:(1)匀变速直线运动的位移与时间关系的公式 及其应用.(2)匀变速直线运动的位移与速度关系的公式 及其应用.教学策略:通过思考讨论和实例分析来加深理解.

人教版新课标高中物理必修1匀变速直线运动的位移与时间的关系教案2篇
一、教学目标1.知识与技能:(1)知道匀速直线运动的位移x=υt对应着 图象中的矩形面积.(2)掌握匀变速直线运动的位移与时间关系的公式 ,及其简单应用.(3)掌握匀变速直线运动的位移与速度关系的公式 ,及其简单应用.2.过程与方法:(1)让学生初步了解探究学习的方法.(2)培养学生运用数学知识-----函数图象的能力.(3)培养学生运用已知结论正确类比推理的能力.3.情感态度与价值观:(1)培养学生认真严谨的科学分析问题的品质.(2)从知识是相互关联、相互补充的思想中,培养学生建立事物是相互联系的唯物主义观点.(3)培养学生应用物理知识解决实际问题的能力.二、教学重点、难点1.教学重点及其教学策略:重点:(1)匀变速直线运动的位移与时间关系的公式 及其应用.(2)匀变速直线运动的位移与速度关系的公式 及其应用.教学策略:通过思考讨论和实例分析来加深理解.

用空间向量研究直线、平面的位置关系(2)教学设计人教A版高中数学选择性必修第一册
跟踪训练1在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC;(2)BD1⊥EB1.(2)∵(BD_1 ) ?=(-1,-1,1),(EB_1 ) ?=(1/2 "," 1/2 "," 1),∴(BD_1 ) ?·(EB_1 ) ?=(-1)×1/2+(-1)×1/2+1×1=0,∴(BD_1 ) ?⊥(EB_1 ) ?,∴BD1⊥EB1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E(1/2 "," 1/2 "," 0),B1(1,1,1).(1)∵(BD_1 ) ?=(-1,-1,1),(AC) ?=(-1,1,0),∴(BD_1 ) ?·(AC) ?=(-1)×(-1)+(-1)×1+1×0=0.∴(BD_1 ) ?⊥(AC) ?,∴BD1⊥AC.例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.思路分析一种思路是不建系,利用基向量法证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直,从而根据线面垂直的判定定理证得结论;另一种思路是建立空间直角坐标系,通过坐标运算证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直;还可以在建系的前提下,求得平面EFB1的法向量,然后说明(D_1 M) ?与法向量共线,从而证得结论.证明:(方法1)因为E,F,M分别为棱AB,BC,B1B的中点,所以(D_1 M) ?=(D_1 B_1 ) ?+(B_1 M) ?=(DA) ?+(DC) ?+1/2 (B_1 B) ?,而(B_1 E) ?=(B_1 B) ?+(BE) ?=(B_1 B) ?-1/2 (DC) ?,于是(D_1 M) ?·(B_1 E) ?=((DA) ?+(DC) ?+1/2 (B_1 B) ?)·((B_1 B) ?-1/2 (DC) ?)=0-0+0-1/2+1/2-1/4×0=0,因此(D_1 M) ?⊥(B_1 E) ?.同理(D_1 M) ?⊥(B_1 F) ?,又因为(B_1 E) ?,(B_1 F) ?不共线,因此D1M⊥平面EFB1.
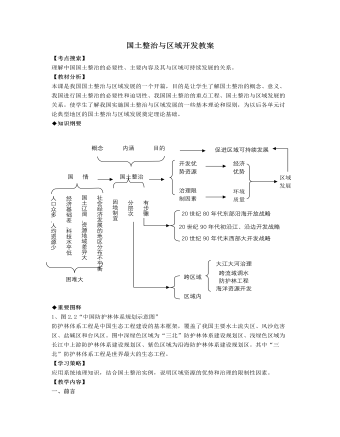
人教版高中地理选修2国土整治与区域开发教案
【考点搜索】理解中国国土整治的必要性、主要内容及其与区域可持续发展的关系。【教材分析】本课是我国国土整治与区域发展的一个开篇,目的是让学生了解国土整治的概念、意义、我国进行国土整治的必要性和迫切性、我国国土整治的重点工程、国土整治与区域发展的关系。使学生了解我国实施国土整治与区域发展的一些基本理论和原则,为以后各单元讨论典型地区的国土整治与区域发展奠定理论基础。◆重要图释1、图2.2“中国防护林体系规划示意图”防护林体系工程是中国生态工程建设的基本框架,覆盖了我国主要水土流失区、风沙危害区、盐碱区和台风区。图中深绿色区域为“三北”防护林体系建设规划区、浅绿色区域为长江中上游防护林体系建设规划区、紫色区域为沿海防护林体系建设规划区。其中“三北”防护林体系工程是世界最大的生态工程。

人教版高中地理选修2西南区交通运输建设与区域经济发展教案
1、图9.6“南昆铁路示意图”掌握南昆铁路起止点、支线、途经地区、铁路线附近的矿产资源(云南的磷矿、贵州的煤矿、广西的铝矿等);南昆铁路使西南区南连北海、防城港、湛江、钦州等港,成为西南区通往沿海地区最便捷的出海通道,使西南地区物资出海路程缩短了600千米,对西南区的发展具有十分重要的经济、政治、战略意义。2、图9.10“西南三省一市和广西主要铁路分布图”本图展现了西南三省一市和广西的主要铁路分布,要求重点掌握本区内的环状铁路——成渝-川黔-贵昆-成昆线,新建的南昆线、内昆线,以及宝成线(联系西北区),襄渝线、湘黔线和湘桂-黔桂线(联系中南区),枝柳线(联系中南区和华北区)等区际铁路,昆河线等国际铁路及重要铁路枢纽。3、图9.11“西藏自治区交通图”西藏自治区是我国目前唯一没有正式通铁路的省级行政区,读图后要能掌握联系拉萨的四大入藏(川藏、青藏、新藏、滇藏)公路及正在建设的青藏铁路。
小学数学苏教版六年级下册《第六单元第三课反比例关系、反比例量》教学设计说课稿
提问:1.怎样判断两种相关联的量是否成正比例?用字母怎样表示正比例关系? 2.判断下面两种量是否成正比例?为什么? (1)时间一定,行驶的路程和速度 (2)除数一定,被除数和商 3.单价、数量和总价之间有怎样的关系?在什么条件下,两种量成正比例? 4.导入新课: 如果总价一定,单价和数量的变化有什么规律?这两种量存在什么关系?今天,我们就来研究这种变化规律。

人教A版高中数学必修一集合间的基本关系教学设计(2)
第一节通过研究集合中元素的特点研究了元素与集合之间的关系及集合的表示方法,而本节重点通过研究元素得到两个集合之间的关系,尤其学生学完两个集合之间的关系后,一定让学生明确元素与集合、集合与集合之间的区别。课程目标1. 了解集合之间包含与相等的含义,能识别给定集合的子集.2. 理解子集.真子集的概念. 3. 能使用 图表达集合间的关系,体会直观图示对理解抽象概念的作用。数学学科素养1.数学抽象:子集和空集含义的理解;2.逻辑推理:子集、真子集、空集之间的联系与区别;3.数学运算:由集合间的关系求参数的范围,常见包含一元二次方程及其不等式和不等式组;4.数据分析:通过集合关系列不等式组, 此过程中重点关注端点是否含“=”及 问题;5.数学建模:用集合思想对实际生活中的对象进行判断与归类。

人教A版高中数学必修一同角三角函数的基本关系教学设计(2)
本节内容是学生学习了任意角和弧度制,任意角的三角函数后,安排的一节继续深入学习内容,是求三角函数值、化简三角函数式、证明三角恒等式的基本工具,是整个三角函数知识的基础,在教材中起承上启下的作用。同时,它体现的数学思想与方法在整个中学数学学习中起重要作用。课程目标1.理解并掌握同角三角函数基本关系式的推导及应用.2.会利用同角三角函数的基本关系式进行化简、求值与恒等式证明.数学学科素养1.数学抽象:理解同角三角函数基本关系式;2.逻辑推理: “sin α±cos α”同“sin αcos α”间的关系;3.数学运算:利用同角三角函数的基本关系式进行化简、求值与恒等式证明重点:理解并掌握同角三角函数基本关系式的推导及应用; 难点:会利用同角三角函数的基本关系式进行化简、求值与恒等式证明.

用空间向量研究直线、平面的位置关系(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、空间中点、直线和平面的向量表示1.点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量(OP) ?来表示.我们把向量(OP) ?称为点P的位置向量.如图.2.空间直线的向量表示式如图①,a是直线l的方向向量,在直线l上取(AB) ?=a,设P是直线l上的任意一点,则点P在直线l上的充要条件是存在实数t,使得(AP) ?=ta,即(AP) ?=t(AB) ?.如图②,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使(OP) ?=(OA) ?+ta, ①或(OP) ?=(OA) ?+t(AB) ?. ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.1.下列说法中正确的是( )A.直线的方向向量是唯一的B.与一个平面的法向量共线的非零向量都是该平面的法向量C.直线的方向向量有两个D.平面的法向量是唯一的答案:B 解析:由平面法向量的定义可知,B项正确.

人教版高中政治必修2处理民族关系的原则:平等、团结、共同繁荣教案
一、教材分析普通高中思想政治课程标准及浙江省普通高中新课程实验学科教学指导意见对本课时内容做了如下规定:基本要求:知道我国是统一的多民族国家;理解我国处理民族关系的三项基本原则及其相互关系;懂得处理民族关系的重要性,自觉履行维护国家统一和民族团结的义务。发展要求:联系国内外的具体事例,加深理解我国处理民族关系的基本原则的重要性。本框题有如下内容不作拓展:我们伟大的祖国是各族人民共同缔造的;我国新型民族关系的形成;实施西部大开发战略对加快民族自治地方的经济和社会发展的意义;我国能够真正建立新型民族的原因。《处理民族关系的原则:平等、团结、共同繁荣》是高一《政治生活》第三单元第七课内容,本课内容由三目构成,第一目:雪域高原的历史性跨越,第二目:我国处理民族关系的基本原则,第三目:巩固社会主义民族关系,我们该做什么,能做什么。

人教版高中地理选修5自然灾害与人类活动教案
(1)类型:常见的农作物病害有:稻瘟病、小麦锈病、棉花枯萎病、烟草炭疽病等。常见的森林病害有:杨树烂皮病、松疱锈病、溶叶病、泡桐丛枝病等。(2)病害发生的原因:A.气候变异等造成的不良环境使得作物对病害抗性降低。B.外来病原体入侵也是病害流行的主要原因。(3)危害:病害使农作物、树木染病从而枯萎甚至死株,导致大面积农田、森林被毁坏。2.虫害和鼠害(1)虫害的常见类型①常见的农作物虫害有:蝗虫、黏虫、水稻螟、棉铃虫等。其中危害最大的是蝗虫。②常见的森林虫害有松材线虫、松毛虫、杨树蛀干害虫、泡桐大袋蛾等。其中松材线虫是世界上最具危险性的森林虫害,被列为国际、国内重大检疫对象。(2)鼠害及危害①重灾区:农田、牧场及森林。②危害:害鼠啃食植株,在地下打洞,危害植物根系,使农业减产,森林草地遭到破坏。(3)虫、鼠害的特点:繁殖快、适应能力强(4)造成虫害和鼠害流行的因素:①适宜繁殖的气候条件、②自然或人为因素造成的天敌减少等,

人教A版高中数学必修一集合间的基本关系教学设计(1)
本节内容来自人教版高中数学必修一第一章第一节集合第二课时的内容。集合论是现代数学的一个重要基础,是一个具有独特地位的数学分支。高中数学课程是将集合作为一种语言来学习,在这里它是作为刻画函数概念的基础知识和必备工具。本小节内容是在学习了集合的含义、集合的表示方法以及元素与集合的属于关系的基础上,进一步学习集合与集合之间的关系,同时也是下一节学习集合间的基本运算的基础,因此本小节起着承上启下的关键作用.通过本节内容的学习,可以进一步帮助学生利用集合语言进行交流的能力,帮助学生养成自主学习、合作交流、归纳总结的学习习惯,培养学生从具体到抽象、从一般到特殊的数学思维能力,通过Venn图理解抽象概念,培养学生数形结合思想。

人教版高中地理选修2三峡工程对生态环境和名胜古迹的影响及对策教案
一、三峡工程的生态环境效应三峡工程的生态环境效应是指建设三峡工程对生态与环境的有利和不利影响。1、有利影响(1)防洪:(2)防治血吸虫病:(3)减轻洞庭湖淤积(4)增加枯水期流量,改善水(5)调节局部气候:(6)减轻环境污染:综上所述,三峡工程对生态环境的有利影响主要在中下游。2、不利影响及措施(1)淹没土地、耕地:水库蓄水将淹没土地、耕地。(2)加剧水土流失和环境污染:在移民开发和城市迁建过程中,处理不当可能产生新的水土流失和环境污染等问题。(3)诱发地质灾害(地震、滑坡):水库蓄水改变了原有地应力的平衡,可能诱发地震,并使库岸发生滑坡等地质灾害的可能性增大。(4)加重泥沙淤积:水库蓄水,使库区水流速度变慢,库区和库尾的泥沙淤积加重。
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
人教A版高中数学必修二有限样本空间与随机事件事件的关系和运算教学设计
新知讲授(一)——随机试验 我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示。我们通常研究以下特点的随机试验:(1)试验可以在相同条件下重复进行;(2)试验的所有可能结果是明确可知的,并且不止一个;(3)每次试验总是恰好出现这些可能结果中的一个,但事先不确定出现哪个结果。新知讲授(二)——样本空间思考一:体育彩票摇奖时,将10个质地和大小完全相同、分别标号0,1,2,...,9的球放入摇奖器中,经过充分搅拌后摇出一个球,观察这个球的号码。这个随机试验共有多少个可能结果?如何表示这些结果?根据球的号码,共有10种可能结果。如果用m表示“摇出的球的号码为m”这一结果,那么所有可能结果可用集合表示{0,1,2,3,4,5,6,7,8,9}.我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间。

小学数学人教版四年级下册《乘、除法的意义和各部分间的关系》说课稿
尊敬的各位评委老师: 你们好!我说课的内容是义务教育教科书人教版小学数学四年级下册第一单元第5-6页的内容《乘除法的意义和各部分间的关系》。下面我谈谈本节课的教学设想,不妥之处,恳请各位教师指正。一.我对教材的理解(教材分析)——参考教学参考书《乘除法的意义和各部分间的关系》是人教版小学四年级下册第一单元四则运算中第2课时的教学内容。本课是在学生对整数乘除法有了较多的接触,积累了丰富的感性认识并掌握了相应的基础知识和技能的基础上进行抽象、概括,上升到理性的认识。为后面学习的四则运算打基础,也为以后学习小数、分数的意义和关系做铺垫。二.学情分析(根据考评要求,可不说)因为年龄特征决定了四年级学生活泼好奇好动,虽具一定的抽象思维能力,但仍然以形象思维为主;就知识层面上,已经学习了简单整数乘除法,对整数乘除法及各部分名称有初步的感性认知,初步具备了理性认知学习的基础;同时又存在个体差异,多数学生思维活跃,数学兴趣浓厚,表现欲望强烈,少数学生缺乏积极性,学习被动。

人教版高中数学选修3成对数据的相关关系教学设计
由样本相关系数??≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同.归纳总结1.线性相关系数是从数值上来判断变量间的线性相关程度,是定量的方法.与散点图相比较,线性相关系数要精细得多,需要注意的是线性相关系数r的绝对值小,只是说明线性相关程度低,但不一定不相关,可能是非线性相关.2.利用相关系数r来检验线性相关显著性水平时,通常与0.75作比较,若|r|>0.75,则线性相关较为显著,否则不显著.例2. 有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如表所示.画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.

小学数学人教版五年级下册《第六课体积单位间的进率》教案说课稿
(一)复习旧知,导入新课。师:同学们,上节课我们认识了体积和体积单位,请你填一填这两道题,看看你学得怎么样。(课件第2张)1.常用的体积单位有(立方厘米)、(立方分米)、(立方米),可以分别写成(cm³) 、(dm³)、 (m³)。2.棱长是1cm的正方体,体积是(1cm³)。3.棱长是1dm的正方体,体积是(1dm³)。4.棱长是1m的正方体,体积是(1m³)。【设计意图】1dm³是多少cm³呢?这节课我们就来研究一下体积单位间的进率。(板书课题)(二)探究新知1.探究立方分米和立方厘米间的进率:(课件第3张)(1)下图是一个棱长为1dm的正方体,体积是1dm³。想一想,它的体积是多少立方厘米呢?(2)小组讨论,你是怎样想的?(3)汇报交流:(课件第4张)生1:如果把它的棱长看作是10cm,可以把它切成1000块1cm³的小正方体。10×10×10=1000.生2:它的底面积是1dm²,就是100cm²,100×10=1000,一共是1000cm³。1dm³=1000cm³【设计意图】用小组讨论的方式,让学生从讨论的过程中找到解决问题的方法,培养学生的语言表达能力、思维能力。2.你知道1m³等于多少立方分米吗?(课件第5张)生1:把棱长是1m的正方体,看作棱长是10dm的正方体,10×10×10=1000dm³。1m³=1000dm³。 生2:棱长是1m的正方体,底面积是1m²,就是100dm²,100×10=1000dm³,一共是1000dm³。生3:1m³=1000dm³ 3.整理计量单位之间的进率。(1)小组讨论:到现在为止,我们已经学习了哪些计量单位?请整理在表中。

人教版新课标高中地理必修2第一章第二节人口的空间变化教案
1.促使美国成为一个移民国家的因素是:①美洲属于未开发的新大陆,需要大量的劳动力;②欧洲失业工人和破产农民增加,人们为了追求更好的经济待遇迁往美洲;③新航线的开辟为人们顺利迁移扫除了障碍;④殖民扩张是人口迁移的促进因素,加快了人口迁移的过程。导致美国人口在本土范围内频繁迁移的原因,归纳起来有:第一次人口迁移是战争因素,第二次是城市化;第三次是自然环境、经济环境的变化;第四次是经济格局的变化,即西部和南部新资源的发现和新兴工业的发展。2.我国古代的人口迁移,深受统治者及其行政力量的束缚。封建帝王为了加强本国的经济和军事实力,对人口迁移严加控制。只有当战乱发生的时候,这种控制才得到削弱,人们为了躲避战乱,寻找安定的生活环境,不得不进行大规模的迁移。我国近几十年的人口迁移主要是由生产资料和劳动力数量上的地区分布不平衡造成的,是经济因素在起主导作用,与古代的人口迁移截然不同。





















