-
2024年人大代表建议和政协提案办理工作总结的报告汇编（11篇）
一、基本情况本届两会，我委共收到区人大代表建议x件,其中主办x件，会办x件;区政协提案xx件，其中主办xx件（含组织提案x件），协办xx件。主要涉及数字经济、城市数字化转型、国际消费中心城市建设、中小企业发展、跨境电商产业发展、文化创意产业发展、菜市场业态改造等方面，其中，产业经济发展类的xx件，占总数的xx.x%；民生项目类的共x件，占总数的xx.x%。从总体情况看，今年我委承办的代表建议、政协提案具有以下三个特点：一是数量有所下降，人大建议数量与去年持平，政协提案较去年减少了xx件。二是关注经济发展新热点，建议和提案围绕后疫情时代大背景下，xxxx年我区经济新热点，如数字经济、城市数字化转型、中小企业发展等方面建言献策。三是紧扣民生问题，对社区就医、买菜难、菜市场业态改造等ZT，客观反映问题，提出相应的对策。
市水利局2023年度人大代表建议和政协提案办理工作总结
对市政协委员关于中小河流治理、农村供水改造提升的提案，我局以办理工作为契机，瞄准问题，精准发力，扎实推进中小河流治理、农村供水改造提升工作再上新台阶。今年以来，以实施淡水河、公庄河、永汉河等河流综合治理为抓手，预计全年新增治理中小河流28公里。今年实施的127宗农村小型供水工程消毒设施安装项目已全部完成，受益群众XX万人；5宗示范供水改造提升工程有1宗已完成，另外4宗正有条不紊推进，预计今年年底前全部完成，为我市下来推进农村供水“三同五化”提供可借鉴、可推广的好经验、好做法。2023年，在市政府正确领导以及市人大、市政协监督和支持下，我局顺利完成了人大代表建议和政协提案办理工作，取得较好成效。但个别建议提案的办理工作还不能完全达到上级要求，与人大代表、政协委员和人民群众的期盼仍有一定差距。下来，我局将进一步增强做好建议提案办理工作的责任感和使命感，坚持新发展理念，坚持高质量办理，推动人大建议和政协提案办理工作再上新台阶，更好地助力水利高质量发展。
婚礼策划婚庆策划方案
1 送亲人数： 位2 女方家中放炮与撒花人员：男方派人派车过去；3在家中女婿给岳父岳母改口、敬茶、老人给红包，并认亲；4新娘父母及亲属到酒店的车辆安排
【高教版】中职数学拓展模块：3.3《离散型随机变量及其分布》教学设计
重点分析：本节课的重点是离散型随机变量的概率分布，难点是理解离散型随机变量的概念． 离散型随机变量 突破难点的方法： 函数的自变量 随机变量 连续型随机变量 函数可以列表 X123456p 2 4 6 8 10 12
人教A版高中数学必修二总体离散程度的估计教学设计
问题二：上述问题中，甲、乙的平均数、中位数、众数相同，但二者的射击成绩存在差异，那么，如何度量这种差异呢？我们可以利用极差进行度量。根据上述数据计算得：甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息，所含的信息量很少。也就是说，极差度量出的差异误差较大。问题三：你还能想出其他刻画数据离散程度的办法吗？我们知道，如果射击的成绩很稳定，那么大多数的射击成绩离平均成绩不会太远；相反，如果射击的成绩波动幅度很大，那么大多数的射击成绩离平均成绩会比较远。因此，我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
点到直线的距离公式教学设计人教A版高中数学选择性必修第一册
4.已知△ABC三个顶点坐标A(－1,3)，B(－3,0)，C(1,2)，求△ABC的面积S.【解析】由直线方程的两点式得直线BC的方程为 ＝ ，即x－2y＋3＝0，由两点间距离公式得|BC|＝ ，点A到BC的距离为d，即为BC边上的高，d＝ ，所以S＝ |BC|·d＝ ×2 × ＝4，即△ABC的面积为4.5.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.解:(方法一)∵点A(1,1)与B(-3,1)到y轴的距离不相等,∴直线l的斜率存在,设为k.又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.由点A(1,1)与B(-3,1)到直线l的距离相等,∴直线l的方程是y=2或x-y+2=0.得("|" k"-" 1+2"|" )/√(k^2+1)=("|-" 3k"-" 1+2"|" )/√(k^2+1),解得k=0或k=1.(方法二)当直线l过线段AB的中点时,A,B两点到直线l的距离相等.∵AB的中点是(-1,1),又直线l过点P(0,2),∴直线l的方程是x-y+2=0.当直线l∥AB时,A,B两点到直线l的距离相等.∵直线AB的斜率为0,∴直线l的斜率为0,∴直线l的方程为y=2.综上所述,满足条件的直线l的方程是x-y+2=0或y=2.
两点间的距离公式教学设计人教A版高中数学选择性必修第一册
一、情境导学在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小?二、探究新知问题1.在数轴上已知两点A、B，如何求A、B两点间的距离？提示：|AB|＝|xA－xB|.问题2：在平面直角坐标系中能否利用数轴上两点间的距离求出任意两点间距离？探究.当x1≠x2，y1≠y2时，|P1P2|＝？请简单说明理由．提示：可以，构造直角三角形利用勾股定理求解．答案：如图，在Rt △P1QP2中，|P1P2|2＝|P1Q|2＋|QP2|2，所以|P1P2|＝?x2－x1?2＋?y2－y1?2.即两点P1(x1，y1)，P2(x2，y2)间的距离|P1P2|＝?x2－x1?2＋?y2－y1?2.你还能用其它方法证明这个公式吗？2．两点间距离公式的理解(1)此公式与两点的先后顺序无关，也就是说公式也可写成|P1P2|＝?x2－x1?2＋?y2－y1?2.(2)当直线P1P2平行于x轴时，|P1P2|＝|x2－x1|.当直线P1P2平行于y轴时，|P1P2|＝|y2－y1|.
两条平行线间的距离教学设计人教A版高中数学选择性必修第一册
一、情境导学前面我们已经得到了两点间的距离公式，点到直线的距离公式，关于平面上的距离问题，两条直线间的距离也是值得研究的。思考1：立定跳远测量的什么距离？A.两平行线的距离 B.点到直线的距离 C. 点到点的距离二、探究新知思考2：已知两条平行直线l_1,l_2的方程，如何求l_1 〖与l〗_2间的距离？根据两条平行直线间距离的含义，在直线l_1上取任一点P（x_0,y_0 ），,点P（x_0,y_0 ）到直线l_2的距离就是直线l_1与直线l_2间的距离，这样求两条平行线间的距离就转化为求点到直线的距离。两条平行直线间的距离1. 定义：夹在两平行线间的__________的长.公垂线段2. 图示： 3. 求法：转化为点到直线的距离.1．原点到直线x＋2y－5＝0的距离是( )A．2 B．3 C．2 D．5D [d＝|－5|12＋22＝5.选D.]
人教版高中数学选修3离散型随机变量及其分布列(1)教学设计
4.写出下列随机变量可能取的值，并说明随机变量所取的值表示的随机试验的结果．(1)一个袋中装有8个红球，3个白球，从中任取5个球，其中所含白球的个数为X.(2)一个袋中有5个同样大小的黑球，编号为1,2,3,4,5，从中任取3个球，取出的球的最大号码记为X.(3). 在本例(1)条件下，规定取出一个红球赢2元，而每取出一个白球输1元，以ξ表示赢得的钱数，结果如何？[解] (1)X可取0,1,2,3.X＝0表示取5个球全是红球；X＝1表示取1个白球，4个红球；X＝2表示取2个白球，3个红球；X＝3表示取3个白球，2个红球．(2)X可取3,4,5.X＝3表示取出的球编号为1,2,3；X＝4表示取出的球编号为1,2,4；1,3,4或2,3,4.X＝5表示取出的球编号为1,2,5；1,3,5；1,4,5；2,3,5；2,4,5或3,4,5.(3) ξ＝10表示取5个球全是红球；ξ＝7表示取1个白球，4个红球；ξ＝4表示取2个白球，3个红球；ξ＝1表示取3个白球，2个红球．
人教版高中数学选修3离散型随机变量的方差教学设计
3.下结论.依据均值和方差做出结论.跟踪训练2. A、B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析， X1和X2的分布列分别为X1 2% 8% 12% X2 5% 10%P 0.2 0.5 0.3 P 0.8 0.2求：(1)在A、B两个项目上各投资100万元， Y1和Y2分别表示投资项目A和B所获得的利润，求方差D(Y1)和D(Y2)；(2)根据得到的结论，对于投资者有什么建议？ 解：(1)题目可知，投资项目A和B所获得的利润Y1和Y2的分布列为：Y1 2 8 12 Y2 5 10P 0.2 0.5 0.3 P 0.8 0.2所以 ;; 解：(2) 由(1)可知 ，说明投资A项目比投资B项目期望收益要高；同时 ，说明投资A项目比投资B项目的实际收益相对于期望收益的平均波动要更大.因此，对于追求稳定的投资者，投资B项目更合适;而对于更看重利润并且愿意为了高利润承担风险的投资者，投资A项目更合适.
人教版高中数学选修3离散型随机变量的均值教学设计
对于离散型随机变量，可以由它的概率分布列确定与该随机变量相关事件的概率。但在实际问题中，有时我们更感兴趣的是随机变量的某些数字特征。例如，要了解某班同学在一次数学测验中的总体水平，很重要的是看平均分；要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。我们还常常希望直接通过数字来反映随机变量的某个方面的特征，最常用的有期望与方差.二、 探究新知探究1.甲乙两名射箭运动员射中目标靶的环数的分布列如下表所示：如何比较他们射箭水平的高低呢？环数X 7 8 9 10甲射中的概率 0.1 0.2 0.3 0.4乙射中的概率 0.15 0.25 0.4 0.2类似两组数据的比较,首先比较击中的平均环数,如果平均环数相等，再看稳定性.假设甲射箭n次，射中7环、8环、9环和10环的频率分别为：甲n次射箭射中的平均环数当n足够大时，频率稳定于概率，所以x稳定于7×0.1+8×0.2+9×0.3+10×0.4=9.即甲射中平均环数的稳定值(理论平均值)为9,这个平均值的大小可以反映甲运动员的射箭水平.同理，乙射中环数的平均值为7×0.15+8×0.25+9×0.4+10×0.2=8.65.
人教版高中数学选修3离散型随机变量及其分布列(2)教学设计
温故知新 1.离散型随机变量的定义可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量.通常用大写英文字母表示随机变量,例如X,Y,Z;用小写英文字母表示随机变量的取值,例如x,y,z.随机变量的特点: 试验之前可以判断其可能出现的所有值，在试验之前不可能确定取何值；可以用数字表示2、随机变量的分类①离散型随机变量:X的取值可一、一列出；②连续型随机变量:X可以取某个区间内的一切值随机变量将随机事件的结果数量化．3、古典概型:①试验中所有可能出现的基本事件只有有限个；②每个基本事件出现的可能性相等。二、探究新知探究1.抛掷一枚骰子,所得的点数X有哪些值？取每个值的概率是多少？ 因为X取值范围是{1，2，3，4，5，6}而且"P(X=m)"=1/6,m=1,2,3,4,5,6.因此X分布列如下表所示
人教部编版道德与法制四年级下册生活离不开他们说课稿
教学难点： 体会民风民俗对人们生活的影响，激发学生的民族自豪感。 教学准备1. 教师制作有关我国民风民俗的 PPT。2. 学生搜集传统节日的习俗、传说故事等资料。 教学过程一、导入新课 师：同学们，你们喜不喜欢放假？ 生：喜欢！师：那除了寒暑假，我们一般还会在什么情况放假？ 生：（各种回答）师：到了中国的传统节日的时候，我们也会放假。今天这节课我们就来学习与中国的传 统节日有关的民风民俗。 （揭示课题）二、认识春节1. 你知道我们中华民族有哪些传统节日？2. 春节的来历。3. 观看春节视频。4. 说一说，你们家是怎样过春节的?①过年前你们家会准备些什么？②除夕夜怎样辞旧迎新?③年初一怎样给长辈拜年？④你印象最深的一次春节是怎样的?三、猜一猜 春节的活动是如此多姿多彩，那你知道，人们最希望的过年方式是什么吗？出示教材内
婚礼秀策划方案
女一号（持麦）在烛火天使／伴娘的陪伴下于舷梯静候；男一号持麦（隐身会场）；悠扬小提琴开场；5秒后男一号爱的讲述（2分钟）并现身来宾中，穿越红地毯直达前台；灯光师追光扫射定格；伴奏音乐（月亮代表我的心）起；男一号深情演绎（2分22秒）；并缓行至红地毯三分之一处（第一台追光灯白光跟随），与些同时女一号在烛火天使引领和伴娘的陪伴下从舷梯步入会场至角亭内（第二台追光灯蓝光跟随）；男一号女一号爱的对白（1分钟）
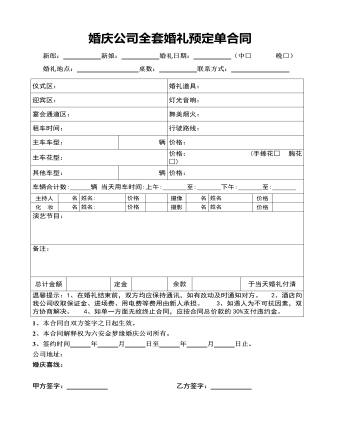
婚庆公司全套婚礼预定单合同
新郎： 新娘： 婚礼日期： （中□ 晚□）婚礼地点： 桌数： 联系方式： 仪式区： 婚礼道具：迎宾区： 灯光音响：宴会通道区： 舞美烟火：租车时间： 行驶路线：主车车型： 辆 价格：主车花型： 价格： (手捧花□ 胸花□)其他车型： 辆 价格：车辆合计数: 辆 当天用车时间:上午: 至: 下午: 至: 主持人 名 姓名: 价格 摄像 名 姓名 价格 化 妆 名 姓名: 价格 摄影 名 姓名 价格
《离子反应》说课稿
(二)教学目标 1.知识与技能目标：通过学习了解电离，电解质的概念;能用电离方程式表达常见、典型的电解质在水溶液中的电离，并从电离理论的角度认识酸、碱、盐;通过酸、碱、盐的本质探究，感悟科学探究的基本方法，提高科学探究能力。 2.过程与方法目标：培养学生通过实验探究问题，分析问题，归纳问题的能力。 3.情感态度与价值观目标：从更深的层面研究物质发生化学反应的意义，培养学生透过现象认识事物本质的能力。 (三)教学重难点 电解质的判断、电离及电离方程式的书写 二、说学情 对于高一年级年级的学生来说，他们虽然对化学基础知识有了一定积累，但程度参差不齐，差别较大，学生的抽象思维能力还有待进一步提高。这一年级的学生思维活跃，求知欲强，有强烈的好奇心，虽然处于抽象思维阶段，但本节概念比较抽象，应适当增加实验和电脑动画以使微观离子的.活动变得直观。
残疾人精准脱贫调研报告
1、落实工作责任，强化考核管理 始终坚持把残疾人脱贫攻坚放在突出位置来抓。在抓好各项帮扶措施落实的同时，努力细化目标，健全管理，强化责任，确保脱贫攻坚任务的如期完成。持续把残疾人小康建设纳入县委、县政府年度工作综合目标进行考核，强化各级、各相关单位做好残疾人脱贫攻坚的责任。将建档立卡残疾人帮扶任务分配到机关干部，进行一对一结对帮扶，要求帮扶工作有计划、有项目、有措施，坚持不脱贫不脱勾。在小康指标考核中，进一步突出残疾人之家创建、创业就业、低收入户脱贫、无障碍建设、精准康复等关键指标和重点任务的实现情况，使导向更加明确，发力更加精准。
精准扶贫调研报告
一是因病致贫是主因。在调查中了解到，雨霖村贫困户26户，其中因病因残致贫的16户，占贫困户的62%;缺劳力5户，占贫困户的19%。比如贫困户杨保炎患有重病，其子又有精神疾病，目前生活困难，无钱治病;贫困户王明平因病生活困难。 二是观念落后是根源。调查发现，贫困户绝大多数年龄偏大，文化程度不高，既无劳动力，又无技术，缺乏干事创业的激情，观念比较传统、保守，守摊子的思想比较突出。
《我准备?我成功》说课稿
三、班会程序设计：为了每个孩子都能在视、听、说、做、思等行为过程中经历学习的过程，顺利达成学习目标，我设计的教学程序如下：１、引生入境，导入新课，激发兴趣。首先播放课堂上的同学们因准备不足，拿课本，拿笔，找本子垫，找练习本，文具盒掉到地上的录像。让学生通过观看录像让学生找到自己的影子谈谈自己的认识，认识到课前准备的重要性。抛出问题：怎样才能让我们的课堂避免类似事情的发生呢？以此引出课题。这种以影片为先导与创设情境相结合的导课方式，可以抓住学生的注意力，激发学生的好奇心，启发学生的想象力，使学生产生浓厚的兴趣。２、观察欣赏、拓展思维、突出重点。紧接着图片展示，观看不同场景的图片。（第一种是书桌上学习用品杂乱的，第二种是课桌上干干静静的，第三种是课桌上整齐地摆放着下一节课要用到的学习用品的。）在出示图片的过程中教师可以适当的解说。
用空间向量研究距离、夹角问题（1）教学设计人教A版高中数学选择性必修第一册
二、探究新知一、点到直线的距离、两条平行直线之间的距离1.点到直线的距离已知直线l的单位方向向量为μ,A是直线l上的定点,P是直线l外一点.设(AP) ?=a,则向量(AP) ?在直线l上的投影向量(AQ) ?=(a·μ)μ.点P到直线l的距离为PQ=√(a^2 "-(" a"·" μ")" ^2 ).2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.点睛：点到直线的距离,即点到直线的垂线段的长度,由于直线与直线外一点确定一个平面,所以空间点到直线的距离问题可转化为空间某一个平面内点到直线的距离问题.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 . 答案: √174/6解析:如图,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),E(0,2,1),F(1,0,2),(EF) ?=(1,-2,1),
