-

人教版高中地理选修2三大自然区的内部差异教案
【知能训练】一、选择题(第1-5题为单项选择题,第6-7题为双项选择题)东北温带湿润、半湿润地区内的三江平原有“北大荒”之称,如今“北大荒”已被人们称为“北大仓”。据此完成1-2题:1、下列关于三江平原的叙述,正确的是()A.地处中温带湿润地区B.因粮食单位面积产量高而成为全国性的商品粮基地之一C.土壤因富含矿物质而形成肥沃的黑土D.夏季高温且雨热同期,利于冬小麦、玉米种植2、目前,三江平原还有大片沼泽荒地,但2000年国务院下令停止围垦,其主要原因是()A.我国已加入WTO,可以从国际市场大量廉价进口粮食B.保护“湿地”有利于改善生态环境C.开展多种经营,发展菱藕等水生植物生产D.煤、石油等矿产资源丰富,今后转向矿产资源开发利用3、我国西部地区的地理差异有()A.甘新多沙漠戈壁,青藏多大河湖泊B.陕甘宁地势低平,云贵川地形崎岖

人教版高中地理选修2实现双赢的能源战略—西气东输工程教案
图11-3 “西气东输线路示意图”图中可见西气东输工程主要穿越的地形区有塔里木盆地、河西走廊、宁夏平原、华北平原、长江中下游平原,连接了我国西部、中部和东部三个经济地带,自然景观上由东向西呈现出从沿海向内陆的地域分异。【教学内容】一、 打造中国能源输送的大动脉1、 西气东输工程概况(1)三大组成部分——天然气开发建设、主干管道建设、东部用户管网建设(2)主干道走向——西起新疆塔里木盆地的轮南油气田,向东经过库尔勒、吐鲁番、哈密、柳园、张掖、武威、干塘、中宁、靖边、柳林、郑州、尉氏、淮南、南京、常州,最终到达上海,全长近4200千米。[经典例题1]读“我国西气东输主干道走向示意图”(图11-5),回答:(1)天然气按形成和来源分属于来自 的能源,与煤炭相比具有的优点是

人教版高中地理选修2森林资源的合理利用与保护教案
1、图8.12“东北林区的分布”对照图例能够说出东北林区的三大分布区的名称、位置、森林类型及其主要树种。2、图8.13“东北平原西部的防护林分布”根据地图说出东北平原西部的防护林的位置、范围及其对生态环境的作用,并进而说出“三北防护林”的位置、范围及其对生态环境的作用。【教学内容】一、林业开发的现状与问题1、东北林区在我国林业中的地位(1)全国最大的林区:林地5000万公顷,占全国林地总面积的1/4上;人均林地超过0.5公顷,是全国人均林地的8倍,森林覆盖率36%,是全国平均数的3倍,木材蓄积量22.5亿立方米,占全国总量的1/3以上。(2)全国最大的木材基地:木材产量约占全国的40%。2、东北林区生产概况东北林区的森林采伐和制材工业发达,其中森林采伐业集中在大、小兴安岭和长白山三大林区。黑龙江省是我国最大的木材生产基地和最大的木材调出省。3、东北林区森林资源的分布

人教版高中地理选修2我国的三个经济地带教案
1、 下列四组地形中,全部属于西部大开发区域的是()A.江南丘陵——阿尔泰山——云贵高原——祁连山B.柴达木盆地——天山——江南丘陵——云贵高原C.准噶尔盆地——云贵高原——青藏高原——横断山D.塔里木盆地——云贵高原——黄土高原——太行山2、“西气东输”工程起始于()A.哈密盆地B.塔里木盆地C.柴达木盆地D.吐鲁番盆地3、 西部地区正在大力发展水电事业,其中已经建成并在最近开始向上海输送电能的水电站是()A.二滩水电站B.丹江口水电站C.龙羊峡水电站D.新安江水电站4、目前进入西藏地区主要依靠公路。下列四条进藏公路中,海拔最高的是()A.青藏公路B.川藏公路C.滇藏公路D.新藏公路5、青藏铁路将经过三江源(长江、黄河、澜沧江之源)地区。下列关于该地区地理环境特点的叙述,正确的是()A.山高坡陡,地势起伏大B.太阳辐射强,日照时间长,热量充足C.气温低,牧草矮,生态环境脆弱D.积雪冰川多,水资源和水能资源丰富

人教版高中地理选修3第二章第二节旅游资源开发条件的评价教案
案例①武夷山景区通过对案例①的学习,了解到:①武夷山景区自然景观优美,并具有较高的科学价值(丹霞地貌和生物多样性)、历史文化价值(丰富的文化遗存),具有极高的旅游资源价值。②地理位置优越和交通条件便利、基础设施完善。③武夷山的国内客源市场主要集中在长江三角洲和珠江三角洲,国际客源市场主要分布在以新加坡、日本为主的亚洲。游客多,市场广阔。通过分析,进一步了解旅游资源开发条件评价的基本内容。图2.15武夷山景区旅游略图通过图2.15了解了武夷山著名景区、景点的分布。活动根据案例,结合图2.15,试对武夷山景区的开发条件进行评价提示:可按以下步骤进行;1.根据学生各自的兴趣爱好和性格,自由组合分组。2.仔细阅读本案例,各组确定自己感兴趣的评价项目,并通过新闻媒介、网络、书籍等进一步收集有关信息。3.小组信息汇总,进行组内讨论。4.小组在全班进行汇报交流。

人教版高中地理选修3第二章第三节我国的旅游资源教案
2.对世界遗产的开发与保护原则——保护第一我国的世界文化遗产、世界文化与自然双遗产具有时代性、不可再生性和不可替代性,我国的世界自然遗产都代表着某一类地质地貌中最重要的历史演化过程,展示了我国独特的地质地貌和生物资源。世界遗产的开发与保护之间存在一定的矛盾。我们必须坚持保护第一的原则。旅游开发只是世界遗产的功用之一,必须十分慎重,做到保护与开发协调统一,不能造成对世界遗产的任何破坏。案例②我国第一个世界文化与自然双遗产——泰山通过学习案例②,了解到:①泰山不仅具有科学价值较高的地质构造,还具有多样的地貌景观,罕见的天象景观,丰富的生物资源。泰山自古以来即被誉为名山,受到皇家和百姓的顶礼膜拜,各朝各代几乎都进行过封禅行为,从而留下了深厚的历史文化遗存,这一点跟其他名山相比是独一无二的。

人教版高中地理选修3第三章第二节旅游景观欣赏的方法教案
【课标要求和解读】1.课标内容:举例说明旅游景观的观赏方法。活动建议——结合自己的旅游经历,交流欣赏旅游景观的体验。2.课标解读:要正确欣赏旅游资源,首先要以了解旅游资源的不同类型和景观特点为前提,并且对中外著名旅游景点有必要的了解;不同旅游景观形成原因不同,所以欣赏方法不同;了解欣赏旅游景观的主要方法——了解景观特点、选择合适的观察位置、把握有利的观察时机、洞悉景观的文化定位和历史内涵、激发健康的审美情趣。【教学目标和要求】1. 知识目标:明确旅游景观的描述和欣赏是多角度的,掌握不同景观的一般欣赏方法——了解景观特点、精选点位、把握时机、洞悉文化定位。2. 能力目标:初步学会不同的地文景观、气象景观、水域景观的正确的欣赏方法。3. 德育目标:培养审美情趣,提高审美素质;激发学生探索神奇大自然的兴趣;巩固学生热爱自然和祖国大好河山的感情。

人教版高中地理选修3第三章第一节旅游景观的审美特征教案
2.古建筑美:主要有城池、宫殿、陵墓、寺院、楼阁、桥、塔、民居等。古建筑美的形式主要表现在序列组合、空间安排、比例尺度、造型式样、色彩装饰等方面。3.自然景观中的人造景物(如民俗风情美、书画、雕塑艺术美等)在自然景观中,增加一些人造景物(人工美),如亭台楼阁、桥梁、寺庙等,本来是为了实用,如半山建亭,是为了游人途中休息,水上架桥是为了方便游览,但建造者按照美的规律,精心设计建造、精心装饰,有的还请著名书画家题写匾额楹联,使之不仅具有实用性,而且具有审美意义。它与自然景物形成一个统一的整体,构成绚丽多姿的风景美。图3.6城市雕塑图为位于兰州城南黄河之滨的巨型雕塑——《黄河母亲》。三、自然美与人工美的统一现今仍保持着原始形态的自然地域已经越来越少了。古今中外众多的自然景观都留有人工的痕迹。使这些人工痕迹与自然相映成趣,需要人们从和谐美的角度去巧妙安排。

人教版高中地理选修3第一章第二节旅游资源的类型教案
根据旅游资源的本质属性,通常将旅游资源划分为自然旅游资源和人文旅游资源两大类。(——此时将上述景观划分到这两类中去)我们凭直觉应该知道哪些是自然,哪些是人文旅游资源。那么两种资源是怎样定义与划分的呢?一、自然旅游资源与人文旅游资源P11与P12,两类资源。解释:一般而言,自然旅游资源以地貌景观为核心,人文旅游资源以建筑景观为核心。前者主要与各地的自然条件相关,后者主要与人类历史相关。但:有时,两类资源之间难以断定其归属,因为自然旅游资源的开发必须要经过人为的加工,不可能没有人文附加成分。而人类社会多数的创造,即使是最能体现人文色彩的民族风情,都与自然条件有密不可分的关系。两类资源又可细分为若干类,P11与P13阅读材料。

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。

北师大初中七年级数学上册比较线段的长短教案1
1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.(1)求线段MN的长;(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出MN的长度吗?请用简洁的话表达你发现的规律.

北师大初中七年级数学上册比较线段的长短教案2
教学反思: 1.本课时设计的主导思想是:将数形结合的思想渗透给学生,使学生对数与形有一个初步的认识.为将来的学习打下基础,这节课是一堂起始课,它为学生的思维开拓了一个新的天地.在传统的教学安排中,这节课的地位没有提到一定的高度,只是交给学生比较线段的方法,没有从数形结合的高度去认识.实际上这节课大有可讲,可以挖掘出较深的内容.在教知识的同时,交给学生一种很重要的数学思想.这一点不容忽视,在日常的教学中要时时注意.2.学生在小学时只会用圆规画圆,不会用圆规去度量线段的大小以及截取线段,通过这节课,学生对圆规的用法有一个新的认识.3.在课堂练习中安排了度量一些三角形的边的长度,目的是想通过度量使学生对“两点之间线段最短”这一结论有一个感性的认识,并为下面的教学做一个铺垫.

北师大初中七年级数学上册从三个方向看物体的形状教案1
1.经历从不同方向观察物体的活动过程,发展空间观念.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的形状.3.能识别从三个方向看到的简单物体的形状,会画立方体及简单组合体从三个方向看到的形状,并能根据看到的形状描述基本几何体或实物原型.一、情境导入观察图中不同方向拍摄的庐山美景.你能从苏东坡《题西林壁》诗句:“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”体验出其中的意境吗?你能挖掘出其中蕴含的数学道理吗?让我们一起探索新知吧!二、合作探究探究点一:从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的,从上面看到的平面图形是()解析:这个几何体从上面看,共有2行,第一行能看到3个小正方形,第二行能看到2个小正方形.故选D.
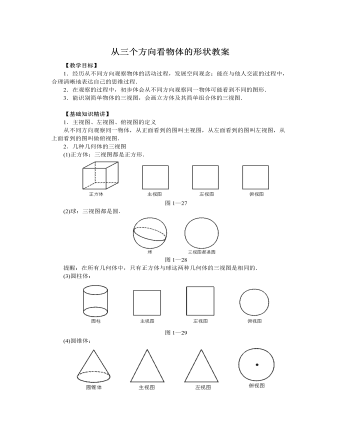
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中七年级数学上册代数式的求值教案1
(1)请你用代数式表示水渠的横断面面积;(2)计算当a=3,b=1时,水渠的横断面面积.解析:(1)根据梯形面积=12(上底+下底)×高,即可用含有a、b的代数式表示水渠横断面面积;(2)把a=3、b=1带入到(1)中求出的代数式中,其结果即为水渠的横断面面积.解:(1)∵梯形面积=12(上底+下底)×高,∴水渠的横断面面积为:12(a+b)b(m2);(2)当a=3,b=1时水渠的横断面面积为12(3+1)×1=2(m2).方法总结:解答本题时需搞清下列几个问题:(1)题目中给出的是什么图形?(2)这种图形的面积公式是什么?(3)根据公式求图形的面积需要知道哪几个量?(4)这些量是否已知或能求出?搞清楚了这些问题,求解就水到渠成.三、板书设计教学过程中,应通过活动使学生感知代数式运算在判断和推理上的意义,增强学生学习数学的兴趣,培养学生积极的情感和态度,为进一步学习奠定坚实的基础.

北师大初中七年级数学上册代数式的求值教案2
解 由题意可得,今年的年产值为a·(1+10%) 亿元,于是明年的年产值为a·(1+10%)·(1+10%)= 1.21a(亿元).若去年的年产值为2亿元,则明年的年产值为1.21a =1.21×2 = 2.42(亿元).答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以预计明年的年产值是2.42亿元.例3 当x=-3时,多项式mx3+nx-81的值是10,当x = 3时,求该代数式的值.解 当x=-3时,多项式mx3+nx-81=-27m-3n-81, 此时-27m-3n-81=10, 所以27m+3n=-91.则当x=3,mx3+nx-81 =( 27m+3n )-81=-91-81=-172.注:本题采用了一种重要的数学思想——“整体思想”.即是考虑问题时不是着眼于他的局部特征,而是把注意力和着眼点放在问题的整体结构上,把一些彼此独立,但实质上又相互紧密联系着的量作为整体来处理的思想方法.

北师大初中七年级数学上册等式的基本性质教案1
方法总结:对等式进行变形,必须在等式的两边同时进行,即同加或同减,同乘或同除,不能漏掉一边,且同加或同减,同乘或同除的数必须相同.探究点二:利用等式的基本性质解方程用等式的性质解下列方程:(1)4x+7=3; (2)12x-13x=4.解析:(1)在等式的两边都减7,再在等式的两边都除以4,可得答案;(2)在等式的两边都乘以6,再合并同类项,可得答案.解:(1)方程两边都减7,得4x=-4.方程两边都除以4,得x=-1;(2)方程两边都乘以6,得3x-2x=24,x=24.方法总结:解方程时,一般先将方程变形为ax=b的形式,然后再变形为x=c的形式.三、板书设计教学过程中,强调学生自主探索和合作交流,通过观察、操作、归纳等数学活动,感受数学思想的条理性和数学结论的严密性.

北师大初中七年级数学上册等式的基本性质教案2
教学目标1、知识目标:掌握等式的性质;会运用等式的性质解简单的一元一次方程。2、能力目标:通过观察、探究、归纳、应用,培养学生观察、分析、综合、抽象能力,获取学习数学的方法。3、情感目标:通过学生间的交流与合作,培养学生积极愉悦地参与数学学习活动的意识和情感,敢于面对数学活动中的困难,获得成功的体验,体会解决问题中与他人合作的重要性。教学重点与难点重点:理解和应用等式的性质。难点:应用等式的性质,把简单的一元一次方程化为“x=a”的形式。教学时数 2课时(本节课是第一课时)教学方法 多媒体教学教学过程(一) 创设情境,复习导入。上课开始,给出思考,(算一算,试一试)能否用估算法求出下列方程的解:(学生不用笔算,只能估算)

北师大初中七年级数学上册多边形和圆的初步认识教案1
方法总结:在分辨一个图形是否为多边形时,一定要抓住多边形定义中的关键词语,如“线段”“首尾顺次连接”“封闭”“平面图形”等.如此,对于某些似是而非的图形,只要根据定义进行对照和分析,即可判定.探究点二:确定多边形的对角线一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是()A.2015 B.2016 C.2017 D.2018解析:这个多边形的边数为2015+3=2018.故选D.方法总结:过n边形的一个顶点可以画出(n-3)条对角线.本题只要逆向求解即可.探究点三:求扇形圆心角将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,求这三个扇形圆心角的度数.解析:用扇形圆心角所对应的比去乘360°即可求出相应扇形圆心角的度数.解:三个扇形的圆心角度数分别为:360°×22+3+4=80°;360°×32+3+4=120°;

北师大初中七年级数学下册角平分线的性质教案
解析:根据AB∥CD,∠ACD=120°,得出∠CAB=60°.再根据尺规作图得出AM是∠CAB的平分线,即可得出∠MAB的度数.解:∵AB∥CD,∴∠ACD+∠CAB=180°.又∵∠ACD=120°,∴∠CAB=60°.由尺规作图知AM是∠CAB的平分线,∴∠MAB=12∠CAB=30°.方法总结:通过本题要掌握角平分线的作图步骤,根据作图明确AM是∠BAC的角平分线是解题的关键.三、板书设计1.角平分线的性质:角平分线上的点到这个角的两边的距离相等.2.角平分线的作法本节课由于采用了动手操作以及讨论交流等教学方法,从而有效地增强了学生对角以及角平分线的性质的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生在性质的运用上还存在问题,需要在今后的教学与作业中进一步的加强巩固和训练

