-

大班数学:看图填算式课件教案
2、幼儿会根据各种实物图片的内容列出算式。 3、培养幼儿语言表达能力。活动准备:实物图片若干张;分组活动的操作材料。活动过程: 一、开始部分: 1、复习顺数,按要求数数。(从4—13、17—29、56—65) 2、碰球游戏,复习9的分解组成。

计算活动:大班《数学宫》课件教案
2.训练思维的正确性、敏捷性。活动准备: 几何图形片10张、红黄蓝三色的几何图形板长方形、三角形、半圆形(上有红黑绿三种颜色写的1"10的数字各一个)、数字牌每人一块。活动过程: 师生进入数学宫 游戏一:做的对有快(复习10以内数的形成、数数)1. 目测几何图形的个数做动作

大班数学:做棒棒糖课件教案
活动准备:橡皮泥五块,玻璃纸五张(红、两色),木棒五根(四根粗,一根细),5以内加减卡片一套。活动过程:1、做棒糖:让孩子在规定的时间内将橡皮泥捏成球体状或正方体状,插上木棒后在包上玻璃纸(包出自己喜欢的式样)。2、数一数:自己做了几根棒糖?用了几块橡皮泥?几张玻璃纸?几根木棒?

大班数学活动:二等分课件教案
2、体会二等分给我们生活带来的便捷、美化作用。活动材料;教具:小蚂蚁两个、蛋糕一块、二等份图卡10张学具:长方形纸、剪刀、尺、毛线、包装纸;吸管、圆片、三角形、正方形;硬币、蚕豆、雪花片、纽扣、小碗;量杯6个、天平、蛋糕、番茄、豆腐干、刀子、菜板、橡皮泥等。活动过程:1、幼儿将长方形纸进行二等份。(1)班上请来了两位小客人,看看是谁?它们还带来了最喜欢吃的蛋糕,可是只有一块蛋糕,两人都想吃,怎么办?(2)请一位幼儿动手试一试,有什么办法知道这两块一样大呢?(重叠)(3)教师小结:把蛋糕分成一样大的两份,这种方法叫二等份。想想蛋糕除了这样分,还有不一样的分法吗?每位小朋友面前都有一张像蛋糕一样的长方形纸,请你想出和别人不同的方法进行二等份?

大班数学活动:5的加法课件教案
2、复习5的组成,并知道4 1、3 2及前后位置互换都等于5。 3、进一步认识理解“ ”、 “=”号的含义。 4、在活动中,体验游戏的愉悦,提高幼儿学习数学的兴趣。活动准备: 1、背景图一副,动物卡片若干。 2、教具:数量不等的物体图片,1—5数字,加、减、等号各一个。 3、学具:数量不等的物体图片(幼儿人手一份)。活动过程:(一)复习5的组成 幼儿人手一份卡片,教师引导一起共同复习5的组成。

中班数学:复习几何图形课件教案
2、让幼儿大胆想象,运用几何图形进行拼搭创造。活动准备:图形宝宝图片、背景图、固体胶、纸、环境布置活动重点:复习巩固对几何图形的认识活动难点:运用几何图形进行拼搭创造活动流程:引出课题 游戏巩固 活动延伸

中班数学:复习6的组成课件教案
2.积极参与讨论活动,大胆讲述自己的意见。活动准备:6的分合卡片,分类图一张。记录单、记号笔幼儿人手一份。 活动过程:1、复习5以内数的组成(1)游戏:碰球游戏前,由教师确定碰几球,如碰5球。教师问:“嗨,嗨,我的1球碰几球?”幼儿答:“嗨,嗨,我的1球碰4球?”速度可随着幼儿的熟练程度逐渐加快。游戏先集体后个人。

中班数学:《蜘蛛买鞋》课件教案
2、感受儿歌幽默有趣的语言风格。3、学习改变儿歌的数字并仿编新的诗句。 4、聆听音乐并用仿编的内容歌唱和表演活动准备:各种鞋及图卡数张、每人10枚硬币、每人一个小盒子。活动重点:学习10以内简单加减概念。活动难点:改变儿歌数字、并仿编新的诗句。活动过程:开始部分:问幼儿:小朋友你有几只脚?穿几只鞋?蜘蛛有几只脚?穿几鞋?基本部分:1 、教师和幼儿一起看屏幕,念儿歌《蜘蛛买鞋》念过一遍后,请幼儿再次念儿歌。同时拿出与鞋子等值的硬币、念到最后一句:"总共花了10元钱"时,请幼儿算算桌面上总共有多少钱,再作出答案。

中班数学:7是多少课件教案
准备 l~7数字卡片若干套,画有不同数目的图片若干套(两个小人;两件衣服;一个杯子、一顶帽子;3只鸭;一根蚊香、一瓶香水、一枝月季;一个苹果、一个香蕉、一对连枝樱桃、一块糖……)。

大班数学:猫捉老鼠课件教案
2、发展幼儿的灵敏性,培养幼儿良好的游戏秩序。活动准备:老鼠(背后有式题)、小猫头饰、拱形门、海洋球(球上贴有算式)、投球盒(盒上数字为1-10)、算式题(幼儿、老师都有)、彩旗(旗上有数字)、布置场景、铃鼓一只、雪花片活动过程:1.老师扮演猫妈妈,幼儿扮演猫宝宝师:宝宝们,今天妈妈带你们出去玩,好吗?来,坐上火车,出发啦!(火车音乐)进场后转一圈2.无意发现鼠迹师:呀,这里真漂亮,你们找个朋友玩一会儿吧! 宝宝,你们快来看哪,这里怎么乱七八糟,是谁干的呀?瞧,这里还有老鼠脚印呢!幼:老鼠

大班数学《5的组成》课件教案
2.能听口述应用题,在算盘上复习4以内的加减混合运算,并能完整说出算式。 3.在游戏和操作中练习看数拨珠,看珠报数。活动准备:1.苹果图及标记图,数卡1、2、3、4、5若干。 2.每人一张分合卡、一支记号笔、5个动物玩具。 3.四位数的电话号码若干。活动过程:1. 出示数卡5,今天数字5也到幼儿园来了,它说要到算盘上找到它的珠宝宝,你知道是哪颗珠宝宝吗? 幼儿回答,教师小结;哦,原来上珠宝宝就是5呀,那一颗下珠是几呀?三颗下珠呢?现在我们知道了,下珠宝宝1、2、3、4都比5小,现在数字5要来考考小朋友了,请你把5分成两份,看看谁的方法又多又准确。教师观察幼儿操作情况,并指导幼儿将分成结果记录在分合卡上。

人教版新目标初中英语七年级下册What does he look like教案3篇
所需要用到的句子:Who is that?That is Jack. I like him.Why do you like him?I like him because he is interesting.Task 4: 设计理想中的人类Step one: 设计理想中的人类的外貌。把全班同学分成若干小组,学生可以边说边在纸上画出他们的模样。Step two: 设计理想中人类的性格。学生们可以把那些能描述性格的单词写在图画的旁边。Step three: 每组选出一名同学,其他同组同学提问,他作简单回答,并说明原因。所需用到的句子:What does he or she look like?He or she ...What is he or she like?He or she is ...Why?Because ...Task 5: 挑战性活动调查性格是天生的还是后天形成的,让每个同学回家去调查一下自己成长过程中性格是否有变化,具体是怎样的,为什么会这样? Teaching Aims:1. Enable students to have a general understanding of how to talk about people's physical appearance.2. Enable students to tackle some essential vocabularies and patterns about describing people. Provide them with necessary skills and methods.3. Create various chances for students to describe the persons they're familiar with, such as classmates, family members, teachers, idols, etc.

北师大初中数学九年级上册利用三边判定三角形相似2教案
(一)导入新课三角形全等的判定中AA S 和ASA对应于相似三 角形的判定的判定定理1,SAS对应于相似三 角形的判定的判定定理2,那么SSS 对应的三角形相似的判定命题是否正确,这就是本节研究的内容.(板书)(二) 做一做画△ABC与△A′B′C′,使 、 和 都等 于给定的值k.(1)设法比较∠A与∠A′的大小;(2)△ABC与△A′B′C′相似吗?说说你的理由.改变k值的大小,再试一试.定理3:三边:成比例的两个三 角形相似.(三)例题学习例:如图,在△ABC和△ADE中,ABAD=BCDE=ACAE ,∠BAD=20°,求∠CAE的度数.解:∵ABAD=BCDE=ACAE ,∴△ABC∽△ADE(三边成比例的两个三角形相似). ∴∠BAC=∠DAE,∴∠BAC-∠DAC =∠D AE-∠DAC,即∠BAD=∠CAE.∵∠BAD=20°,∴∠CAE=20°. 三、巩固练习四、小结本节学 习了相似三角形的判定定理3,使用时一定要注意它使用的条件.

北师大初中数学九年级上册复杂图形的三视图2教案
教学目标:1.会画直棱柱(仅限于直三棱柱和直四棱柱)的三种视图,体会这几种几何体与其视图之间的相互转化。2. 会根据三视图描述原几何体。教学重点:掌握直棱柱的三视图的画法。能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法一、实物观察、空间想像观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过 想像,再抽象出这两个直棱柱的主视图,左视图和俯视图。绘制:请你将抽象出来的三种视图画出来,并与同伴交流。比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法。拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试。
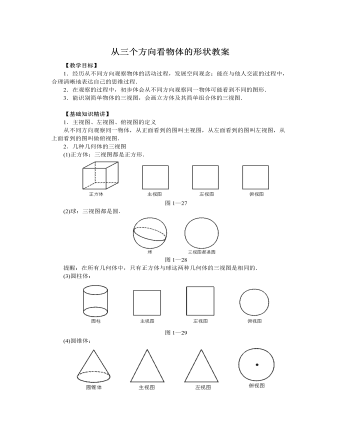
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中数学八年级上册三元一次方程组2教案
目的:课后作业设计包括了两个层面:作业1是为了巩固基础知识而设计;作业2是为了扩展学生的知识面;拓广知识,增加学生对数学问题本质的思考而设计,通过此题可让学生进一步运用三元一次方程组解决问题.教学设计反思1.本节课的内容属于选修学习的内容,主要突出对数学兴趣浓厚、学有余力的同学进一步探究和拓展使用,在数学方法和思想方面需重点引导,通过引导,使学生明白解多元方程组的一般方法和思想,理解巩固环节需多注意多种解题方法的引导,并且比较各种解题方法之间的优劣,总结出解多元方程的基本方法.2.作为选修课,在内容上要让学生理解三元一次方程组概念的同时,要让学生理解为什么要用三元一次方程组甚至多元方程组去求解实际问题的必要性,从而掌握本堂课的基础知识.在教学的过程中,要让学生充分理解对复杂的实际问题方程中元越多,等量关系的建立就越直接;充分理解代入消元法和加减法解方程的优点和缺点,有关这一方面的题目要让学生充分讨论、交流、合作,其理解才会深刻.

北师大初中数学八年级上册三角形的外角2教案
证法二:(1)延长BD交AC于E(或延长CD交AB于E),如图.则∠BDC是△CDE的一个外角.∴∠BDC>∠DEC.(三角形的一个外角大于任何一个和它不相邻的内角)∵∠DEC是△ABE的一个外角(已作)∴∠DEC>∠A(三角形的一个外角大于任何一个和它不相邻的内角)∴∠BDC>∠A(不等式的性质)(2)延长BD交AC于E,则∠BDC是△DCE的一个外角.∴∠BDC=∠C+∠DEC(三角形的一个外角等于和它不相邻的两个内角的和)∵∠DEC是△ABE的一个外角∴∠DEC=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和)∴∠BDC=∠B+∠C+∠BAC(等量代换)活动目的:让学生接触各种类型的几何证明题,提高逻辑推理能力,培养学生的证明思路,特别是不等关系的证明题,因为学生接触较少,因此更需要加强练习.注意事项:学生对于几何图形中的不等关系的证明比较陌生,因此有必要在证明第2小题中,要引导学生找到一个过渡角∠ACB,由∠1>∠ACB,∠ACB>∠2,再由不等关系的传递性得出∠1>∠2。

北师大初中数学九年级上册简单图形的三视图2教案
教学目标:1.经历由实物抽象出几何体的过程,进一步发展空间观念。2.会画圆柱、圆锥、球的三视图,体会这几种几何体与其视图之间的相互转化。3.会根据三视图描述原几何体。教学重点:掌握部分几何体的三视图的画法,能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法教学过程设计一、实物观察、空间想像设置:学生利用准备好的大小相同的正方形方块,搭建一个立体图形,让同学们画出三视图。而后,再要求学生利用手中12块正方形的方块实物,搭建2个立体图形,并画出它们的三视图。学生分小组合作交流、观察、作图。议一议1.图5-14中物体的形状分别可以看成什么样的几何体?从正面、侧面、上面看这些几何体,它们的形状各是什么样的?2.在图5-15中找出图5-14中各物体的主视图。3.图5-14中各物体的左视图是什么?俯视图呢?

北师大初中数学九年级上册利用两角判定三角形相似2教案
合探2 与同伴合作,两个人分别画△ABC和△A′B′ C′,使得∠A和∠A′都等于∠α,∠B和∠B′都等于∠β,此时,∠C与∠C′相等吗?三边的比 相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.四、导入定理判定 定理1:两角分别相等的两个三角形相似.这个定理的 出 现为判定两三角形相似增加了一条新的途径.例:如图,D ,E分别是△ABC的边AB,AC上的点,DE∥BC,AB= 7,AD=5,DE=10,求B C的长。解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC(两角分别相等的两 个三角形相似).∴ ADAB=DEBC.∴BC=AB×DEAD = 7×105=14.五、学生练习:1. 讨论随堂练 习第1题有一个锐角相等的两个直角三角形是否相似?为什么?2.自己独立完成随堂练习第2题六、小结本节主要学习了相似三角形的定义及相似三角形的判定定理1,一定要掌握好这个定理.七、作业:

北师大初中数学九年级上册利用相似三角形测高2教案
[想一想]同学们经历了上述三种方法,你还能想出哪些测量旗杆高度的方法?你认为最优化的方法是哪种?思路点拔:1、如果旗杆周围有足够地空地使旗杆在太阳光照射下影子都在平地上,并能测出影子的长度,那么,可以在平地垂直树一根小棒,等到小棒的影子恰好等于棒高时,再量旗杆的影子,此时旗杆的影子长度就是这个旗杆的高度.2、可以采用立一个已知长度的参照物在旗杆旁照相后量出照片中旗杆与参照物的长度根据线段成比例来进行计算.3、拿一根知道长度的直棒,手臂伸直,不断调整自己的位置,使直棒刚好完全挡住旗杆,量出此时人到旗杆的距离、人手臂的长度和棒长,就可以利用三角形相似来进行计算.等等.第四环节 课堂小结1、本节课你学到了哪些知识?2、在运用科学知识进行实践过程中,你是否想到最优的方法?3、在与同伴合作交流中,你对自己的表现满意吗?第五环节 布置作业,反思提炼

