-

XX年国旗下讲话稿:学会感恩
老师们、同学们:早上好!今天,我国旗下讲话的主题是《学会感恩》。有这样一个故事。一次,美国前总统罗斯福家失盗,被偷去了许多东西,一位朋友闻讯后,忙写信安慰他,劝他不必太在意。罗斯福给朋友写了一封回信:“亲爱的朋友,谢谢你来信安慰我,我现在很平安。感谢上帝:因为,贼偷去的是我的东西,而没有伤害我的生命;第二,贼只偷去我部分东西,而不是全部;第三,最值得庆幸的是,做贼的是他,而不是我。”对任何一个人来说,失盗绝对是不幸的事,而罗斯福却找出了感恩的三条理由。同学们,在家中,当你吃着可口的饭菜,你是否感恩父母付出的辛勤劳动?当你穿着漂亮暖和的衣服,你是否感恩父母对你的关心?也许有的同学会漠视这些来之不易的东西,父母们每天要在工作岗位上辛苦的工作十几个小时,他们付出了多少汗水?可面对父母语重心长的教诲,我们的孩子却无动于衷,会感到厌烦,甚至无礼地和父母顶撞。

年会个人代表发言讲话稿
在日常工作中用心努力地做好每件事,争取把问题想周到,尽量使自己能做到事半功倍的效果。在财务工作中我始终以提高工作效率和工作质量为目标,力争做到总公司和分公司财务制度统一,积极主动地了解各分公司财务工作中出现的问题,及时上报,及时解决。使得各分公司人员按照_总公司的制度和标准完成每项工作,熟练掌握工作流程,坚持按财务制度办事,保持头脑清醒,及时掌握各公司签订合同和收付工程款项等情况。在工作中发现问题,解决问题,采纳大家提出的合理化建议。

精编小学教师个人成长心得感悟收获八篇
一、教育教学方面本学年年初,我就给自己制定了继续把讲台站好、努力把讲台站活的大体目标,进而从备课、上课、课后反思三个环节着手对自己的教学工作进行改进。由于所教学生学习基础、学习习惯差别较大,这三个环节中我都努力做到因材施教,让成绩处于不同层面的学生都能有所进步。作为语文教师,我始终注重培养学生的写作能力,用文如其人的理念来感染和塑造他们的气质及人格。通过努力,我所教的班级语文成绩在年级名列前茅,辅导学生多次在报刊杂志上发表文章,并在多次作文比赛中获奖。

北师大初中数学九年级上册用因式分解法求解一元二次方程1教案
探究点二:选用适当的方法解一元二次方程用适当的方法解方程:(1)3x(x+5)=5(x+5);(2)3x2=4x+1;(3)5x2=4x-1.解:(1)原方程可变形为3x(x+5)-5(x+5)=0,即(x+5)(3x-5)=0,∴x+5=0或3x-5=0,∴x1=-5,x2=53;(2)将方程化为一般形式,得3x2-4x-1=0.这里a=3,b=-4,c=-1,∴b2-4ac=(-4)2-4×3×(-1)=28>0,∴x=4±282×3=4±276=2±73,∴x1=2+73,x2=2-73;(3)将方程化为一般形式,得5x2-4x+1=0.这里a=5,b=-4,c=1,∴b2-4ac=(-4)2-4×5×1=-4<0,∴原方程没有实数根.方法总结:解一元二次方程时,若没有具体的要求,应尽量选择最简便的方法去解,能用因式分解法或直接开平方法的选用因式分解法或直接开平方法;若不能用上述方法,可用公式法求解.在用公式法时,要先计算b2-4ac的值,若b2-4ac<0,则判断原方程没有实数根.没有特殊要求时,一般不用配方法.

北师大初中数学九年级上册用因式分解法求解一元二次方程2教案
【学习目标】1 、学习过程与方法:因式分解法是把一个一元二次方程化为两个一元一次方程来解,体现了一种“降次”思想、“转化”思想,并了解这种转化思想在解方程中的应用。2、学习重点 :用因式分解法解某些方程。 【温故】1、(1)将一个多项式(特别是二次三项式)因式分解,有哪几种分解方法?(2)将下列多项式因式分解① 3x2-4x ② 4x2-9y2 ③x2- 6xy+9y2④ (2x+1)2+4(2x+1)+4 【知新】1.自学课本 P46----P48[讨论]以上解方程的方法是如何使二次方程降为一次的?2、用分解因式法 解方程例1、解下 列方程(1)3 x2-5x=0 (2)x(x-2) +x-2=0例2、用因式分解法解下列方程 (1)5x2-2x-1/4=x2-2x+3/4 (2)x(x-3)-4( 3-x)=0 (3)(5-x)2-16=0 (4)16(2x-1)2=25(x-2)2

北师大初中数学九年级上册用配方法求解简单的一元二次方程1教案
探究点二:用配方法解二次项系数为1的一元二次方程用配方法解方程:x2+2x-1=0.解析:方程左边不是一个完全平方式,需将左边配方.解:移项,得x2+2x=1.配方,得x2+2x+(22)2=1+(22)2,即(x+1)2=2.开平方,得x+1=±2.解得x1=2-1,x2=-2-1.方法总结:用配方法解一元二次方程时,应按照步骤严格进行,以免出错.配方添加时,记住方程左右两边同时加上一次项系数一半的平方.三、板书设计用配方法解简单的一元二次方程:1.直接开平方法:形如(x+m)2=n(n≥0)用直接开平方法解.2.用配方法解一元二次方程的基本思路是将方程转化为(x+m)2=n(n≥0)的形式,再用直接开平方法,便可求出它的根.3.用配方法解二次项系数为1的一元二次方程的一般步骤:(1)移项,把方程的常数项移到方程的右边,使方程的左边只含二次项和一次项;(2)配方,方程两边都加上一次项系数一半的平方,把原方程化为(x+m)2=n(n≥0)的形式;(3)用直接开平方法求出它的解.

北师大初中数学九年级上册用配方法求解简单的一元二次方程2教案
(1) 你能解哪些特殊的一元二次方程?(2) 你会解下列一元二次方程吗?你是怎么做的?x2=5,2x2+3=5,x2+2x+1=5 ,(x+6)2 +72 = 102(3) 你能解方程x2+12x-15=0吗?你遇到的困难是什么?你能设法将这个方程转化成上面方程的形式吗?与同伴进行交流。活动二:做一做:填上适当的数,使下列等式成立(1)x2+12x+ =(x+6)2 (2)x2―4x+ =(x― )2 (3)x2+8x+ =(x+ )2 在上面等式的左边,常数项和一次项有什么关系解一元二次方程的思路是什么?活动三:例1、解方程:x2+8x-9=0你能用语言总结配方法吗?课本37页随堂练习课时作业:

北师大初中数学九年级上册用配方法求解简单的一元二次方程2教案
二、合作交流活动一:(1) 你能解哪些特殊的一元二次方程?(2) 你会解下列一元二次方程吗?你是怎么做的?x2=5,2x2+3=5,x2+2x+1=5 ,(x+6)2 +72 = 102(3) 你能解方程x2+12x-15=0吗?你遇到的困难是什么?你能设法将这个方程转化成上面方程的形式吗?与同伴进行交流。活动二:做一做:填上适当的数,使下列等式成立(1)x2+12x+ =(x+6)2 (2)x2―4x+ =(x― )2 (3)x2+8x+ =(x+ )2 在上面等式的左边,常数项和一次项有什么关系解一元二次方程的思路是什么?活动三:例1、解方程:x2+8x-9=0你能用语言总结配方法吗?课本37页随堂练习课时作业:

北师大初中数学九年级上册用因式分解法求解一元二次方程2教案
【学习目标】1 、学习过程与方法:因式分解法是把一个一元二次方程化为两个一元一次方程来解,体现了一种“降次”思想、“转化”思想,并了解这种转化思想在解方程中的应用。2、学习重点 :用因式分解法解某些方程。 【温故】1、(1)将一个多项式(特别是二次三项式)因式分解,有哪几种分解方法?(2)将下列多项式因式分解① 3x2-4x ② 4x2-9y2 ③x2- 6xy+9y2④ (2x+1)2+4(2x+1)+4 【知新】1.自学课本 P46----P48[讨论]以上解方程的方法是如何使二次方程降为一次的?2、用分解因式法 解方程例1、解下 列方程(1)3 x2-5x=0 (2)x(x-2) +x-2=0例2、用因式分解法解下列方程 (1)5x2-2x-1/4=x2-2x+3/4 (2)x(x-3)-4( 3-x)=0 (3)(5-x)2-16=0 (4)16(2x-1)2=25(x-2)2

人教版新课标高中地理必修2第二章第一节城市内部空间结构教案
为城市居民提供休养生息的场所,是城市最基本的功能区.城市中最为广泛的土地利用方式就是住宅用地.一般住宅区占据城市空间的40%—60%。(阅读图2.3)请同学讲解高级住宅区与低级住宅区的差别(学生答)(教师总结)(教师讲解)另外还有行政区、文化区等。而在中小城市,这些部门占地面积很小,或者布局分散,形成不了相应的功能 区。(教师提问)我们把城市功能区分了好几种,比如说住宅区,是不是土地都是被居住地占据呢?是不是就没有其他的功能了呢?(学生回答)不是(教师总结)不是的。我们说的住宅区只是在占地面积上,它是占绝大多数,但还是有土地是被其它功能占据的,比如说住宅区里的商店、绿化等也要占据一定的土地, 只是占的比例比较小而已。下面请看书上的活动题。
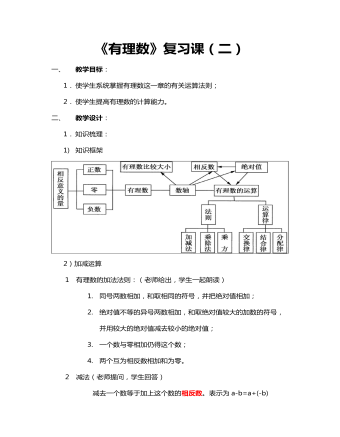
有理数复习教案教学设计
3)乘除运算①有理数的乘法法则:(老师给出,学生一起朗读)1. 两数相乘,同号得正,异号得负,并把绝对值相乘;2. 任何数与零相乘都得零;3. 几个不等于零的数相乘,积的符号由负因数的个数决定,当负因数有奇数个数,积为负;当负因数的个数为偶数个时,积为正;4. 几个有理数相乘,若其中有一个为零,积就为零。②有理数的除法法则:(老师提问,学生回答)1. 两个有理数相除,同号得正,异号得负,并把绝对值相除;2. 除以一个数等于乘以这个数的倒数。③关系(老师给出)除法转化为乘法进行运算。

有关公司年度工作计划
一、完善公司组织架构由于大量的人才引入和公司办公区域的扩展,公司的组织架构也就相应的随之改变。组织架构建设也决定着企业的发展方向。在XX年首先应协助领导完成公司组织架构的完善。确定和区分每个职能部门的权责,使每个部门责权明确,让员工清晰地知道自己的岗位责任、工作内容、工作权限、工作条件、必备的岗位技能及与相关岗位的汇报与负责关系等,真正做到组织架构的科学适用,保证公司的运营在既有的组织架构中良好、规范的发展

大班科学教案:有趣的汁液
2、操作工具:塑料袋、剪刀、盘子、纱布、小铁锤、小木棍、抹布、棉签、图画纸、宣纸等。3、师用教具:隐形画范图一幅、电炉一个活动过程:一、引入导语:春天到了,春姑娘给我们送礼物来了。讨论:为什么你们觉得鲜花很漂亮?五颜六色的鲜花有什么用?小结:鲜花能美化环境,鲜花的汁液能绘画、染纸。二、幼儿进行尝试活动1、尝试活动⑴:导语:既然花汁能染纸,那花汁是怎样取得的呢?幼儿讨论并进行尝试活动(挤汁--染纸)2、尝试活动⑵:导语:春姑娘不仅给我们送来了鲜花,还送来了丰富的水果,水果除了好吃以外,它能画画吗?幼儿讨论并进行尝试活动(挤汁---用棉签沾果汁在图画纸上作画)小结:果汁能画画,但有的果汁干了以后,就什么也看不见。

大班科学教案:有趣的转动
二、活动目标、重难点 1、在操作活动中,让幼儿获得物体转动的感性经验,培养幼儿对科学活动的兴趣。 2、培养幼儿对“转动”这一科学现象的兴趣,并在操作、引导幼儿获得物体转动的相关经验。 3、体验物体转动的乐趣,初步感受现代科技给人们带来的方便。 这是一堂科学课,主要培养幼儿对科学活动感兴趣,其中提供了日常常见的物体让幼儿进行探索,设计了课件让幼儿能直观的欣赏,这样可以加深幼儿的印象,因此整堂课重点就在于让幼儿对物体的转动有初步的了解并获得物体转动的相关经验,而作为难点,是让幼儿自己去动手发现物体是怎样在转动的原理。

大班科学教案:有趣的叶子
活动准备: 带幼儿参观植物园或附近的公园,收集落叶。 录音机、音乐磁带,线、纸条、双面胶等。活动目标:1、发展幼儿的观察能力并体验游戏带来的快乐。2、激发幼儿想象,创编叶子飞舞的动作并用肢体动作来表现音乐。 活动过程: 一、观察、接触各种植物的叶子: (把幼儿分成三组,每组摆放一篮叶子供幼儿自由选择)1、观察叶子的形状及颜色。教师:“你们发现了什么?这些叶子都一样吗?”给幼儿自由谈论的时间,相互交流、分享经验。2、鼓励幼儿大胆想象叶子的形状像什么?同时让幼儿在白板上用线条画出叶子的轮廓,进一步熟悉叶子的外型。3、发展幼儿的动手能力,串叶子,做挂饰。每个幼儿拿一片自己喜欢的叶子固定在纸条或线上,挂在脖子上。

大班科学教案:有趣的头发
[活动准备]1、不同大小重量的瓶子(装饰成不同大小的鱼)、筐。2、各种颜色的假发,图片若干。3、人手一盒操作材料。4、绿发娃娃、剪刀、辫线、可乐瓶娃娃、橡皮泥、乒乓球、笔。 [活动过程] 一、游戏“钓鱼”,激发幼儿兴趣。 请幼儿上来逐一从小大到玩“钓鱼”的游戏,当鱼线断了后,组织幼儿讨论:为什么会断?看看钓鱼线是用什么做的? 幼儿讨论,教师小结:头发受到过大的拉力,就会断的。

大班科学教案:影子真有趣
[活动准备] (1)活动前几天就有意识地让孩子观察物体的影子。 (2)室内布置的暗一些,准备多媒体大屏幕、简单的背景图。 (3)部分小动物或蔬菜、水果等玩具(塑料的或绒布的)以及透明的玻璃片、饮料瓶等。 (4)手电筒、简单的背景图。[活动过程] 一、说说:生活中见到的影子 1、师:我的手能变出各种小动物,请你看着它的影子,猜猜它是谁? 2、(猜猜老师的手影,在强光下变化出不同的形象)让孩子们尽情地猜一下“它是谁”?你还能用自己的小手变出什么吗?来试试看?(给孩子机会,让他大胆尝试) 3、扩散思维: (1)、师:“刚才你看到的是我们手的影子,除了这些你还见到过谁的影子呢”?(尽量调动每个幼儿的已有经验,大胆地讲出自己观察到的各种各样的影子) (2)、大树的影子是什么样子的?你想怎么来表示?小狗的呢?小花的呢……?)”(这里把主动权交给孩子,让他们发挥想象力、表现力以及语言表达能力)

大班美术教案:有趣的喷画
活动准备: 1、幼儿利用光线做影子游戏。 2、1—4种调好的颜料;每人2只吸管或1把牙刷、一块纱布;擦手布。活动过程:a) 出示喷画范例:小象的影子,引起幼儿的学画兴趣。 老师:画上是什么动物?画的前面没有光也没有小象,小象的影子怎么会到纸上呢?

大班美术教案:《有趣的圆形》
二、活动准备:彩笔 画纸 投影仪 圆形教具(特制) (两个圆形虚线处缝合,再在圆形的面上绘图。教师演示时要快,像是变魔术,幼儿会很感兴趣。)三、活动过程:1、 以《洋娃娃和小熊跳舞》的舞蹈进入活动场地,以手形游戏导入课题,调动幼儿学习兴趣。2、 以孙悟空七十二变的本领,激发幼儿想像力和创造力,想象出于圆形相象的物体。3、 通过幼儿书空添画和投影添画,引导幼儿举一反三,进行其它几何图形变通思维,构画出与其相象的物体,激发幼儿绘画欲望。

大班主题教案:有趣的叶子
活动准备: 1、带幼儿参观植物园或附近的公园,收集落叶。 2、录音机、音乐磁带,线、纸条、双面胶等。 活动过程: 一、观察、接触各种植物的叶子: (把幼儿分成三组,每组摆放一篮叶子供幼儿自由选择) 1、观察叶子的形状及颜色。教师:“你们发现了什么?这些叶子都一样吗?”给幼儿自由谈论的时间,相互交流、分享经验。 2、鼓励幼儿大胆想象叶子的形状像什么?同时让幼儿在白板上用线条画出叶子的轮廓,进一步熟悉叶子的外型。 3、发展幼儿的动手能力,串叶子,做挂饰。每个幼儿拿一片自己喜欢的叶子固定在纸条或线上,挂在脖子上。

