-
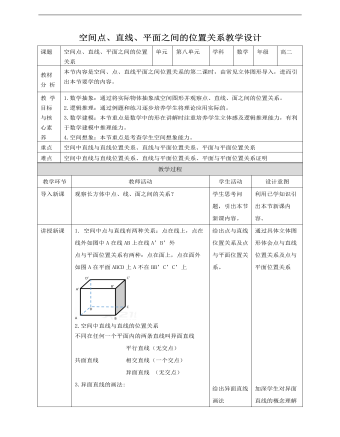
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.

人教A版高中数学必修一正弦函数、余弦函数的图像教学设计(2)
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系. 数学学科素养1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

在2023年国企第一批主题教育经验做法总结深化推进会上的讲话
检视整改,从字面上理解,包括两层含义,一是检视,就是查摆问题,分析原因,明确努力方向;二是整改,就是聚焦问题,靶向治疗,纠正工作偏差。这次主题教育检视整改形成了一些好机制。检视整改与其他重点措施有机融合、相互贯通。一个突出表现就是要求领导干部把调研发现的问题与推动发展遇到的问题、群众反映强烈的问题以及巡视巡察、审计监督等暴露的问题,一并列出问题清单进行整改,这既体现了边学习、边对照、边检视、边整改的要求,也有效解决了调查研究与检视整改相脱节的问题。开展性分析要求明确、特色鲜明。开展性分析,是严肃内政治生活的一项经常性工作。的十八届六中全会通过的《关于新形势下内政治生活的若干准则》中明确,“督促员对照章规定的员标准、对照入誓词、联系个人实际进行性分析”。

在学习贯彻主题教育动员部署会上的总结讲话
所属单位机关部门D组织ZT教育可以适当错后启动,拉开时间梯次,但也不能与上级单位间隔时间过长,最晚5月5日前要全面启动。需要强调的是,不管什么时间启动,具体到每个单位、部门,开展ZT教育的时间都不能少于5个月。无论采取哪种方式启动,都要讲清这次ZT教育的重大意义、目标要求、工作安排等。总公司机关各部门、所属各单位、各化工公司要将启动方案报巡回指导组审阅把关,巡回指导组还要现场参加指导各部门、各单位的启动工作。三、高水平进行ZT教育督促指导。强有力的督促指导是搞好ZT教育的重要保证,要把严督实导贯穿指导开展ZT教育全过程。按照D中央要求,总公司所属各单位不再派出指导组。这对总公司巡回指导组来说,担子更重了,既要直接指导所属各单位和化工公司本级D委,又要延伸指导所属单位机关部门、直属单位D组织。

在学习贯彻主题教育动员部署会上的总结讲话
无论采取哪种方式启动,都要讲清这次ZT教育的重大意义、目标要求、工作安排等。总公司机关各部门、所属各单位、各化工公司要将启动方案报巡回指导组审阅把关,巡回指导组还要现场参加指导各部门、各单位的启动工作。三、高水平进行ZT教育督促指导。强有力的督促指导是搞好ZT教育的重要保证,要把严督实导贯穿指导开展ZT教育全过程。按照D中央要求,总公司所属各单位不再派出指导组。这对总公司巡回指导组来说,担子更重了,既要直接指导所属各单位和化工公司本级D委,又要延伸指导所属单位机关部门、直属单位D组织。要把准巡回指导工作定位,切实尊重各单位D委主体地位,紧紧依靠他们开展工作,既指出存在问题又要帮助研究对策,真正实现同题共答。

劳动合同的种类
1、录用合同,它是指用人单位在国家劳动部门下达的劳动指标内,通过公开招收、择优录用的方式订立的劳动合同。录用合同一般适用于招收普通劳动者。目前,全民所有制企业、国家机关、事业单位、社会团体等用人单位招收录用劳动合同的特点是:用人单位按照预先规定的条件,面向社会,公开招收劳动者;应招者根据用人单位公布的条件,自愿报名;用人单位全面考核、择优录用劳动者;双方签订劳动合同。

司机的劳动合同
四、公司承诺1、来自外地招聘的驾驶员,在本岗位工作满三个月,路费凭票证可以实报实销;2、公司提供驾驶员住宿条件(包括水、电、暖、床、空调、卫生间设施);3、试用期驾驶员一经正式录用,驾驶员行驶在货运途中,伙食补贴为每天50元;4、电话费为每辆车每月100元。

业务员的劳动合同
(一)乙方实行以下第种工时制。1、实行固定工作制的,平均每日工作时间不得超过8小时,平均每周工作时间不得超过60小时。2、实行不定时工作制的,工作时间和休息休假甲乙双方协商安排。(二)甲方因工作需要安排延长乙方工作时间的,应依法安排乙方同等时间补休或支付加班加点工资。(注:加班加点工资标准应按国家相关规定明示于合同中。)(三)乙方依法享受国家规定的节假日和本单位规定休假制度。注:工作时间和休息休假是《劳动合同法》新增的必备条款。第四条劳动保护和劳动条件(一)甲方根据生产岗位的需要,按照国家有关劳动安全、卫生的规定为乙方配备必要安全防护措施,发放必要的劳动保护用品。(二)甲方根据国家有关法律、法规,建立安全生产制度;乙方应当严格遵守甲方的劳动安全制度,严禁违章作业,防止劳动过程中的事故,减少职业危害。

离婚协议的签订
二、办理协议离婚必须符合的条件1、当事人双方须有自愿离婚的合意,且意思表示真实;2.当事人须对子女和财产作适当处理;3、办理过结婚登记;4.双方当事人具有完全民事行为能力。三、双方自愿离婚的程序 根据《婚姻法》和《婚姻登记管理条例》的规定,男女双方自愿离婚,必须到婚姻登记机关办理离婚登记(婚姻登记机关,在农村是乡、民族乡、镇人民政府,在城市是街道办事处和市辖区的民政部门或者不设区的市人民政府的民政部门).其程序如下:

街道的工作总结
社会保障不断完善。城乡居民社会养老保险、城乡居民基本医疗保险实现全覆盖。城乡居民基本养老保险续缴1667人,续缴率99%;职工养老保险扩面净增1700人,完成任务的101%;城乡居民合作医疗参保34044人,参合率达99.54%。合作医疗基金补偿38.1万人次,补偿金额达3517万元。

药具的工作总结
为鼓励和引导广大育龄群众自觉自愿的使用药具避孕,减轻使用人员的心理负担,上半年我镇广泛开展了药具公开服务承诺活动,主要从以下六个方面开展了大量工作:

《蝴蝶的家》说课稿
课前播放凯丽金的名曲《回家》,配以一家人在家中其乐融融的图片,欣赏着熟悉而温馨的场景,倾听着优美动听的旋律,学生心是暖暖的,图片将学生的目光由人的家引向了其它生灵的家,蜜蜂有蜜蜂的家,小鸟有小鸟的家,那么蝴蝶的家在哪儿呢?此时,学生带着疑问兴趣盎然地走进了文本。

《爬山虎的脚》说课稿
叶圣陶爷爷还观察到了叶子颜色的变化,叶子的颜色是怎么变化的?(嫩红的→嫩绿的→绿得很新鲜)叶子的颜色变化也很美啊,谁能读出这种美来?老师为你们配上音乐和爬山虎的图片,能读得更美吗?

《朱德的扁担》说课稿
出示朱德挑粮画面,让学生说说看到的朱德,培养学生的语言表达能力,并从说中感悟挑粮的多、沉、重,体会朱德挑粮的艰辛。

《搭船的鸟》说课稿
利用课件向学生展示一些人与动物和谐共处,互相亲近的图片供学生欣赏生自由谈观后感。“一只翠鸟搭上了一位小朋友的船,他要干什么呢?小朋友心里是怎样想的呢?让我们快去课文里看看吧!”板书课题(搭船的鸟)。




